bayes学习笔记

贝叶斯（BAYES）判别思想是根据先验概率求出后验概率，并依据后验概率分布作出统计推断。所谓先验概率,就是用概率来描述人们事先对所研究的对象的认识的程度；所谓后验概率，就是根据具体资料、先验概率、特定的判别规则所计算出来的概率。它是对先验概率修正后的结果。

为什么是对一个新的实例进行分类的时候总是由其最大后验概率进行分类呢？

后验概率最大化的含义：

朴素贝叶斯法将实例分到后验概率最大的类中，这等价于期望风险最小化。假设选择0-1损失函数：

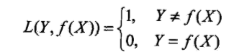
式中是分类决策函数，这时，期望风险函数为

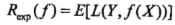
期望是对联合分布P（X，Y）取的。由此取条件期望

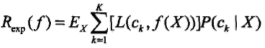
为了使期望风险最小化，只需对 X = x 逐个极小化，由此得到:

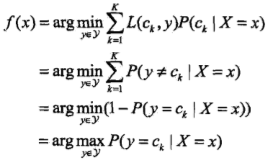
这样一来，根据期望风险最小化准则就得到了后验概率最大化准则：

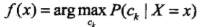
即朴素贝叶斯法所采用的原理

其中先验概率和条件分布采用的是极大似然估计的方法进行计算

极大似然估计：它是建立在极大似然原理的基础上的一个统计方法，极大似然原理的直观想法是，一个随机试验如有若干个可能的结果A，B，C，... ，若在一次试验中，结果A出现了，那么可以认为实验条件对A的出现有利，也即出现的概率P(A)较大。

朴素贝叶斯优化的方法：拉普拉斯平滑

为什么要进行平滑处理？

零概率问题，就是在计算实例的概率时，如果某个量x，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0。在文本分类的问题中，当一个词语没有在训练样本中出现，该词语调概率为0，使用连乘计算文本出现概率时也为0。这是不合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0。

拉普拉斯的理论支撑：

为了解决零概率的问题，法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。
假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。

拉普拉斯修正避免了因训练集样本不充分而导致概率估计值为零的问题，并且在训练集变大时，修正过程引入的先验的影响也会逐渐变得可忽略，使得估值渐趋向于实际概率值