插头DP学习笔记

插头DP（我也不知道该怎么定义...）是一种类似于洛谷题目（【模板】插头DP）的题目

题目特征为：

• 在棋盘上
• 某一维的数据范围很小
• 完全铺满
• 计数问题

直接看题吧。

【模板】插头DP

给出n*m的方格，有些格子不能铺线，其它格子必须铺，形成一个闭合回路。问有多少种铺法？(2<=n,m<=12)

考虑依次枚举每一个格子，存储轮廓线的状态。

例如图中我们当前正在考虑转移橙色格子，那么轮廓线就是图中的红线。

我们存储轮廓线上的插头。什么是插头呢？

例如下图

本图中的连线在轮廓线上的相交处就是所谓的插头。由于同一个连通块一定是联通的，在轮廓线上一定有两个交点，所以我们用左插头和右插头来表示这个插头是一个轮廓线的左侧交点还是右侧交点。显然两个连通块不可能相交，所以我们用括号序的形式来呈现左插头和右插头。如果我们以左插头为1，右插头为2，没有插头为0，则上图中的轮廓线插头状态是1201122。由于同一种方案在轮廓线上插头一定是一样的，而当前的转移至于轮廓线上的插头有关，符合DP的条件，所以我们可以存储以每一种轮廓线上插头的形式为下标，方案数为值的DP数组，依次考虑每一格子的插头形态，转移轮廓线。

注意为了后面讲解方便，我将连通块用同时用两种颜色标记，表示内部和外部。

显然这个格子的转移只与两条边有关：如图标记的两条黑边

根据这个格子附近的轮廓线情况，我们有若干种转移：

（以下图中轮廓线上方的插头情况仅供参考，实际可能有很多种情况，但是由于我们只考虑轮廓线上的插头，这几种情况本质上是一样的）

图太小了，凑合着看吧。。。

0.障碍节点

障碍节点不能防止插头，只有L=0&&R=0才能转移。

下面是非障碍节点的情况。

1.L=0, R=0

由于必须要放置插头，所以我们在下方放置一个左插头，右方放置一个右插头，即变成L=1 R=2

2.L=1, R=2

显然的是，我们可以补充一个左插头和一个右插头来形成一个回路。但是由于题目中要求只能形成一个闭合回路，所以如果当前考虑的节点是最后一个可以转移的非障碍节点，我们即可计入最终答案，否则不处理.

3.L=2, R=1

这次我们可以直接补充一个右插头和一个左插头来使得这两个回路形成一个回路。新的轮廓线上即变为L=0 R=0

4.L=1, R=1

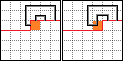
显然我们需要把两个连通块连接在一起，但是我们需要更改和R连接的插头的方向，如图。我们找到和上方插头匹配的右插头，将其变更为左插头即可。实际写代码可能稍微麻烦一点。

5.L=2, R=2

和上一种情况类似，只是对称过来了，我们需要向左找和左方插头匹配的左插头，将其变更为右插头。

6.L!=0, R=0

我们只需要延伸这个插头：向下或向右，即L=原L,R=0或L=0,R=原L

7.L!=0, R=0

和上一种情况类似，我们只需要延伸插头。

然后我们可以写代码了。由于状压每个位置有3种状态，我们需要3进制。由于3进制太麻烦了，所以我们用4进制。所以状态编号复杂度为\(4^{12+1}\)，大概六千万多，显然存不下，需要哈希表。这里偷懒使用unordered_map，在洛谷上不开O2刚好能过。

#include <bits/stdc++.h>
using namespace std;

int main()
{
	int n, m;
	bool chenge[15][15];
	char ch;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			scanf(" %c", &ch), chenge[i][j] = (ch == '*');
	unordered_map<int, long long> mp[2];
	mp[0][0] = 1;
	long long ans = 0;
	int nn = -1, mm = -1;
	for (int i = n; i >= 1; i--)
		for (int j = m; j >= 1; j--)
			if (chenge[i][j] != 1)
			{
				nn = i, mm = j;
				goto fuck;
			}
	fuck:
	if (nn == -1 && mm == -1)
	{
		printf("0\n");
		return 0;
	}
	int tot = (1 << (2 * m)) - 1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			mp[1].clear();
			for (pair<const int, long long> &cjh : mp[0])
			{
				int s = cjh.first;
				int L = (s >> (j * 2 - 2)) & 3, R = (s >> (j * 2)) & 3;
				int src = s;
				s ^= (L << (j * 2 - 2));
				s ^= (R << (j * 2));
				if (chenge[i][j] == 1)
				{
					if (L == 0 && R == 0)
						mp[1][s] += cjh.second;
				}
				else
				{
					if (L == 0 && R == 0)
						mp[1][s ^ (1 << (j * 2 - 2)) ^ (2 << (j * 2))] += cjh.second;
					if (L == 1 && R == 2)
						if (i == nn && j == mm && s == 0)
							ans += cjh.second;
					if (L == 2 && R == 1)
						mp[1][s] += cjh.second;
					if (L == 1 && R == 1)
					{
						int cnt = 0;
						for (int pos = j; ; pos++)
						{
							if (((src >> (pos * 2)) & 3) == 1)
								cnt++;
							else if (((src >> (pos * 2)) & 3) == 2)
								cnt--;
							if (cnt == 0)
							{
								mp[1][s ^ (2 << (pos * 2)) ^ (1 << (pos * 2))] += cjh.second;
								break;
							}
						}
					}
					if (L == 2 && R == 2)
					{
						int cnt = 0;
						for (int pos = j - 1; ; pos--)
						{
							if (((src >> (pos * 2)) & 3) == 2)
								cnt++;
							else if (((src >> (pos * 2)) & 3) == 1)
								cnt--;
							if (cnt == 0)
							{
								mp[1][s ^ (2 << (pos * 2)) ^ (1 << (pos * 2))] += cjh.second;
								break;
							}
						}
					}
					if ((L == 0 && R != 0) || (L != 0 && R == 0))
					{
						mp[1][s ^ ((L + R) << (j * 2 - 2))] += cjh.second;
						mp[1][s ^ ((L + R) << (j * 2))] += cjh.second;
					}
				}
			}
			mp[0] = mp[1];
		}
		mp[1].clear();
		for (pair<const int, long long> &cjh : mp[0])
			if ((cjh.first & tot) == cjh.first)
				mp[1][(cjh.first & tot) << 2] += cjh.second;
		mp[0] = mp[1];
	}
	printf("%lld\n", ans);
	return 0;
}

还有一道例题[SCOI2011]地板，先鸽了，过段时间再发