2019 OO第一单元总结(表达式求导)

一. 基于度量的程序结构分析

1. 第一次作业

　　这次作业是我上手的第一个java程序，使用了4个类来实现功能。多项式采用两个arraylist来存，系数和幂指数一一对应。

 private ArrayList<BigInteger> coefs;
 private ArrayList<BigInteger> degrees;

　　四个类分别为

• Poly类，代表表达式；
• PolyDiff类，代表求导运算；
• PolyParse类，封装了格式检查，encoding（输入的多项式转为内部存储形式），优化，decoing（内部存储形式转为输出的多项式）方法；
• PolyDiffTest类，入口类

　　整个程序既有面向对象的味道(封装)，但不那么纯，也有面向过程的写法。

类图如下：

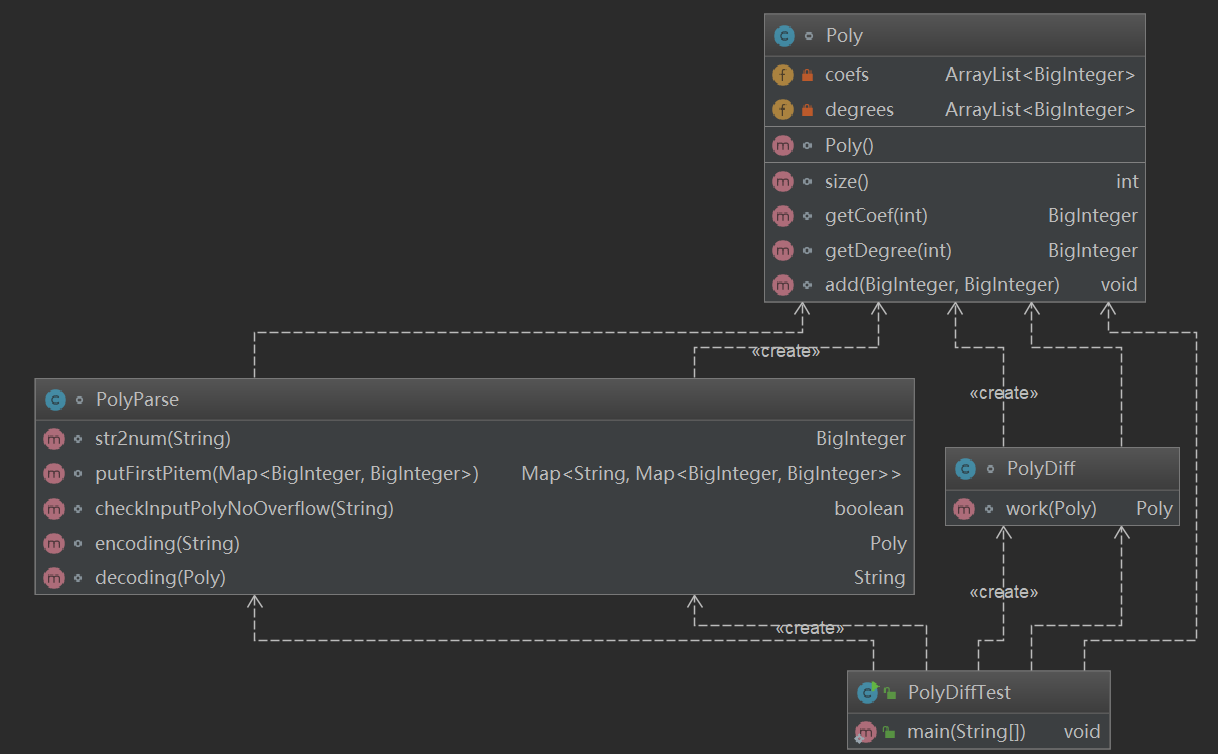
类复杂度分析如下：

       

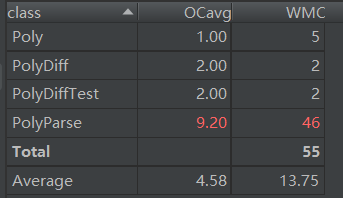
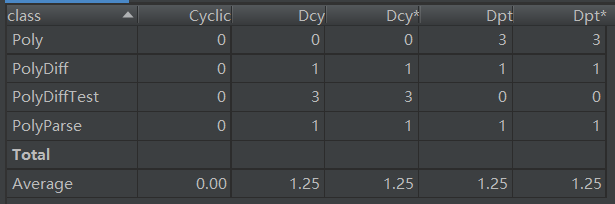
优缺点分析：　　

　　这里PolyParse类的代码尤其多，在整个设计中，PolyParse类是主类，完成了大多数功能，其他类是辅助类。这样的写法犯了面向对象的一个大忌：类失衡。究其原因，还是受到了面向过程思想的影响。其次可以直接用Hashmap而不是arraylist来存表达式。

　　对于第二次作业而言，本次作业的扩展性还行，给出了整个求导的框架。

---

2. 第二次作业

　　本次作业最重要的变化是加入了三角函数。为了使用上次作业的架构，我只改变了表达式的存储形式。对于求导，采用的方式还是和上次作业一样，直接带公式。关键是项的表示形式。

　　以 x, sin(x), cos(x) 做为基函数，对于任何项 kx^asin(x)^bcos(x)^c 都可以表示为 (k,(a,b,c))(k,(a,b,c)),

　　采用复合函数求导公式 (uvw)' = (uvw)′=u′vw+uv′w+uvw′ 得到的结果为3个项，具体形式可以拿公式直接得出来。

类图如下：

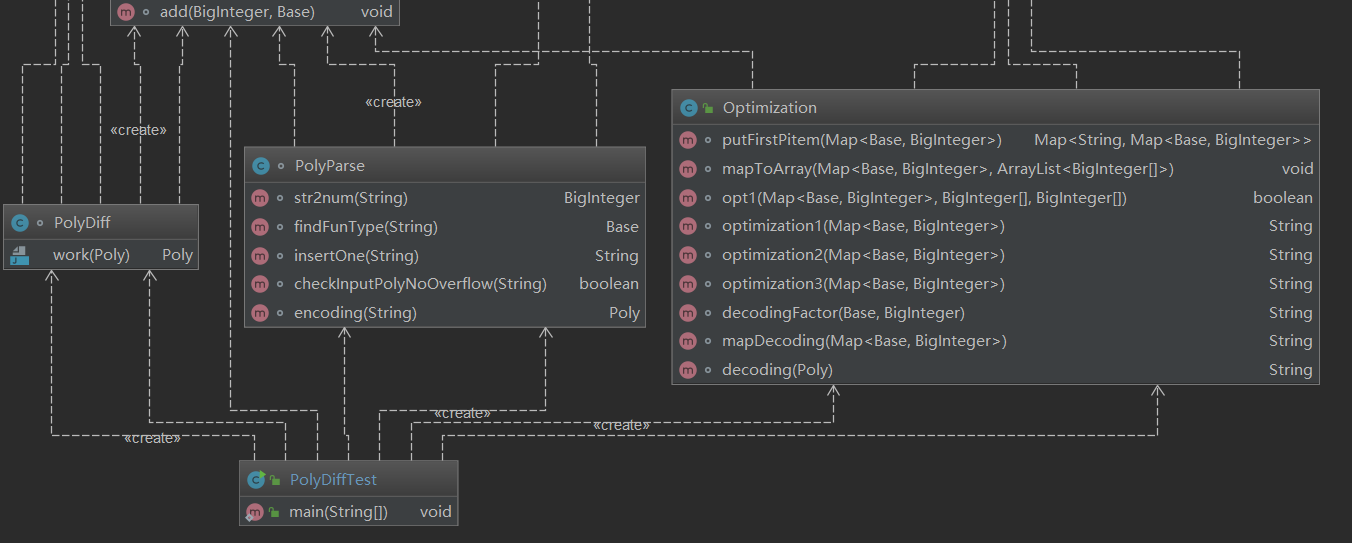
类复杂度分析如下：

    

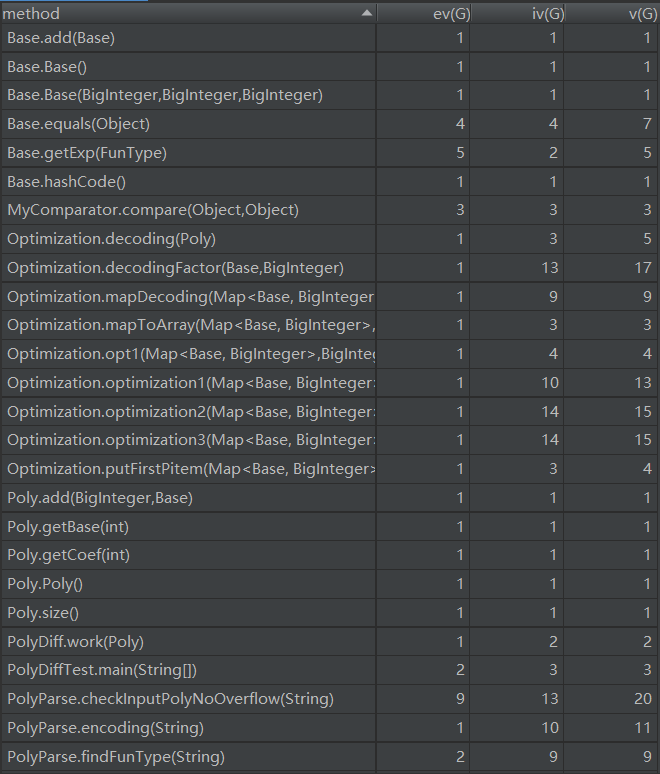
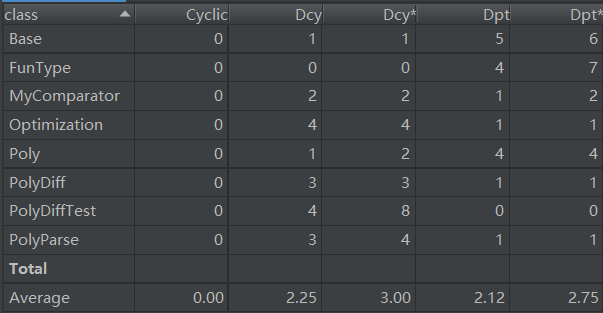
优缺点分析：　　

　　这里优化的类里面的代码尤其多，为了保证每个方法的行数小于限制行数，只能强行将优化函数拆成3个不同功能的优化，但里面有很多冗余的代码。

　　对于第三次作业而言，本次作业不具任何的扩展性，这种求导的框架走到了尽头。

---

3. 第三次作业

　　本次作业加入了嵌套因子和表达式因子，由于前两次作业不能扩展以及之前写过编译器的经验，这一次我是推倒重来，从头开始写了小型编译器。

　　求导过程可看作是一个翻译过程：源语言：原表达式，目标语言：求导后的表达式。指导书上对于item的要求看起来复杂，但拆成一个个小单元后，很容易就能写出item的文法，之后采用递归下降分析法，一次扫描，同时完成了格式检查和求导的工作。

　　我d得这次作业最精彩的是我的求导都是形式求导，实质是字符串的拼接。

　　比如a=b*c 有了b和c本身以及b和c求导后的表达式b',c'的string形式，套公式(字符串拼接)就可以得到c'=b'c+bc'的string形式。整个过程非常简单。不论是乘法，加法还是嵌套，都可以用这种方式解决。

类图如下：

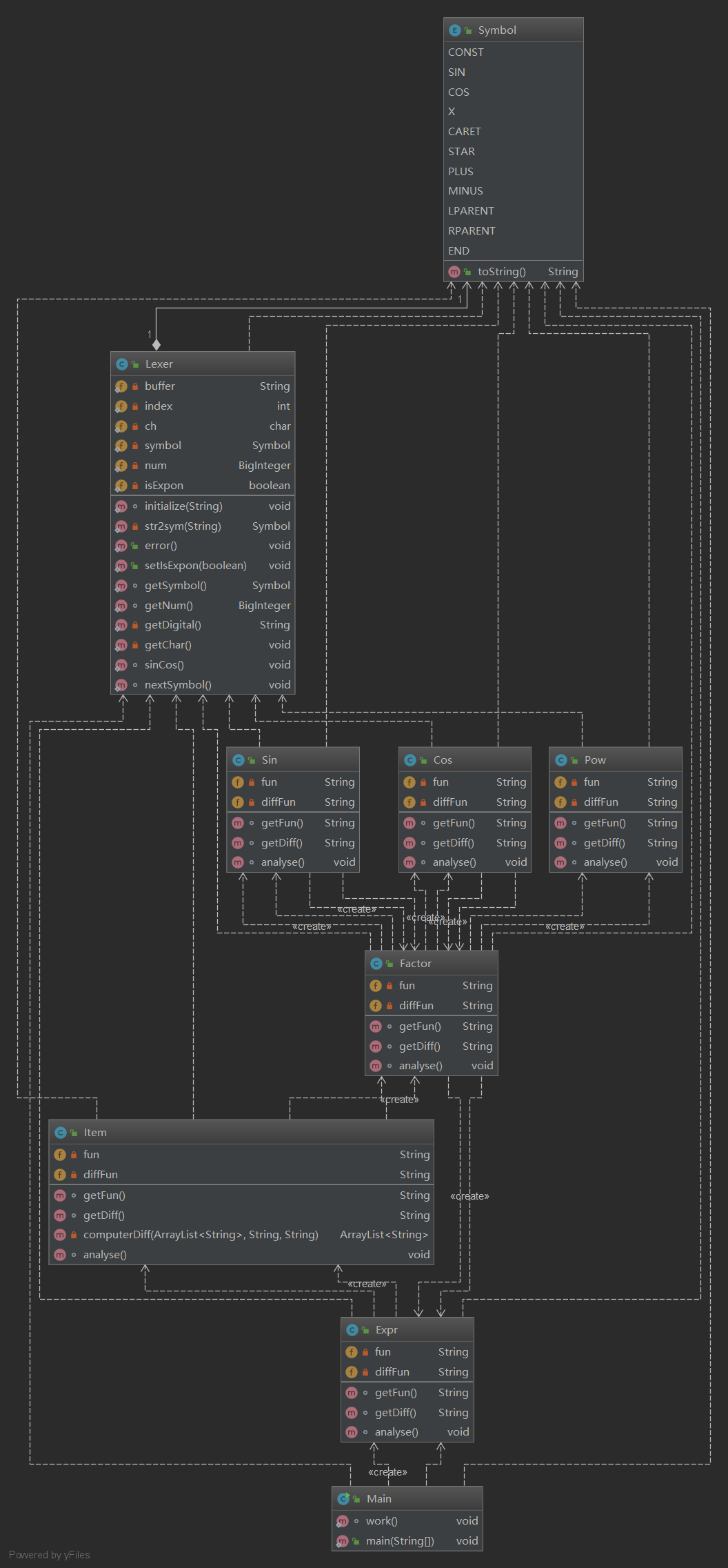
类复杂度分析如下：

          

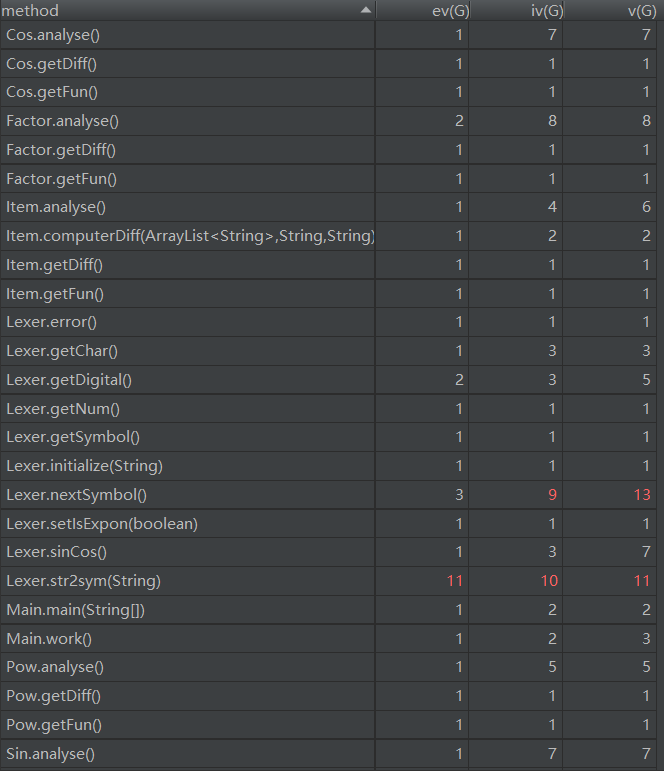
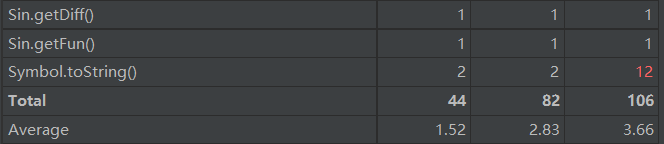
优缺点分析：

　　采用了编译器的经典架构：Expr,Item,Factor,Lexer,Symbol,Pow,Sin,Cos类的划分明确，职责清晰。类复杂度分析图中标红的地方是由于使用了大量的if,else或者switch，但这个也必须用，不知道有没有更好的对于if,else的改写方法。

　　还是只用了封装，继承，多态，接口一个都没用上。注意之后的重构部分会给出一些修改方法。

---

二. bug分析

第一次作业：　

　　较为简单，暂无bug发现

第二次作业：

　　这次作业的bug出在了优化部分，可谓是画蛇添足。

　　测试用例：3*x + sin(x)^5*cos(x) - sin (x)^3*cos(x) - sin(x)*cos(x)^5 + sin(x)*cos(x)^3

　　错误输出：7*sin(x)^2*cos(x)^2-4+7*cos(x)^2　　

　　特征：向map中添加元素的时候，没有先调用get()来得到原来的key之后再累加上去，而是直接调用put()方法覆盖了原来的key。导致程序中如果有一个以上sinx^2+cosx^2=1或1-sinx^2=cosx^2或1-cosx^2=sinx^2的合并时出现错误。

　　问题所在的类和方法：Optimization类的opt1，optimization1，optimization2方法。

　　bug位置与设计结构之间的相关性：优化类的结构一开始每个方法写的很长，超出了最大行数的限制，之后强行拆成了几个方法，导致方法的功能有些混乱，在测试时没有找到bug。

　　分类树角度分析程序在设计上的问题：分类树是一种使用树状结构来构造测试用例的方法，避免了测试用例的冗余。我在本次作业中构建的测试用例只针对了正确性，对于能够优化的用例，我只构造了几个，没有完全覆盖优化的函数。

第三次作业：

　　暂无bug发现，为了防止错误出现，没有做过多优化。

---

三. 测试方法

　　虽然我们没有互测，但自动测试可以显著提高测试效率，很有必要实现对拍程序。

1. 构建测试用例

　　对于第三次作业，情况较为复杂，采用随机生成大量用例的方法易生成大量类似测试用例，不能保证全覆盖。我依照指导书精心设计了30多个用例，保证了测试的全覆盖。

2. 测试方法

　　稍微修改java程序的Main方法，使其从文件读表达式，将结果输出到文件。使用python的sympy库编写对拍程序，符号求导，代入随机数运算后比对，实现了正确格式用例的测试。对于Wrong Format的测试，直接看java程序是否输出WF。

---

四. Applying Creational Pattern

　　第三次作业依旧没有使用继承和接口，但每个类的形式都是一样的。

 private String fun = "";
 private String diffFun = "";

 String getFun() {
     return fun;
 }

 String getDiff() {
     return diffFun;
 }

 void analyse() {
     ......
 }

　　重构：

　　新建一个父类对象Expression包含fun和diffFun变量成员，getFun()和getDiff()函数成员。由于每个子类的analyse()行为不一样，无法使用父类的getFun()和getDiff()完成功能，因此直接将analyse定义为一个接口。每一个子类需要继承父类Expression并且实现接口analyse。

　　我的设计思路中也体现出Factory Pattern的思想。因为语法分析的结果实质是构建了一个语法树，每一个父节点都会创建两个子节点，并且调用子节点的getFun()和getDiff()函数，整个过程是一个递归过程，最终从树的根节点上拿到结果。