POJ 2155 Matrix (矩形)

date：公元2017年7月19日适逢周三；

location：清北集训 杭州

point：二维树状数组/二维差分

Matrix

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 28325		Accepted: 10341

Description

Given an N*N matrix A, whose elements are either 0 or 1. A[i, j] means the number in the i-th row and j-th column. Initially we have A[i, j] = 0 (1 <= i, j <= N). 

We can change the matrix in the following way. Given a rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2), we change all the elements in the rectangle by using "not" operation (if it is a '0' then change it into '1' otherwise change it into '0'). To maintain the information of the matrix, you are asked to write a program to receive and execute two kinds of instructions. 

1. C x1 y1 x2 y2 (1 <= x1 <= x2 <= n, 1 <= y1 <= y2 <= n) changes the matrix by using the rectangle whose upper-left corner is (x1, y1) and lower-right corner is (x2, y2). 
2. Q x y (1 <= x, y <= n) querys A[x, y]. 

Input

The first line of the input is an integer X (X <= 10) representing the number of test cases. The following X blocks each represents a test case. 

The first line of each block contains two numbers N and T (2 <= N <= 1000, 1 <= T <= 50000) representing the size of the matrix and the number of the instructions. The following T lines each represents an instruction having the format "Q x y" or "C x1 y1 x2 y2", which has been described above. 

Output

For each querying output one line, which has an integer representing A[x, y]. 

There is a blank line between every two continuous test cases. 

Sample Input

1
2 10
C 2 1 2 2
Q 2 2
C 2 1 2 1
Q 1 1
C 1 1 2 1
C 1 2 1 2
C 1 1 2 2
Q 1 1
C 1 1 2 1
Q 2 1

Sample Output

1
0
0
1

Source

POJ Monthly,Lou Tiancheng

 

 

题目翻译（有道滋滋）

给一个N * N矩阵,其元素是0或1。(i,j)意味着i行和j列数。一开始我们有一个(i,j)= 0(1 < = i,j < = N)。

我们可以改变矩阵以以下方式。给定一个矩形的左上角(x1,y1),右下角(x2,y2),我们改变矩形中的所有元素用“不”操作(如果它是一个' 0 '然后改变它为' 1 '否则改变成“0”)。保持矩阵的信息,你被要求写一个程序接收和执行两种指令。

1。C(x1,y1 x2 y2 x1 < = x2(1 < = < = n,1 < = y1 < = y2 < = n)变化矩阵,利用矩形的左上角(x1,y1),右下角(x2,y2)。
2。Q x y(1 < = x,y < = n)查询(x,y)。

输入

输入的第一行是一个整数X(X < = 10)代表测试用例的数量。以下X块每个表示一个测试用例。

每一块的第一行包含两个数N和T(2 < = N < = 1000,1 < = T < = 50000)代表矩阵的大小和数量的指示。以下T行每个代表一个指令的格式“Q x y”或“C x1 y1 x2 y2”,上面所描述的。

输出

为每个查询输出一行,一个整数代表一个(x,y)。

之间有一个空行每两个连续的测试用例。

样例输入

1
2 10
C 2 1 2 2
Q 2 2
C 2 1 2 1
Q 1 1
C 1 1 2 1
C 1 2 1 2
C 1 1 2 2
Q 1 1
C 1 1 2 1
Q 2 1

样例输出

1
0
0
1

题解：据说本题是用数学方法来做，但是oycy大学霸+lsh大学霸好像在我写这篇题解之前已经研究了2个小时了……
再说那天的数学听得我对数学没有信心了，所以压根就没想到数学；
不是说数学不可以，但是太过困难了（深切感受），
一想到数学便睡意袭来，
然后大概花了40分钟便想出一个基于二维树状数组的思路：
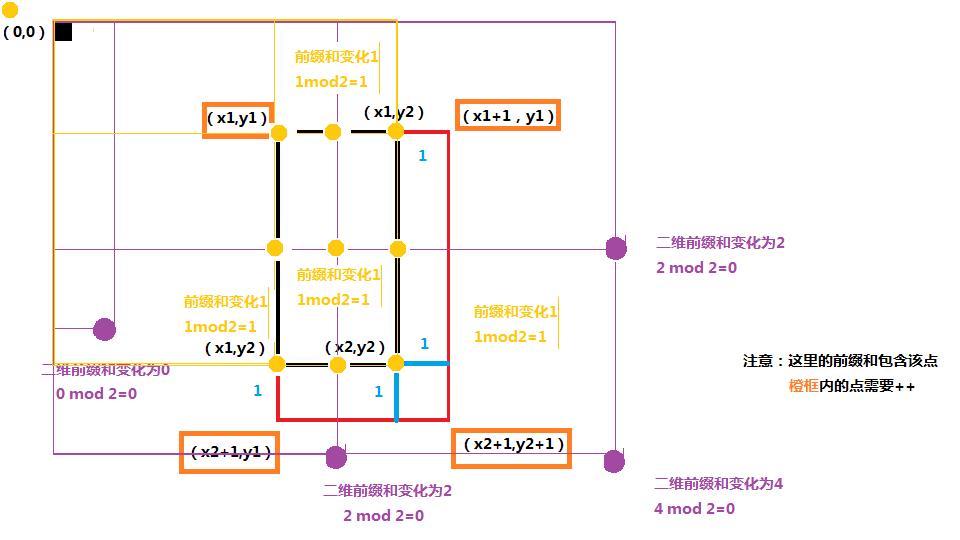
现在我们设需要not变换的子矩阵左上坐标为(x1,y1)右下坐标(x2,y2)
不妨拓展1格，方便我们解题，先看到一幅图（拓展后）
注意到左上方有一个小黄人（这没什么用，请自行过滤）
黑方框为(0,0)

黑方框代表我们需要not的区域 红方框代表拓展出来的区域
TIPS:红方框边界上的点没画（lazy++），自己推吧，懒得画了，符合的。
在我的解题方案中，我们只要将点（橙框的4点）++
a[x1,y1]++
a[x2+1,y1]++
a[x1+1,y1]++
a[x2+1,y2+1]++
可以证明在黑方框外的任一点的二维前缀和的增量r mod 2 恒等于 0
而黑方框内的任一点的二维前缀和的增量r mod 2 恒等于 1
当然这是对于第一下C，当然基于第2~q次，同理，我们可以通过增量r mod 2=0 or 1，来判断该点到底是 1 还是 0
需要注意的，我们来简化问题，就是因为初始值为0所以我们不需要求坐标增量r只需要求出前缀和w即可
二维前缀和的最快维护方案是二维树状数组；具体维护不在多讲（本质是为树状数组+循环）
这样我们只要使4个点的权值++，维护前缀和，求Q(x,y)只要C(x,y)mod 2=1 则最终的点(x,y)就是1，反之就是0
做完了~~

用not 来维护树状数组你就中陷阱了；
或者用dp来做，也是行不通的；

希望lsh+oycy大学霸orz能够早日用数学AC本题！

就是该算法的时间复杂度的分析在程序后，请自行查看。

代码:

uses math;
var n,m,i,j,t,x1,x2,y1,y2,q,x,y,tt,ii:longint;
    c:array[..,..]of longint;
    ch:char;
function lowbit(x:longint):longint;
begin
 exit(x and (-x));
end;
procedure update(xx,yy,opx:longint);//二维树状数组把数组中a[xx]+yy并且跟新树状数组c[]
var ty,x,y:longint;
begin
 x:=xx; y:=yy;
 ty:=yy;
  while x<=n do begin
   y:=ty;
   while y<=n do begin
    c[x,y]:=c[x,y]+opx;
    y:=y+lowbit(y);
   end;
   x:=x+lowbit(x);
  end;
end;
function query(x,y:longint):longint;//询问a二维矩阵a[]前缀和
var  sum,ty:longint;
begin
 sum:=;
 ty:=y;
 while x> do begin
  y:=ty;
  while y> do begin
   sum:=sum+c[x,y];
   y:=y-lowbit(y);
  end;
  x:=x-lowbit(x);
 end;
 exit(sum);
end;
begin
readln(tt);//tt组数据
for ii:= to tt do begin
 readln(n,q);//n*n矩阵，q个操作
 for i:= to q do begin
  read(ch);//ch为指示符
  case ch of
   'C':begin readln(x1,y1,x2,y2);
      update(x1,y1,);   update(x1,y2+,);
      update(x2+,y1,); update(x2+,y2+,);//4个橙色的点依次更改
   end;
   'Q':begin readln(x,y); writeln(query(x,y) mod );end;//判断mod 2？=1
  end;
 end;
 writeln;
 end;
end.

我们来计算时间复杂度：

对于1次程序tt++前完成，q个询问，

如果是Q则复杂度是O(log n) 如果是C则复杂度为O(4 log n)，最坏时间复杂度为O(4 log n)

那么对于1次完整的解决，我们最坏的时间复杂度为O (4q log n)

对于完整的tt次解决，最坏的时间复杂度是O(4*q*tt*log n)

2 <= N <= 1000, 1 <= q<= 50000; tt<=10;

那么最坏情况的常数为O(4*50000*10*10)=O(2000w)

没有超时，完美解决！

希望lsh+oycy大学霸orz能够早日用数学AC本题！