JAVA常见算法题(三十三)---求子串在字符串中出现的次数

计算某字符串中子串出现的次数。

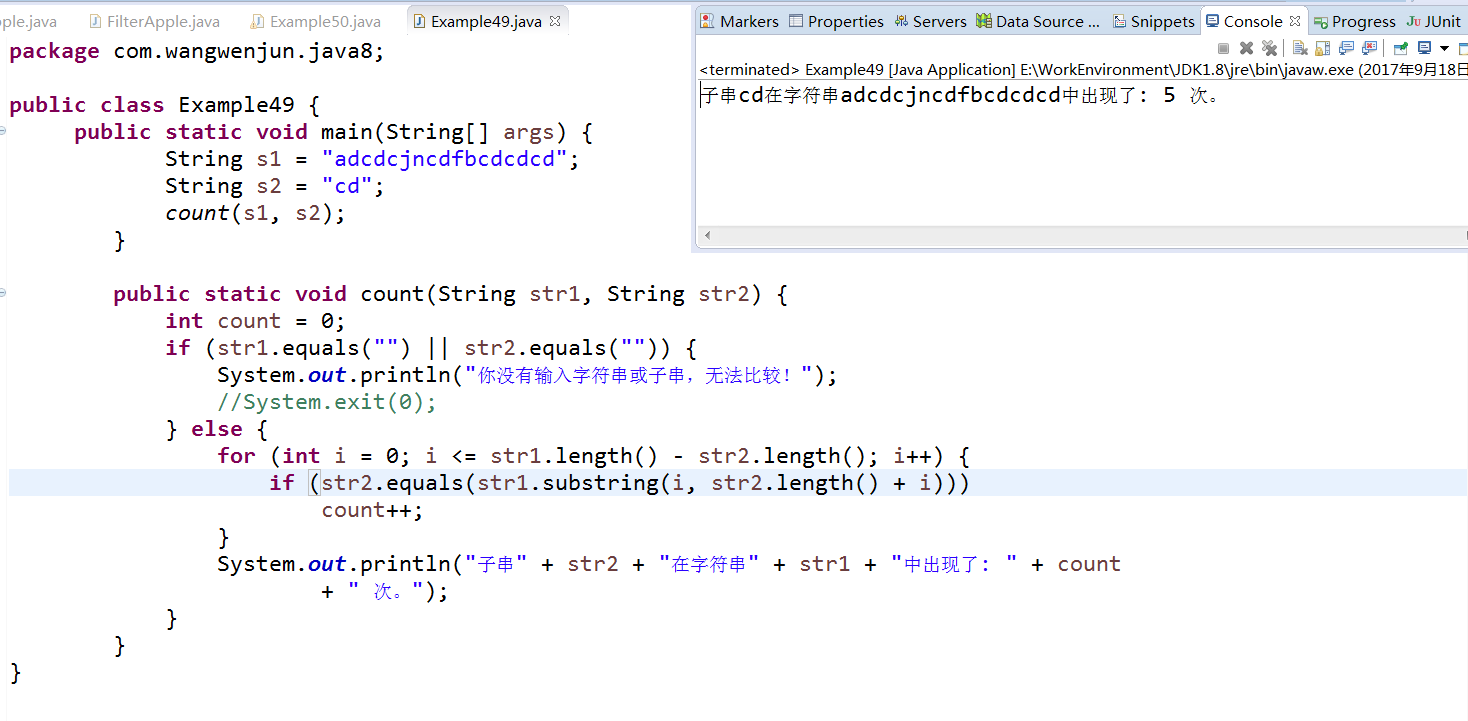
public static void main(String[] args) {
            String s1 = "adcdcjncdfbcdcdcd";
            String s2 = "cd";
            count(s1, s2);
        }
 
        public static void count(String str1, String str2) {
            int count = 0;
            if (str1.equals("") || str2.equals("")) {
                System.out.println("你没有输入字符串或子串，无法比较！");
                //System.exit(0);
            } else {
                for (int i = 0; i <= str1.length() - str2.length(); i++) {
                    if (str2.equals(str1.substring(i, str2.length() + i)))
                        count++;
                }
                System.out.println("子串" + str2 + "在字符串" + str1 + "中出现了: " + count
                        + " 次。");
            }
        }