SPOJ TWOPATHS Two Paths

　　题目意思：给一棵树，找到俩个不相交的通路，使得这俩个通路的长度和乘机最大；

解法：

　　小哥一看呵呵 这不就是枚举点 然后求俩边的树的直径在相乘求个最大值的题么！

　　呵呵 这个N 有100000 当时就不玩了；

　　学长指导了下我；

　　俺会了！/灯泡

　　在枚举点在书的直径上时点的左右的最长的链无非这几种情况如图（红色是树得直径）（蓝色和绿色是俩种情况）

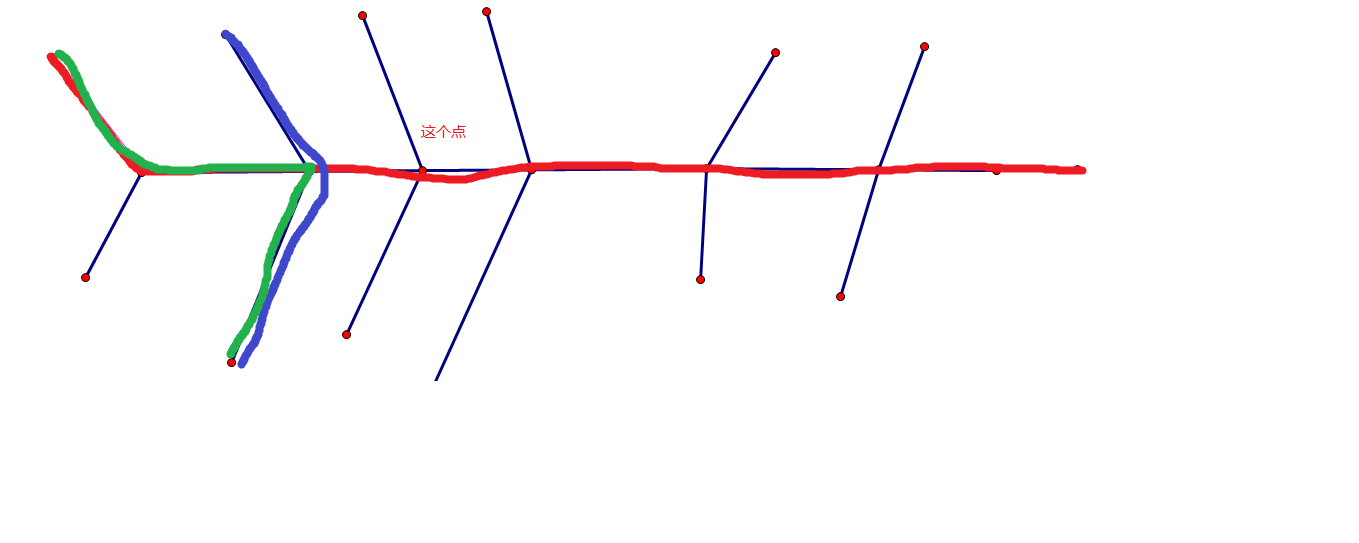
　　无非就 蓝色和绿色这个俩种，所以这个答案和直径有很大的关系！

不在直径上时：一边肯定是直径了另一半呢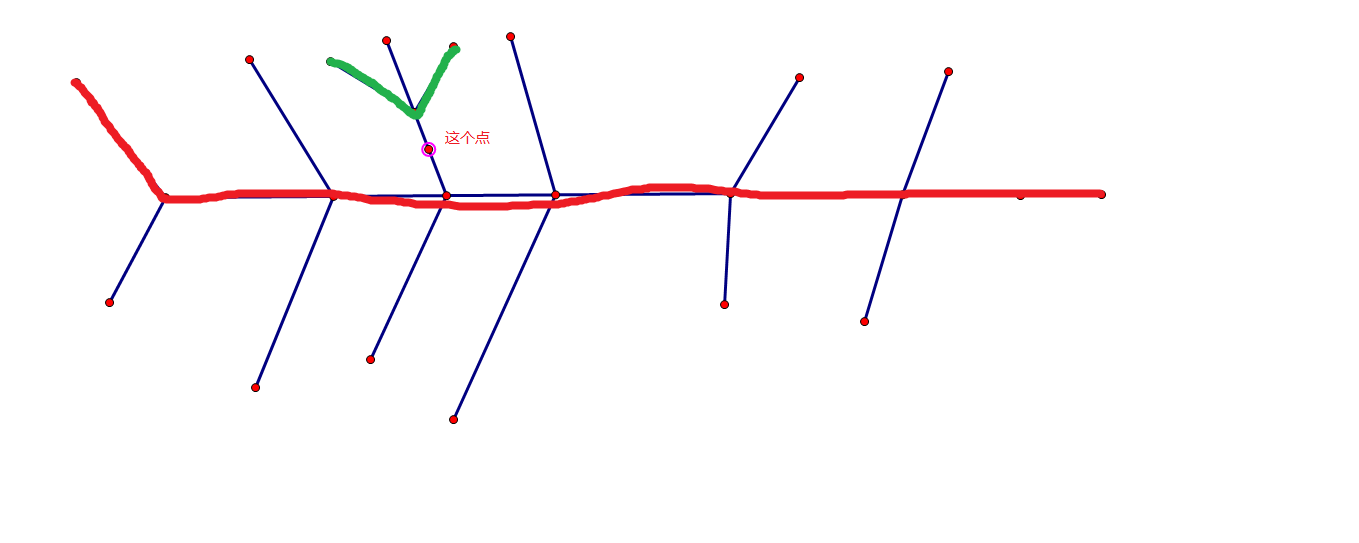？如图；

　　解的过程：

　　　　1: 想求出直径的点顺序的 存在一个数组内；

　　　　2: 求出和每个直径上节点相邻的  最大和次大 和直径不相连的  链的 长度  并求出Max（这个链的点都不在直径上）

　　　　3：O（n）枚举点并求出这个点的左右的长度最值

　　　　4：由3的结果求出最大的ANS ，在和树得直径*Max取最值

　　over：

代码

#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int INF=0x7fffffff;
const int maxn=;
struct Edge
{
    int to,pre;
    Edge (int to=,int pre=):to(to),pre(pre){}
};
Edge edge[maxn*];
int head[maxn],pos;
bool vis[maxn];
bool in_line[maxn];
int ko[maxn],pos_ko;
int dp[maxn][];
int dp1[maxn],dp2[maxn];
struct info
{
    int p,pre;
};
info  que[maxn];
void inint()
{
    memset(head,-,sizeof(head));
    pos=pos_ko=;
    memset(dp,,sizeof(dp));
    memset(in_line,false,sizeof(in_line));
    memset(dp1,,sizeof(dp1));
    memset(dp2,,sizeof(dp2));
}
void add_edge(int s,int to)
{
    edge[pos]=Edge(to,head[s]);
    head[s]=pos++;
}
void make(int P)
{
    if(que[P].pre!=-)make(que[P].pre);
    ko[pos_ko++]=que[P].p;
    in_line[que[P].p]=true;
}
int bfs(int t,bool flag)
{
    memset(vis,false,sizeof(vis));
    int h=,r=;
    que[].p=t;
    que[].pre=-;
    vis[t]=true;
    int x;
    while(h<r)
    {
        x=que[h++].p;
        for(int i=head[x];~i;i=edge[i].pre)
        {
            Edge &tmp=edge[i];
            if(!vis[tmp.to])
                que[r].p=tmp.to,
                que[r++].pre=h-,
                vis[tmp.to]=true;
        }
    }
    if(flag)make(r-);
    return que[r-].p;
}
void get_it(int key,int t)
{
    if(key>dp[t][])dp[t][]=dp[t][],
                    dp[t][]=key;
    else if(key>dp[t][])
                    dp[t][]=key;
}
int Max;
int dfs(int pa,int &s,int &t)
{
    int key,ans=;
    for(int w=head[s];~w;w=edge[w].pre)
    {
        Edge &tmp=edge[w];
        if(tmp.to==pa||in_line[tmp.to])continue;
        key=dfs(s,tmp.to,t);
        if(pa==-) get_it(key,t);
        if(pa!=-)
        {
            if(ans)
                Max=max(Max,ans-+key);
            else
                Max=max(Max,key);
        }
        ans=max(ans,key+);
    }
    if(pa==-)Max=max(Max,ans-);
    return ans==?:ans;
}
void solve(int &n)
{

    long long  ans=;
    Max=;
    int p1=bfs(,false),p2=bfs(p1,true);
    int Max1;
    for(int i=;i<pos_ko;i++)
        dfs(-,ko[i],i);
    ans=(pos_ko-)*Max;
    --pos_ko;
    for(int i=;i<pos_ko;i++)
    {
        dp1[i]=max(dp1[i-],i+dp[i][]);
        dp1[i]=max(dp1[i],dp[i][]+dp[i][]);
    }
    for(int i=pos_ko-;i>=;i--)
    {
        dp2[i]=max(dp2[i+],pos_ko-i+dp[i][]);
        dp2[i]=max(dp2[i],dp[i][]+dp[i][]);
    }
    for(int i=;i<pos_ko;i++)
        ans=max(ans,(long long)dp1[i]*dp2[i+]);
    ans=max(ans,(long long ));
    printf("%lld\n",ans);
}
int main()
{
    int n;
    int a,b;
    while(~scanf("%d",&n))
    {
        inint();
        for(int i=;i<=n;i++)
        {
            scanf("%d%d",&a,&b);
            add_edge(a,b);
            add_edge(b,a);
        }
        solve(n);
    }
    return ;
}