python 回溯法 子集树模板 系列 —— 2、迷宫问题

问题

给定一个迷宫，入口已知。问是否有路径从入口到出口，若有则输出一条这样的路径。注意移动可以从上、下、左、右、上左、上右、下左、下右八个方向进行。迷宫输入0表示可走，输入1表示墙。为方便起见，用1将迷宫围起来避免边界问题。

分析

考虑到左、右是相对的，因此修改为：北、东北、东、东南、南、西南、西、西北八个方向。在任意一格内，有8个方向可以选择，亦即8种状态可选。因此从入口格子开始，每进入一格都要遍历这8种状态。

显然，可以套用回溯法的子集树模板。

注意，解的长度是不固定的。

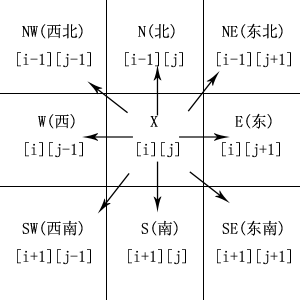
图片来源：点我

代码

# 迷宫（1是墙，0是通路）
maze = [[1,1,1,1,1,1,1,1,1,1],
        [0,0,1,0,1,1,1,1,0,1],
        [1,1,0,1,0,1,1,0,1,1],
        [1,0,1,1,1,0,0,1,1,1],
        [1,1,1,0,0,1,1,0,1,1],
        [1,1,0,1,1,1,1,1,0,1],
        [1,0,1,0,0,1,1,1,1,0],
        [1,1,1,1,1,0,1,1,1,1]]

m, n = 8, 10   # 8行，10列
entry = (1,0)  # 迷宫入口
path = [entry] # 一个解（路径）
paths = []     # 一组解

# 移动的方向（顺时针8个：N, EN, E, ES, S, WS, W, WN）
directions = [(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1),(-1,-1)]

# 冲突检测
def conflict(nx, ny):
    global m,n,maze

    # 是否在迷宫中，以及是否可通行
    if 0 <= nx < m and 0 <= ny < n and maze[nx][ny]==0:
        return False

    return True

# 套用子集树模板
def walk(x, y): # 到达(x,y)格子
    global entry,m,n,maze,path,paths,directions

    if (x,y) != entry and (x % (m-1) ==0 or y % (n-1) == 0):  # 出口
        #print(path)
        paths.append(path[:]) # 直接保存，未做最优化
    else:
        for d in directions: # 遍历8个方向(亦即8个状态)
            nx, ny = x+d[0], y+d[1]
            path.append((nx,ny))     # 保存，新坐标入栈
            if not conflict(nx, ny): # 剪枝
                maze[nx][ny] = 2         # 标记，已访问（奇怪，此两句只能放在if区块内！）
                walk(nx, ny)
                maze[nx][ny] = 0         # 回溯，恢复
            path.pop()               # 回溯，出栈

# 解的可视化（根据一个解x，复原迷宫路径，'2'表示通路）
def show(path):
    global maze

    import pprint, copy

    maze2 = copy.deepcopy(maze)

    for p in path:
        maze2[p[0]][p[1]] = 2 # 通路

    pprint.pprint(maze)  # 原迷宫
    print()
    pprint.pprint(maze2) # 带通路的迷宫

# 测试
walk(1,0)
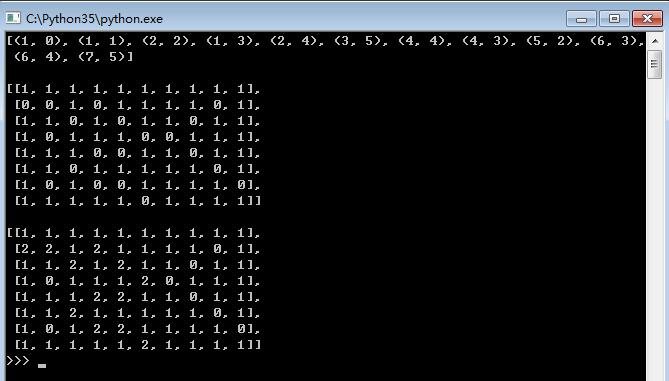
print(paths[-1], '\n') # 看看最后一条路径
show(paths[-1])

效果图