无监督学习——K-均值聚类算法对未标注数据分组

无监督学习

和监督学习不同的是，在无监督学习中数据并没有标签（分类）。无监督学习需要通过算法找到这些数据内在的规律，将他们分类。（如下图中的数据，并没有标签，大概可以看出数据集可以分为三类，它就是一个无监督学习过程。）

无监督学习没有训练过程。

---

聚类算法

该算法将相似的对象轨道同一个簇中，有点像全自动分类。簇内的对象越相似它的分类效果越好。

未接触这个概念可能觉得很高大上，稍微看了一会其实算法的思路和KNN一样很简单。

原始数据集如下（数据有两个特征，分别用横纵坐标表示），原始数据集并没有任何标签和分类信息：

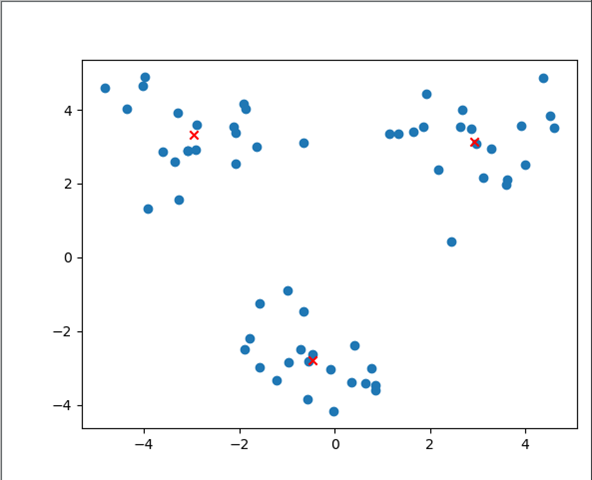
由图中的数据可以大概判断，该数据集可以分为三类数据（定义为0,1,2），那么每个点到底属于哪个分类呢，这里通过K-均值聚类算法得到三个质心点，并根据每个点到三个质心的距离进行分类（到0,1,2三个质心距离最近，则将该数据分为该类），计算出的三个质心点如下图（图中红叉点表示）：

---

K-均值聚类算法

该算法的流程如下：

1. 加载数据集
2. 数据初始化
     2.1 创建随机质心点
     2.2 穿件保存结果的各个矩阵/数组
3. 多次迭代 （判断所有点的分类是否发生变化）
     3.1 计算所有点的分类
     3.2 根据3.1分类结果，重新计算质心点（用属于当前类的数据取平均作为新的质心点）
4. 返回数据

该算法缺点：

算法容易收敛到局部最小值，而非全局最小值。（局部最小值指结果还可以，但是并非最好结果，全局最小值时可能的最好结果）

---

二分K-均值聚类算法

SSE： 度量聚类效果的指标（Sum of Squared Erro，误差平方和）

SSE越小说明所有数据点越接近他们的质心，聚类效果也就越好。

该算法的流程如下：

1. 将所有点看成一个簇
2. 当簇数目小于K时
      2.1 对每个簇
         2.1.1 计算总误差
         2.1.2 在给定簇上面进行K-均值聚类（K=2）
         2.1.2 计算在该簇上一分为二之后的总误差
      2.2 选择是的误差最小的那个簇进行划分

---

Python实现

数据加载

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat

数据的形式如下，和监督学习数据形式最大的区别是这里的数据是不带有标签的数据。每个数据是一个二维的向量。

3.275154    2.957587
-3.344465    2.603513
0.355083    -3.376585
1.852435    3.547351
-2.078973    2.552013
-0.993756    -0.884433
2.682252    4.007573
-3.087776    2.878713
-1.565978    -1.256985
2.441611    0.444826
-0.659487    3.111284
-0.459601    -2.618005
2.177680    2.387793
-2.920969    2.917485
-0.028814    -4.168078
3.625746    2.119041
-3.912363    1.325108
-0.551694    -2.814223
2.855808    3.483301
..................

 

向量欧式距离计算函数

def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

 

随机产生n个质心

def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:,j])
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids

 

K-均值聚类算法

        缺点： 该算法必须要业务提前输入分类的个数K。

该函数返回值为质心坐标centroids，以及每个点最近的质心（即该点的分类结果）和它的距离clusterAssment。

这里需要注意迭代的终止条件： clusterChanged，该标记位用来标记此次迭代是否有数据的分类和上一次得带不同，如果当前这次迭代的对所有数据的分类和上一次分类结果完全相同，则不再继续迭代。

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    #计算数据个数
    m = shape(dataSet)[0]
    # 存放每个数据到哪个质心距离最近，以及它的距离值
    clusterAssment = mat(zeros((m,2)))#create mat to assign data points
                                      #to a centroid, also holds SE of each point
    centroids = createCent(dataSet, k)#产生随机的质心点（通过迭代，逐步变得精确）
    clusterChanged = True             #分类是否改变，迭代结束的条件
    while clusterChanged:
        clusterChanged = False
        for i in range(m):#for each data point assign it to the closest centroid
            minDist = inf; minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print centroids
        for cent in range(k):#recalculate centroids
                #ptsInClust表示到该质心距离最近的点集合
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster
            #将质心坐标 用最近点坐标的均值代替，所以称为均值聚类算法
            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean
    return centroids, clusterAssment

二分K-均值算法

该算法的输入和输出和K-均值算都相同，只是它的内部实现更复杂。

def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList =[centroid0] #create a list with one centroid
    for j in range(m):#calc initial Error
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
            print "sseSplit, and notSplit: ",sseSplit,sseNotSplit
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print 'the bestCentToSplit is: ',bestCentToSplit
        print 'the len of bestClustAss is: ', len(bestClustAss)
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE
    return mat(centList), clusterAssment

其它机器学习算法：

监督学习——随机梯度下降算法（sgd）和批梯度下降算法（bgd）

监督学习——决策树理论与实践（上）：分类决策树

监督学习——决策树理论与实践（下）：回归决策树（CART）

监督学习——K邻近算法及数字识别实践

监督学习——朴素贝叶斯分类理论与实践

监督学习——logistic进行二分类（python）

监督学习——AdaBoost元算法提高分类性能

参考：

《机器学习实战》