CS229 6.3 Neurons Networks Gradient Checking
BP算法很难调试,一般情况下会隐隐存在一些小问题,比如(off-by-one error),即只有部分层的权重得到训练,或者忘记计算bais unit,这虽然会得到一个正确的结果,但效果差于准确BP得到的结果。
有了cost function,目标是求出一组参数W,b,这里以 表示,cost function 暂且记做
表示,cost function 暂且记做 。假设
。假设 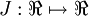 ,则
,则 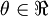 ,即一维情况下的Gradient Descent:
,即一维情况下的Gradient Descent:
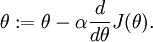
根据6.2中对单个参数单个样本的求导公式:
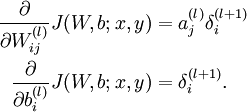
可以得到每个参数的偏导数,对所有样本累计求和,可以得到所有训练数据对参数  的偏导数记做
的偏导数记做 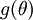 ,
,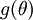 是靠BP算法求得的,为了验证其正确性,看下图回忆导数公式:
是靠BP算法求得的,为了验证其正确性,看下图回忆导数公式:
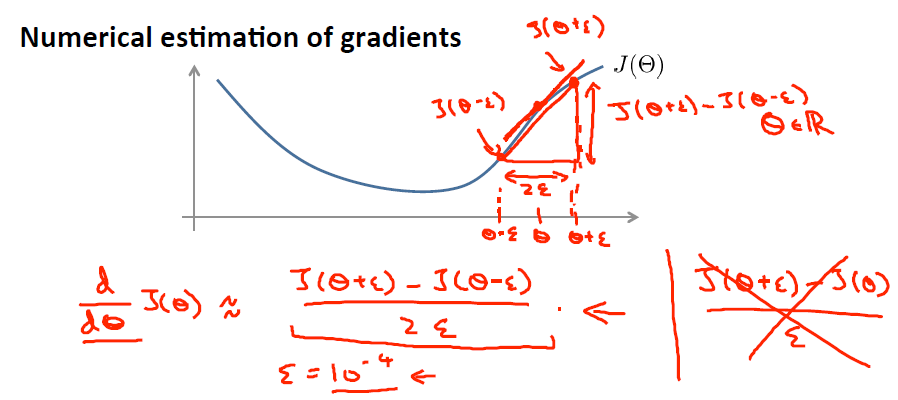
可见有: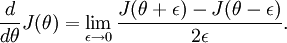 那么对于任意
那么对于任意  值,我们都可以对等式左边的导数用:
值,我们都可以对等式左边的导数用:
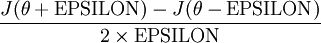 来近似。
来近似。
给定一个被认为能计算 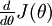 的函数
的函数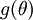 ,可以用下面的数值检验公式
,可以用下面的数值检验公式
应用时,通常把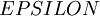 设置为一个很小的常量,比如在
设置为一个很小的常量,比如在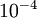 数量级,最好不要太小了,会造成数值的舍入误差。上式两端值的接近程度取决于
数量级,最好不要太小了,会造成数值的舍入误差。上式两端值的接近程度取决于 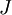 的具体形式。假定
的具体形式。假定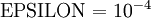 的情况下,上式左右两端至少有4位有效数字是一样的(通常会更多)。
的情况下,上式左右两端至少有4位有效数字是一样的(通常会更多)。
当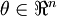 是一个n维向量而不是实数时,且
是一个n维向量而不是实数时,且 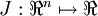 ,在 Neorons Network 中,J(W,b)可以想象为 W,b 组合扩展而成的一个长向量
,在 Neorons Network 中,J(W,b)可以想象为 W,b 组合扩展而成的一个长向量  ,现在又一个计算
,现在又一个计算 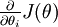 的函数
的函数 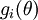 ,如何检验
,如何检验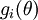 能否输出到正确结果呢,用
能否输出到正确结果呢,用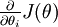 的取值来检验,对于向量的偏导数:
的取值来检验,对于向量的偏导数:

根据上图,对  i 求导时,只需要在向量的第i维上进行加减操作,然后求值即可,定义
i 求导时,只需要在向量的第i维上进行加减操作,然后求值即可,定义 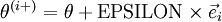 ,其中
,其中
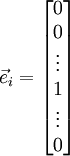
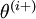 和
和  几乎相同,除了第
几乎相同,除了第  行元素增加了
行元素增加了 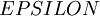 ,类似地,
,类似地,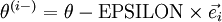 得到的第
得到的第  行减小了
行减小了 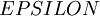 ,然后求导并与
,然后求导并与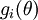 比较:
比较:
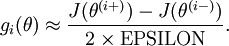
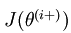 中的参数对应的是参数向量中一个分量的细微变化,损失函数J 在不同情况下会有不同的值(比如三层NN 或者 三层autoencoder(需加上稀疏项)),上式中左边为BP算法的结果,右边为真正的梯度,只要两者很接近,说明BP算法是在正确工作,对于梯度下降中的参数是按照如下方式进行更新的:
中的参数对应的是参数向量中一个分量的细微变化,损失函数J 在不同情况下会有不同的值(比如三层NN 或者 三层autoencoder(需加上稀疏项)),上式中左边为BP算法的结果,右边为真正的梯度,只要两者很接近,说明BP算法是在正确工作,对于梯度下降中的参数是按照如下方式进行更新的:
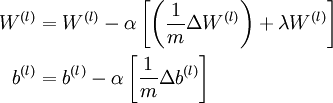
即有 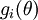 分别为:
分别为:
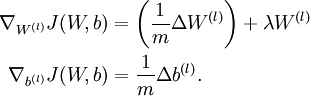
最后只需总体损失函数J(W,b)的偏导数与上述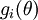 的值比较即可。
的值比较即可。
除了梯度下降外,其他的常见的优化算法:1) 自适应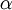 的步长,2) BFGS L-BFGS,3) SGD,4) 共轭梯度算法,以后涉及到再看。
的步长,2) BFGS L-BFGS,3) SGD,4) 共轭梯度算法,以后涉及到再看。
CS229 6.3 Neurons Networks Gradient Checking的更多相关文章
- (六) 6.3 Neurons Networks Gradient Checking
BP算法很难调试,一般情况下会隐隐存在一些小问题,比如(off-by-one error),即只有部分层的权重得到训练,或者忘记计算bais unit,这虽然会得到一个正确的结果,但效果差于准确BP得 ...
- CS229 6.10 Neurons Networks implements of softmax regression
softmax可以看做只有输入和输出的Neurons Networks,如下图: 其参数数量为k*(n+1) ,但在本实现中没有加入截距项,所以参数为k*n的矩阵. 对损失函数J(θ)的形式有: 算法 ...
- CS229 6.16 Neurons Networks linear decoders and its implements
Sparse AutoEncoder是一个三层结构的网络,分别为输入输出与隐层,前边自编码器的描述可知,神经网络中的神经元都采用相同的激励函数,Linear Decoders 修改了自编码器的定义,对 ...
- CS229 6.13 Neurons Networks Implements of stack autoencoder
对于加深网络层数带来的问题,(gradient diffuse 局部最优等)可以使用逐层预训练(pre-training)的方法来避免 Stack-Autoencoder是一种逐层贪婪(Greedy ...
- CS229 6.5 Neurons Networks Implements of Sparse Autoencoder
sparse autoencoder的一个实例练习,这个例子所要实现的内容大概如下:从给定的很多张自然图片中截取出大小为8*8的小patches图片共10000张,现在需要用sparse autoen ...
- CS229 6.1 Neurons Networks Representation
面对复杂的非线性可分的样本是,使用浅层分类器如Logistic等需要对样本进行复杂的映射,使得样本在映射后的空间是线性可分的,但在原始空间,分类边界可能是复杂的曲线.比如下图的样本只是在2维情形下的示 ...
- CS229 6.2 Neurons Networks Backpropagation Algorithm
今天得主题是BP算法.大规模的神经网络可以使用batch gradient descent算法求解,也可以使用 stochastic gradient descent 算法,求解的关键问题在于求得每层 ...
- CS229 6.15 Neurons Networks Deep Belief Networks
Hintion老爷子在06年的science上的论文里阐述了 RBMs 可以堆叠起来并且通过逐层贪婪的方式来训练,这种网络被称作Deep Belife Networks(DBN),DBN是一种可以学习 ...
- CS229 6.12 Neurons Networks from self-taught learning to deep network
self-taught learning 在特征提取方面完全是用的无监督的方法,对于有标记的数据,可以结合有监督学习来对上述方法得到的参数进行微调,从而得到一个更加准确的参数a. 在self-taug ...
随机推荐
- 利用 groupby apply list 分组合并字符
利用 groupby apply list 分组合并字符 因为需要对数据进行分组和合并字符,找到了以下方法. 有点类似 SQL 的 Group BY. import pandas as pd impo ...
- day40 css高级选择器
一.高级选择器 高级选择器分为:后代选择器.子代选择器.并集选择器.交集选择器 后代选择器 使用空格表示后代选择器.顾名思义,父元素的后代(包括儿子,孙子,重孙子) .container p{ col ...
- day4 大纲笔记
01 上周内容回顾 int bool str int <---> str: i1 = 100 str(i1) s1 = '10' int(s1) 字符串必须是数字组成. int <- ...
- 关于class produre
很好理解 type TMessageHandler = class //使得回车消息转换成Tab消息 class procedure AppMessage(var Msg:TMsg;var Handl ...
- 解决“chrome adobe flash player不是最新版本”的方法
chrome地址栏输入chrome://components 更新flash后,重启chrome即可,可能需要搭梯子才能更新.
- PHP批量添加数据
<?php // 连接数据库 header('content-type:text/html;charset=utf-8'); define('DB_HOST','127.0.0.1'); def ...
- 使用R语言-计算均值,方差等
R语言对于数值计算很方便,最近用到了计算方差,标准差的功能,特记录. 数据准备 height <- c(6.00, 5.92, 5.58, 5.92) 1 计算均值 mean(height) [ ...
- 第一个react
个人觉着react和vue是很相似的,之前还转载过一篇介绍两个异同点的文章,那个时候还完全不懂react,现在才慢慢开始接触,所以只能总结一些个人的心得,首先自然是react的优点了,个人觉着主要有以 ...
- 微服务之分布式跟踪系统(springboot+pinpoint)
这篇文章介绍一下在微服务(springboot开发)的项目中使用pintpoint监控的过程及效果展示. 背景 随着项目微服务的进行,微服务数量逐渐增加,服务间的调用也越来越复杂,我们急切需要一个AP ...
- [转][CentOS]VI编辑器使用
参考:https://blog.csdn.net/qq_34160679/article/details/79800584 参考:https://www.cnblogs.com/mondol/p/vi ...