混沌分形之朱利亚集（JuliaSet）

朱利亚集合是一个在复平面上形成分形的点的集合。以法国数学家加斯顿·朱利亚（Gaston Julia）的名字命名。我想任何一个有关分形的资料都不会放过曼德勃罗集和朱利亚集。这里将以点集的方式生成出朱利亚集的图形。

关于基类FractalEquation的定义及相关软件见：混沌与分形

class JuliaSet : public FractalEquation
{
public:
    JuliaSet()
    {
        m_StartX = 0.0f;
        m_StartY = 0.0f;
        m_StartZ = 0.0f;

        m_ParamA = -0.75f;
        m_ParamB = 0.01f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        float wx, wy;
        float r;
        float theta;

        float rnd = yf_rand_real(1.0f);

        wx = x-m_ParamA;
        wy = y-m_ParamB;
        if(wx == )
            theta = PI/;
        if(wx > )
            theta = atanf(wy/wx);
        if(wx < )
            theta = PI-atanf(wy/wx); 

        theta = theta/;
        r = sqrtf(wx*wx+wy*wy);

        if(rnd < 0.5f)
            r = sqrt(r);
        else
            r = -sqrt(r);

        outX = r*cos(theta);
        outY = r*sin(theta);
        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}
};

算法中使用了两个参数，修改参数值可以看到不同的图形

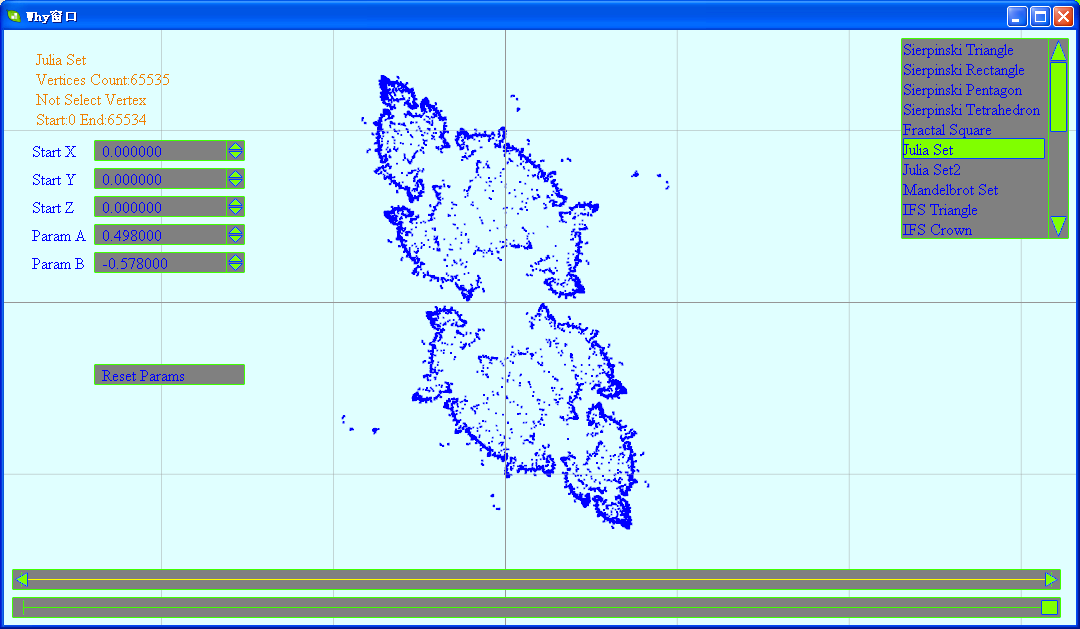
最后发两幅相关图像：

Mandelbrot 图像

Julia Sets图像

……