方差分析、T检验、卡方分析如何区分？

差异研究的目的在于比较两组数据或多组数据之间的差异，通常包括以下几类分析方法，分别是方差分析、T检验和卡方检验。

三个方法的区别

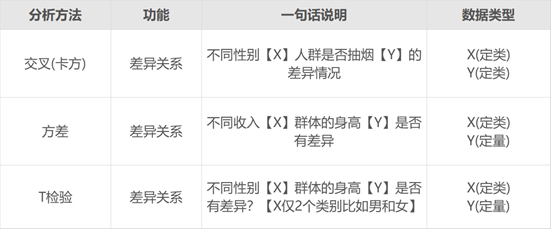
• 其实核心的区别在于：数据类型不一样。如果是定类和定类，此时应该使用卡方分析；如果是定类和定量，此时应该使用方差或者T检验。
• 方差和T检验的区别在于，对于T检验的X来讲，其只能为2个类别比如男和女。如果X为3个类别比如本科以下，本科，本科以上；此时只能使用方差分析。

进一步细分

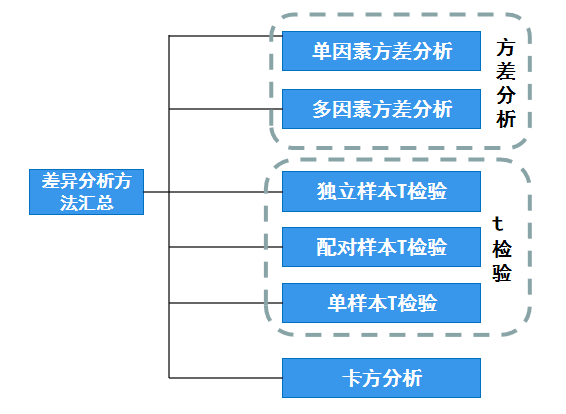
三种方法的具体分类汇总

1）方差分析

根据X的不同，方差分析又可以进行细分。X的个数为一个时，我们称之为单因素方差；X为2个时则为双因素方差；X为3个时则称作三因素方差，依次下去。当X超过1个时，统称为多因素方差。

单因素方差分析,用于分析定类数据与定量数据之间的关系情况。在使用单因素方差分析时，需要每个选项的样本量大于30，比如男性和女性样本量分别是100和120，如果出现某个选项样本量过少时应该首先进行组别合并处理，比如研究不同年龄组样本对于研究变量的差异性态度时，年龄小于20岁的样本量仅为20个，那么需要将小于20岁的选项与另外一组(比如20~25岁)的组别合并为一组，然后再进行单因素方差分析。

如果选项无法进行合并处理，比如研究不同专业样本对于变量的态度差异，研究样本的专业共分为市场营销、心理学、教育学和管理学四个专业，这四个专业之间为彼此独立无法进行合并组别，但是市场营销专业样本量仅为20并没有代表意义，因此可以考虑首先筛选出市场营销专业，即仅比较心理学，教育学和管理学这三个专业对某变量的差异性态度，当对比的组别超过三个，并且呈现出显著性差异时，可以考虑使用事后检验进一步对比具体两两组别间的差异情况。​​​

SPSSAU-方差分析

双因素方差分析,用于分析定类数据(2个)与定量数据之间的关系情况，例如研究人员性别,学历对于网购满意度的差异性;以及男性或者女性时,不同学历是否有着网购满意度差异性;或者同一学历时,不同性别是否有着网购满意度差异性。

SPSSAU-双因素方差分析

多因素方差分析通常用于类实验式问卷研究。比如研究者测试某新药对于胆固醇水平是否有疗效；研究者共招募72名被试，男女分别为36名，以及男女分别再细分使用新药和普通药物；同时高血压患者对于新药可能有干扰，因而研究者将被试是否患高血压也纳入考虑范畴中。因而最终，X共分为三个，分别是药物(旧药和新药)、性别，是否患高血压；Y为胆固醇水平。因而需要进行三因素方差分析即多因素方差分析。

SPSSAU-多因素方差分析

在方法选择上，问卷研究通常会使用方差分析，但某些专业，比如心理学、教育学或者师范类专业等涉及到实验研究时，更多会使用T检验进行分析，另外方差分析与T检验还有较多差异，在某些分析中只能使用其中一种。

2）T检验

T检验共分为三种方法，分别是独立样本T检验，配对样本T检验和单样本T检验。

独立样本T检验和单因素方差分析功能上基本一致，但是独立样本T检验只能比较两组选项的差异，比如男性和女性。相对来讲，独立样本T检验在实验比较时使用频率更高，尤其是生物、医学相关领域。针对问卷研究，如果比较的类别为两组，独立样本T检验和单因素方差分析均可实现，研究者自行选择使用即可。

SPSSAU-t检验分析

独立样本T检验和配对样本T检验功能上都是比较差异，而且均是比较两个组别差异。但二者有着实质性区别，如果是比较不同性别，婚姻状况(已婚和未婚)样本对某变量的差异时，应该使用独立样本T检验。如果比较组别之间有配对关系时，只能使用配对样本T检验，配对关系是指类似实验组和对照组的这类关系。另外独立样本T检验两组样本个数可以不相等，而配对样本T检验的两组样本量需要完全相等。

SPSSAU-配对t检验分析

T检验的第三种分析方法为单样本T检验。比如问卷某题项选项表示为1分代表非常不满意，2分代表比较不满意，3分代表一般，4分代表比较满意，5分代表非常满意，当想分析样本对此题项的态度是否有明显的倾向，比如明显高于3分或者明显低于3分时，即可以使用单样本T检验。单样本T检验是比较某个题项的平均得分是否与某数字(例子是与3进行对比)有着明显的差异，如果呈现出显著性差异，即说明明显该题项平均打分明显不等于3分。此分析方法在问卷研究中较少使用，平均得分是否明显不为3分可以很直观的看出，而不需要单独进行检验分析。

SPSSAU-单样本t检验分析

3）卡方分析

卡方检验用于分析定类数据与定类数据之间的关系情况。例如研究人员想知道两组学生对于手机品牌的偏好差异情况，则应该使用卡方分析。卡方是通过分析不同类别数据的相对选择频数和占比情况，进而进行差异判断，单选题或多选题均可以使用卡方分析进行对比差异分析。

SPSSAU-卡方分析