借助C++探究素数的分布

这里使用的区间是36，144，576，2304，9216，36864，147456，589824，2359296，9437184。至于这个区间是怎么得到的，感兴趣的同鞋可前往（https://www.cnblogs.com/chanji/p/12808117.html）观看。

首先附上程序：

#include <iostream>
#include <cmath>
using namespace std;
int isPrime(int n);
const int n = 9437184;//左区间
const int m = 37748736;//右区间
int main() {
    int count = 0;
    for(int i = n;i <= m;++i) {
        if(isPrime(i)) {
            ++count;
        }
    }
    cout << count << endl;
    return 0;
}

int isPrime(int n) //判断一个数是否为素数的函数
{    if(n < 2) return false;
     for(int i = 2; i <= sqrt(n); i++) {
        if((n % i) == 0) // 如果能被除了1和它本身的数整除，就不是素数
            return false;

    }
    return true; // 是素数
}

得到的结果是：23，71，237，800，2766，9723，34703，125174，456172。

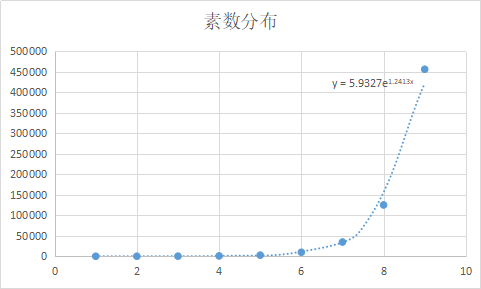
发现得到的点是可以用指数拟合的。