【线型DP模板】最上上升子序列（LIS），最长公共子序列（LCS），最长公共上升子序列（LCIS）

BEGIN

---

LIS：

一个数的序列bi，当b1 < b2 < … < bS的时候，我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN)，我们可以得到一些上升的子序列(ai1, ai2, …, aiK)，这里1 <= i1 < i2 < … < iK <= N。比如，对于序列(1, 7, 3, 5, 9, 4, 8)，有它的一些上升子序列，如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4，比如子序列(1, 3, 5, 8).

输入样例 7

　　　　 2 5 3 4 1 7 6

输出样例 4

1.上升序列： //???这里怎么格式这么丑，还调不了

这道题中就是在当前序列删去几个数，使剩下的几个数构成一个从小到大的序列，例如：2 3 4 6和2 4 7都是上升序列.

2.具体思路：

设定一个一维数组f[i]，表示从1到i的最大上升子序列长度，所以f数组中的每一个数都应该初始化为1，因为一个数本身的长度就是1，我们可以让原数组a中的每一个数依次与它前面的所有数进行比较，如果当前的a[i]>a[j]且当前的f[i]大于f[j]，那么我们的f[i]就可以从f[j]转移过来，新得到的f[i]就是f[j]的大小加上1，于是我们就得到了我们动归中的第一个转移方程：f[i]=max(f[j]+1)(i>j&&a[i]>a[j])，时间效率：O(n*n)

3.主代码：

     for(int i=;i<=n;i++){
         for(int j=;j<i;j++){//j严格小于i，否则可能会WA
             if(a[i]>a[j]&&f[i]<f[j]+){//一般比较时要写的是f[i]<f[j]+1而不是f[i]<=f[j]
                 f[i]=f[j]+;
                 dp[i]=j;//记录路径的，下面会说路径输出
                 ans=max(ans,f[i]);
             }
         }
     }

4.优化：//正常人用二分优化，不正常的人用树形优化，用树形优化的估计也用指针建树

对于一个上升子序列，其结尾元素越小肯定以后能插入的元素越多，子序列的长度也就越大，这里我们抛弃数组f，新建一个数组low，low[i]表示长度为i的LIS结尾元素的最小值。对于一个新的数，如果这个数比当前序列末尾元素要大，那肯定是要插在队尾，如果不大于的话，就需要找到low数组中第一个大于这个数的位置并替换掉，如此一来就能够插入尽量多的元素，而时间效率为O(n*logn)，如图：

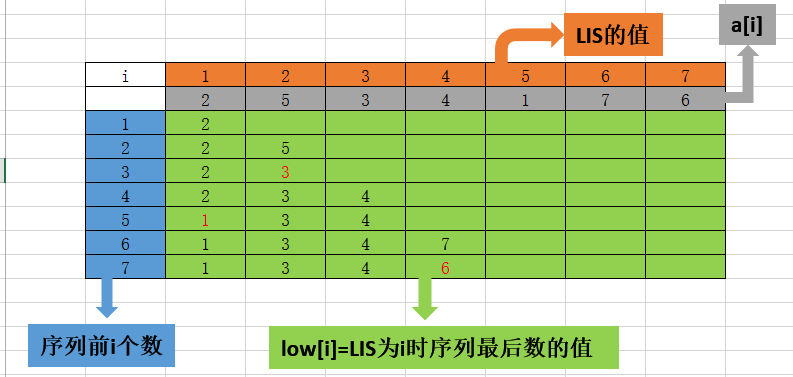
代码如下：

     low1[]=a[];//长度为1的序列最后一个元素一开始肯定是原序列的第一个数
     for(int i=;i<=n;i++){
     if(low1[ans1]<a[i])low1[++ans1]=a[i];
     else low1[lower_bound(low1+,ans1++low1,a[i])-low1]=a[i];
     }//low_bound函数可以帮助我们快速找到第一个大于某数的位置
       //而upper_bound可以帮助我们快速找到第一个大于等于某数的位置
       //原理都是二分，用法如代码中的那样

5.路径记录:懒得写了，等以后有时间再写

6.友情例题链接：友好城市：https://www.cnblogs.com/614685877--aakennes/p/12659005.html

　　　　　　　　导弹拦截：没写

　　　　　　　　打地鼠：没写

---

LCS:

子序列:一个序列A ＝ a1,a2,……an,中任意删除若干项，剩余的序列叫做A的一个子序列。也可以认为是从序列A按原顺序保留任意若干项得到的序列。

公共子序列:顾名思义，如果序列C既是序列A的子序列，同时也是序列B的子序列，则称它为序列A和序列B的公共子序列。空序列是任何两个序列的公共子序列。

最长公共子序列:A和B的公共子序列中长度最长的（包含元素最多的）叫做A和B的公共子序列。

输入样例：8 6

　　　　　1 3 5 4 2 6 8 7

　　　　　1 4 8 6 7 5

输出样例：4

hint:最长公共子序列有两个分别是： 1 4 8 7 ，1 4 6 7

1.如果暴力枚举，把两个序列中的数都扫一遍，序列一有2n个子序列，序列二有2m个子序列,时间效率为O(2^(m+n)).

2.定义二维数组f，f[i][j]变数为序列1前i个数，序列2中前j个数的LCS，如图所示f[i][j]如果a[i]!=a[j]，那么f[i][j]会从它上一个或左一个中的最大值直接转移，如果a[i]==a[j]那么它会从左上角转移过来，值为f[i-1][j-1]+1（应该没人会问为什么不是从上或从下转移的吧，实在不懂就看图）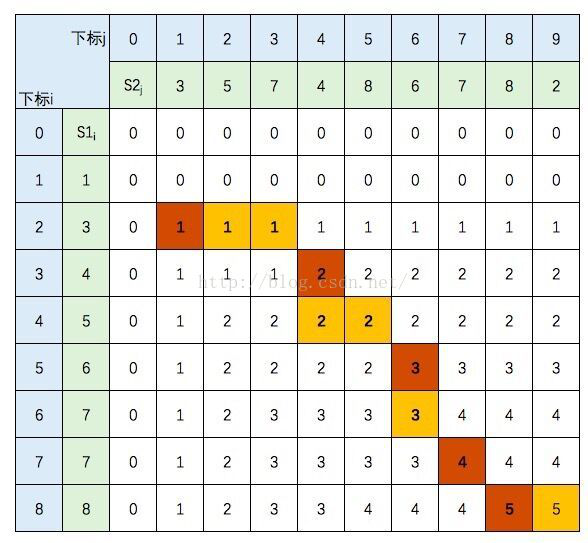

---

时间：4.9夜里11点，溜了溜了

---

时间：4.11早上19丶 

在多科积累本的压榨下，终于抽出时间来更新了（其实有没写完的，明天再说）

---

3.状态转移方程：f[i][j]=max(f[i-1][j],f[i][j-1])(a[i]!=a[j]) f[i][j]=f[i-1][j-1]+1(a[i]==a[j])

4.代码：

未优化：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 using namespace std;
 const int maxn=1e3+,INF=0x3f3f3f3f;
 int n,len1,len2,f[maxn][maxn],a1[maxn],a2[maxn];
 int main(){
     freopen("a.in","r",stdin);
     cin>>len1>>len2;
     for(int i=;i<=len1;i++)cin>>a1[i];
     for(int i=;i<=len2;i++)cin>>a2[i];
     int ans=;
     for(int i=;i<=len1;i++){
         for(int j=;j<=len2;j++){
             if(a1[i]==a2[j])f[i][j]=f[i-][j-]+;
             else if(a1[i]!=a2[j])f[i][j]=max(f[i-][j],f[i][j-]);
             ans=max(ans,f[i][j]);
         }
     }
     cout<<ans;
     return ;
 }

滚动数组优化版本：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 using namespace std;
 const int maxn=1e3+,INF=0x3f3f3f3f;
 int n,len1,len2,f[maxn][maxn],a1[maxn],a2[maxn];
 int main(){
     freopen("a.in","r",stdin);
     cin>>len1>>len2;
     for(int i=;i<=len1;i++)cin>>a1[i];
     for(int i=;i<=len2;i++)cin>>a2[i];
     int ans=,k=;
     for(int i=;i<=len1;i++){
         k=!k;
         for(int j=;j<=len2;j++){
             if(a1[i]==a2[j])f[k][j]=f[!k][j-]+;//正常滚动数组，用i%2也行
             else if(a1[i]!=a2[j])f[k][j]=max(f[!k][j],f[k][j-]);
             ans=max(ans,f[k][j]);
         }
     }
     cout<<ans;
     return ;
 }

5.路径记录

回看之前那张图，褐色的正好是其种的一种序列，都是从左上转移过来，所以我们只需开一个二维数组记录下转移状态，然后递归输出即可（其实也可以用滚动数组优化）

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 using namespace std;
 const int maxn=1e3+,INF=0x3f3f3f3f;
 int n,len1,g[maxn][maxn],len2,f[maxn][maxn],a1[maxn],a2[maxn];
 void Print(int i,int j){
     if(i==||j==)return;
     if(g[i][j]==)Print(i-,j-),cout<<a1[i]<<" ";
     if(g[i][j]==)Print(i-,j);
     if(g[i][j]==-)Print(i,j-);
 }
 int main(){
     freopen("a.in","r",stdin);
     cin>>len1>>len2;
     for(int i=;i<=len1;i++)cin>>a1[i];
     for(int i=;i<=len2;i++)cin>>a2[i];
     int ans=,k=;
     for(int i=;i<=len1;i++){
         //滚动数组大变样 
         for(int j=;j<=len2;j++){
             if(a1[i]==a2[j])f[i%][j]=f[(i-)%][j-]+,g[i][j]=;//0表示左上 
             else if(f[i-][j]>=f[i%][j-])f[i%][j]=f[(i-)%][j],g[i][j]=;//1表示正上
             else f[i%][j]=f[i%][j-],g[i][j]=-;//-1表示正左 
             ans=max(ans,f[k][j]);
         }
     }
     cout<<ans;
     return ;
 }//嘤嘤嘤，编译过了，但不保证A

6.友情例题链接：Prince and Princess 王子和公主：https://www.cnblogs.com/614685877--aakennes/p/12663440.html

LCIS：

两个整数序列，{a1,a2...,am},{b1,b2...,bn},求两序列最长公共上升子序列长度。

//怎么粘贴过来变成图片了？

1.LCIS显然是LIS和LCS的并查集，不对，是交集（并查集题做多了），定义二维数组f，f[i][j]表示第一个序列前i个元素，第二个序列前j个元素且以b[j]结束的LCIS，两个序列最后的元素为a[i]、b[j]。如果a[i]!=b[j]，f[i][j]=f[i-1][j]，因为此时以b[j]结尾的LCIS有没有a[i]结果是一样的；相反，如果a[i]==b[j]，此时f[i][j]=max(f[i-1][k])+1。（从老师那里搬过来的课件有丶混乱，还是代码好理解丶）

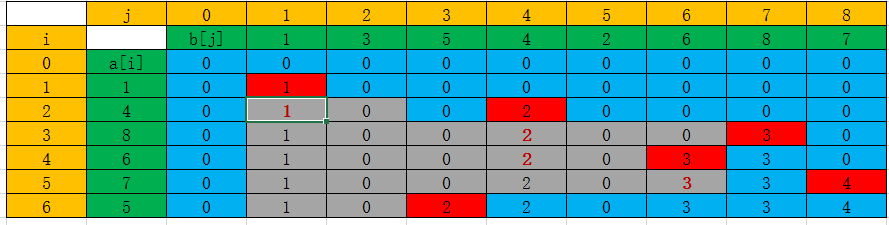
2.代码:

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 using namespace std;
 const int maxn=1e3+,INF=0x3f3f3f3f;
 int n,len1,g[maxn][maxn],len2,f[maxn][maxn],a1[maxn],a2[maxn];
 int main(){
     freopen("a.in","r",stdin);
     cin>>len1>>len2;
     for(int i=;i<=len1;i++)cin>>a1[i];
     for(int i=;i<=len2;i++)cin>>a2[i];
     int ans=,k=;
     for(int i=;i<=len1;i++){
         ans=;
         for(int j=;j<=len2;j++){
             if(a[i]>b[j]&&ans<f[j])ans=f[j];
             if(a[i]==b[j])f[j]=ans+;
         }
     }
     cout<<ans;
     return ;
 }//嘤嘤嘤

---

终于写完了，写了两三个小时