Poj-P1088题解【动态规划/记忆化搜索】

本文为原创，转载请注明：http://www.cnblogs.com/kylewilson/

题目出处：

http://poj.org/problem?id=1088

题目描述：

区域由一个二维数组给出。数组的每个数字代表点的高度。如下：

1 2 3 4 5 
16 17 18 19 6 
15 24 25 20 7 
14 23 22 21 8 
13 12 11 10 9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。

输入：

输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行，每行有C个整数，代表高度h，0<=h<=10000。

5 5

1 2 3 4 5

16 17 18 19 6

15 24 25 20 7

14 23 22 21 8

13 12 11 10 9

思路分析：

首先考考虑最终的目标状态，即已经找到了一条最大长度的滑坡，如下图：

绿色为起点，红色为终点；

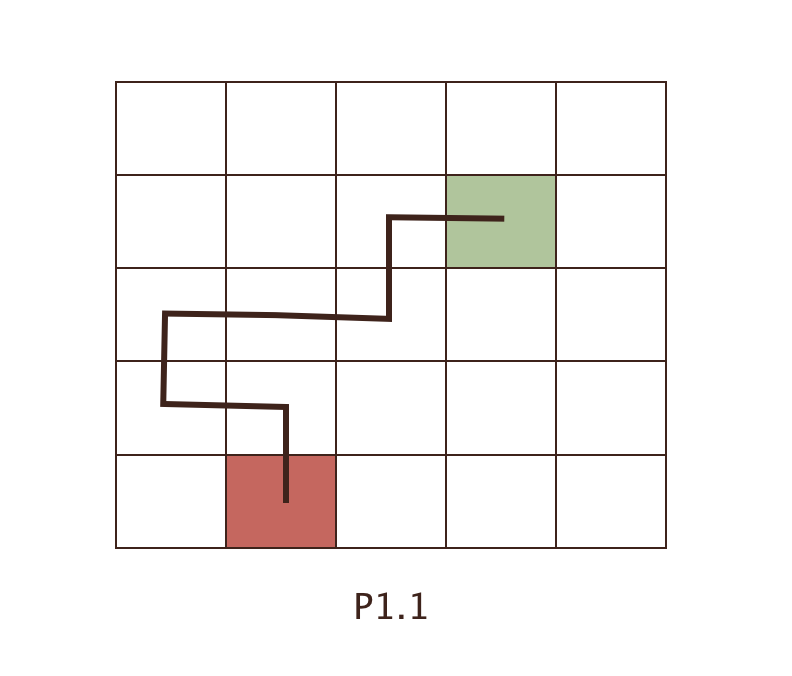
可滑行的条件是高度递减，即原问题变为：在一个图中，找出从一个点到另一个占依次递减的最长路径。

貌似是一个搜索问题，用BFS或者DFS很容易搞定，即从一个点向4个方向搜索，直到无路可走，找出最长的路径。

这样需要枚举每一个点作为起点，发现之前很多的点已经搜索过了，还会继续搜索，重复计算，浪费时间。

所以此时要利用动态规划的思想，计算子问题结果，避免重复计算。

DFS+DP，也就是记忆化搜索，如果某一个点已经搜索过了，直接返回结果而不需要再搜索。

用f[i][j]表示以(i, j)为终点最长的滑坡长度

则状态转移如下：

f[i][j]=max(dfs(x,y)+1)，其中(x,y)为(i,j)的4个方向上的点，并且高度递减

提示：

处理方向时可以提前定义一个常量2维数组，即方向向量，枚举时加上向量即可

C++源码如下：

github: https://github.com/Kyle-Wilson1/Poj/tree/master/P1088

#include <iostream>
#include <fstream>
#include <vector>

using namespace std;

const int direction[4][2] = {{0,  -1},
                             {0,  1},
                             {1,  0},
                             {-1, 0}};

int maxOfTwo(int a, int b) {
    return a > b ? a : b;
}

int solve(vector<vector<int>> &snowMountain, vector<vector<int>> &f, int i, int j, int r, int c) {
    int x, y;
    if (f[i][j] != -1)
        return f[i][j];

    f[i][j] = 1;
    for (int k = 0; k < 4; k++) {
        x = i + direction[k][0];
        y = j + direction[k][1];

        //valid direction
        if (x >= 0 && x < r && y >= 0 && y < c && snowMountain[i][j] > snowMountain[x][y]) {
            f[i][j] = maxOfTwo(f[i][j], solve(snowMountain, f, x, y, r, c) + 1);
        }
    }
    return f[i][j];
}

int main() {

    ifstream fin("a.in");
    ofstream fout("a.out");

    int i, j, r, c, maxHeight = 0;

    fin >> r >> c;

    vector<vector<int>> snowMountain(r, vector<int>(c, 0));
    vector<vector<int>> f(r, vector<int>(c, -1));

    for (i = 0; i < r; i++)
        for (j = 0; j < c; j++)
            fin >> snowMountain[i][j];

    for (i = 0; i < r; i++)
        for (j = 0; j < c; j++) {
            maxHeight = maxOfTwo(maxHeight, solve(snowMountain, f, i, j, r, c));
        }

    fout << maxHeight << endl;

    fin.close();
    fout.close();
    return 0;
}