POJ 2309：BST lowbit

BST

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 9140		Accepted: 5580

Description

Consider an infinite full binary search tree (see the figure below), the numbers in the nodes are 1, 2, 3, .... In a subtree whose root node is X, we can get the minimum number in this subtree by repeating going down the left node until the last level, and
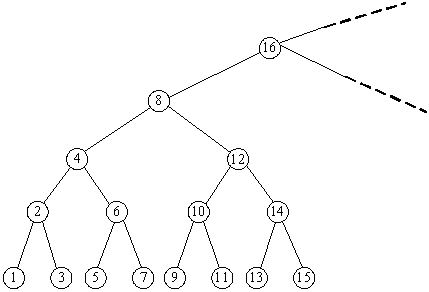
we can also find the maximum number by going down the right node. Now you are given some queries as "What are the minimum and maximum numbers in the subtree whose root node is X?" Please try to find answers for there queries. 

Input

In the input, the first line contains an integer N, which represents the number of queries. In the next N lines, each contains a number representing a subtree with root number X (1 <= X <= 2³¹ - 1).

Output

There are N lines in total, the i-th of which contains the answer for the i-th query.

Sample Input

2
8
10

Sample Output

1 15
9 11

发现每个点含有的节点数量就是做树状数组时lowbit()的值,lowbit()就是一个数x在二进制表示下最右边的那个1保留，其余值全部赋值为0的二进制数。

简单表示就是x&(x^(x-1))=x&(-x)。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#pragma warning(disable:4996)
using namespace std;  

const int N = 32005;  

int c[N],a[N],n;  

int lowbit(int x)
{
    return x & (-x);
}  

int main()
{
	int i,query;
	long long ask;
	scanf("%d",&query);

	for(i=1;i<=query;i++)
	{
		cin>>ask;
		cout<<ask-(lowbit(ask)-1)<<" "<<ask+(lowbit(ask)-1)<<endl;
	}
    return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。