leetcode（数据结构）—— 镜像二叉树

镜像二叉树，力扣上面的的题目，这道题很简单，放出来的原因是它要求用两种解法来写这道题——递归和迭代，而且数据结构学到了树，记录自己学习的过程，以免忘了，没地方找。

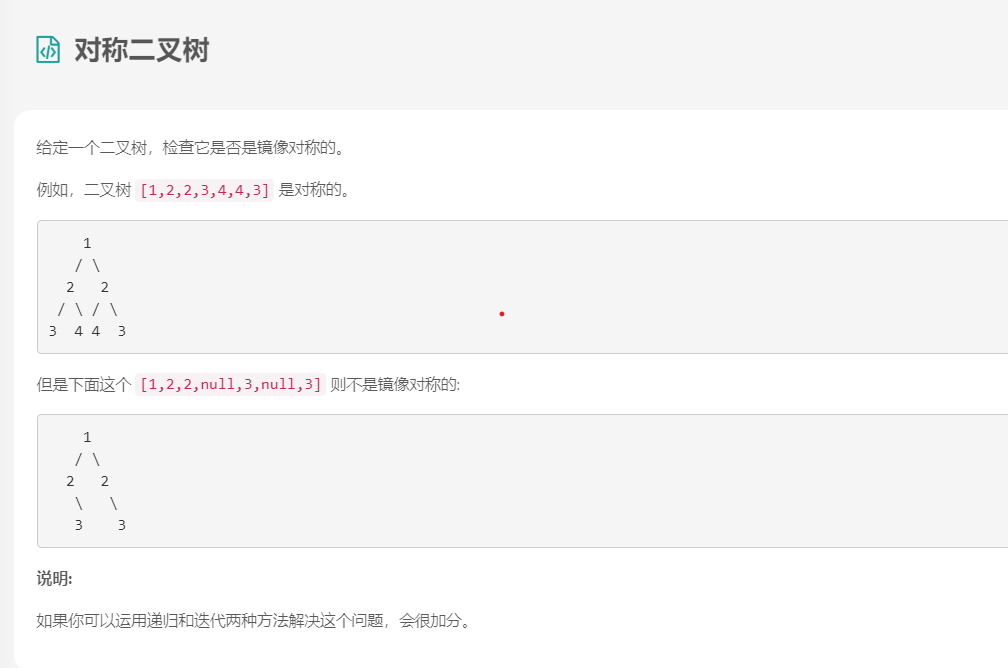
题目的意图很明显，就是然你写个程序看看是不是对称的，对称的条件很明显：

//左子树点值等于右子树的值
        LeftChild->val == RightChild->val
    

　　然后我们想一想什么样的树被称为镜像对称？

是不是当一个树的左子树与右子树镜像对称，那么这个树是对称的。那么问题是不是可以转化成：两个树在什么情况下互为镜像？

　　很明显

当子树相互对称应该符合一下条件：

　　1、它们的两个根结点具有相同的值。

　　2、每个树的右子树都与另一个树的左子树镜像对称。

//力扣给的结构体
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

；现在让我来想想递归如何实现

　　1、递归就会有终止条件，那么这个函数什么时候表示递归结束呢？

　　　　当然是到达树的这一分支的最大深度。那么如何检测递归到了树的这一分支的最大深度，很显然每一棵二叉树，如果它不是根节点，那么，当该节点的左右子树都为空时，表示这树的这一支就兜底了。

　　　　由于这是镜像二叉树的题而不是测深度，所以我们返回的条件有三种：

　　　　第一种，两个节点都为空，返回 true；

　　　　第二种，两个节点不都为空 ，返回 false；

　　　　第三种，两个节点的值不相等，返回 false；

得出了终止条件递归就基本成型了，就剩下迭代了，迭代这个较为简单，不在这里赘述了。

贴代码：

　　

bool CheckVal(struct TreeNode* LeftChild, struct TreeNode* RightChild)
{
    if (NULL == LeftChild && NULL == RightChild)
    {
        return true;
    }
    if (NULL == LeftChild || NULL == RightChild)
    {
        return false;
    }
    return (LeftChild->val == RightChild->val) && CheckVal(LeftChild->left, RightChild->right) && CheckVal(LeftChild->right, RightChild->left);
}

bool isSymmetric(struct TreeNode* root){
    if (NULL == root)
    {
        return true;
    }
    return CheckVal(root->left, root->right);
}

　　迭代就不做细说了，这个实现起来太简单了，BFS略微改改就行了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
#define MAXSIZE 1024

bool isSymmetric(struct TreeNode* root){
    struct TreeNode *Queue[MAXSIZE];
    int index = ;
    Queue[index++] = root;
    Queue[index++] = root;

    while ( != index)
    {
        struct TreeNode *leftChild = Queue[--index];
        struct TreeNode *rightChild = Queue[--index];

        if (NULL == leftChild && NULL == rightChild)
        {
            continue;
        }
        if ((NULL == leftChild || NULL == rightChild) || (leftChild->val != rightChild->val))
        {
            return false;
        }

        Queue[index++] = leftChild->left;
        Queue[index++] = rightChild->right;
        Queue[index++] = leftChild->right;
        Queue[index++] = rightChild->left;
    }
    return true;
}

　　好吧，我这个更像栈一点。

算法不易，诸君共勉！