Rikka with Prefix Sum

Rikka with Prefix Sum

题目

https://www.nowcoder.com/acm/contest/148/D

题目有三个操作

1. l到r都添加一个数
2. 取一次前缀和
3. 查询区间和

这三个操作实际上都跟求前缀和有关。

如果把操作2当作时间戳 进行一次操作2时间就加一，而操作一相当于时间-1的时候对l点加w，对r+1点加-w。而查询操作就相当于时间+1的时候query(r)-query(l-1)。

那求前缀和该怎么做呢？刚开始我想的是用树状数组，但是要求很多次前缀和，复杂度不允许。我们可以打个表找一下规律。

若在某点添加1

time	a1	a2	a3	a4
0 add	1	0	0	0
1	1	1	1	1
2	1	2	3	4
3	1	3	6	10
4	1	4	10	20
5 query	1	5	15	35

看上去是不是很眼熟：

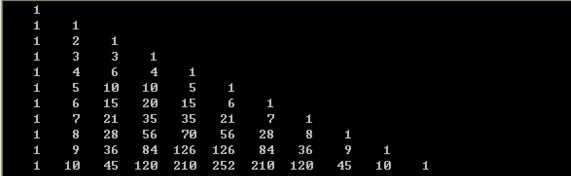
相当于倾斜45°的杨辉三角

然后找出规律



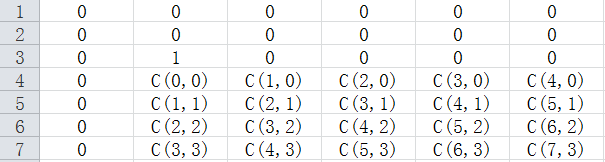
于是：单点修改对一点贡献度为

C(L+T-1,T-1) * V

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=998244353;
const int maxn=1e5+7;
ll inv[maxn<<1],fac[maxn<<1];
template<class T>
void read(T &res)
{
    res=0;
    char c=getchar();
    T f=1;
    while(c<'0'||c>'9'){
        if(c=='-') f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        res=res*10+c-'0';
        c=getchar();
    }
    res*=f;
}
ll qpow(ll x,ll n){
    ll ret=1;
    x%=mod;
    while(n){
        if(n&1) ret=ret*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return ret;
}
void init()
{
    int N=maxn*2;
    fac[0]=1;
    for(int i=1;i<N;i++){
        fac[i]=fac[i-1]*i%mod;
    }
    inv[N-1]=qpow(fac[N-1],mod-2);
    for(int i=N-2;i>=0;i--){
        inv[i]=inv[i+1]*(i+1)%mod;
    }
}
ll c(int n,int k)
{
    if(k>n||k<0) return 0;
   return fac[n]*inv[k]%mod*inv[n-k]%mod;
}
struct node
{
    int time;
    int val;
    int id;
}s[maxn];
int tol;
ll query(int a,int b)
{
    ll ans=0;
    for(int i=0;i<tol;i++){
        if(s[i].time<=a&&s[i].id<=b)
        {
            ans=(ans+c(a-s[i].time+b-s[i].id-1,a-s[i].time-1)*s[i].val%mod)%mod;
        }
    }
    return ans;
}
int main()
{
    int t;
    read(t);
    init();
    while(t--){
        int n,m,op,l,r,w;
        read(n);
        read(m);
        tol=0;
        int cur=1;
        for(int i=1;i<=m;i++){
        read(op);
        if(op==1){
            read(l),read(r),read(w);
            s[tol].id=l,s[tol].val=w%mod ,s[tol].time=cur-1;
            tol++;
            s[tol].id=r+1,s[tol].val=-w%mod ,s[tol].time=cur-1;
            tol++;
        }
        else if(op==2) cur++;
        else if(op==3){
            read(l);
            read(r);
            ll ans=query(cur+1,r)-query(cur+1,l-1);
            ans=(ans%mod+mod)%mod;
            printf("%lld\n",ans);
        }
        }
    }
    return 0;
}