Hardy-Weinberg laws

I.3 Diploids with two alleles: Hardy-Weinberg laws

假设子代是Aa，AA，aa的概率分别是PAa，PAA，Paa，A的基因概率是P1，a的基因概率是P2（可以利用基因的数量来理解）

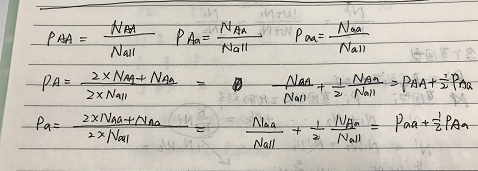
（P1也是配子A的概率，P2也是配子a的概率，因为在单倍体阶段等于把二倍体（两套遗传信息的组合）拆开，看到每个基因的所有等位基因）：

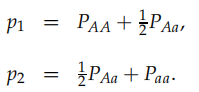
random mating of individuals gave the same results as random combination of the pool of gametes

因为：

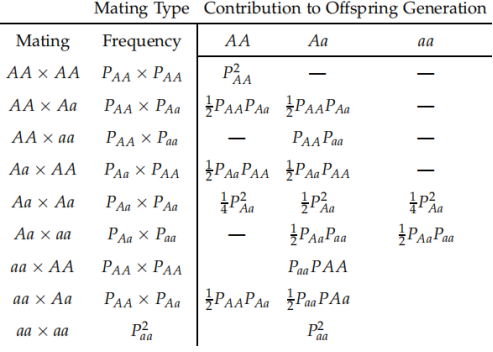
合并同类项得到：

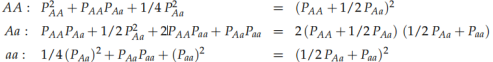
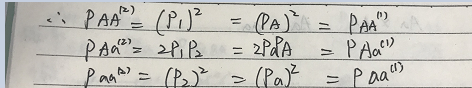
所以发现：

1,每一代配子chance（基因频率）一致

1. 每一代二倍体chance（基因型频率）一致

所以得到Hardy-Weinberg Law：

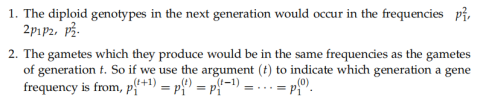
因为基因频率和基因型频率之间的关系，我们可以分析基因频率从而分析基因型频率（law 1），孟德尔复制并无繁殖力偏向性（law2）

使用哈代公式有一些前提（因为推导之前的便提到了一些前提条件（这些条件是为了有稳定的基因型））

1. 随机交配
2. 等位基因无繁殖力和差异
3. 等位基因无性别差异
4. 子代无突变
5. 子代全由亲代产出
6. 无迁移（迁移：亲代时期有A1，A2两种等位基因，但是子代时期有A2,A3,A4三种等位基因）
7. 所有个体无生存力差异（因为这会造成老中青三类生物的基因频率发生改变）
8. 大种群（大数据可以使用数学规律来估计（孟德尔））