SPOJ687 Repeats

本篇是罗穗骞《后缀数组——处理字符串的有力工具》的读书笔记。

知识点：　　后缀数组、RMQ

解题思路：

　　枚举长度 \(L\)，然后检查长度为 \(L\) 的子串最多能连续重复几次。

　　对于给定的字符串 \(S\)，我们只关注其上坐标为 \(0, L, 2L, ......\) 的点。

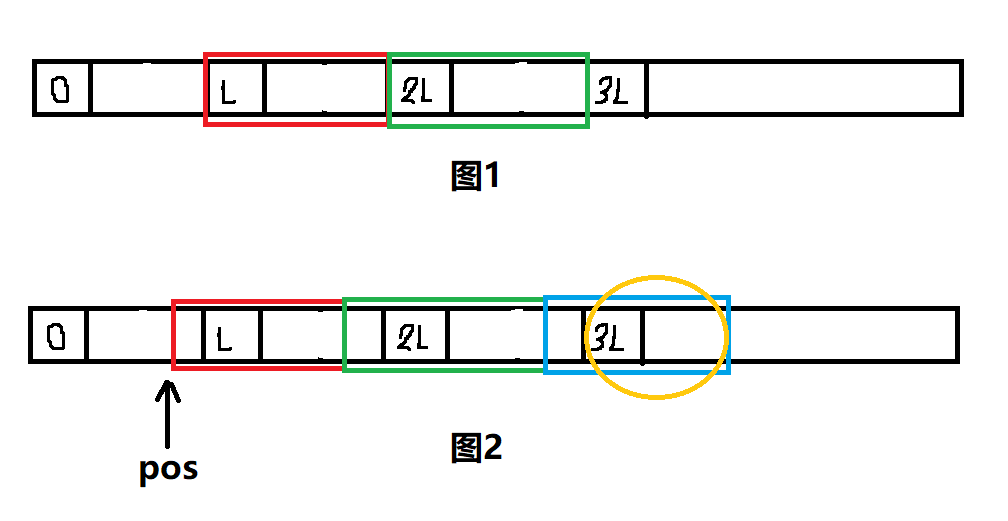
　　如果连续重复子串的首字符恰好在这些点上，那么连续重复子串出现的次数恰好是 \( \frac{lcp(L_1, L_2)}{L} + 1\)，(注：\(lcp\) 为 Longest Common Prefix 的简写），如图 1 所示；

　　否则，我们先计算出 \(lcp(L_1, L_2)\) 中 模 \( L\) 后余下的长度 \(L'\)，如图 2 中橙色圈里的片段，可以推测出连续重复子串真正的首字符位于 \( pos = L_1 - (L - L')\)，如果 \(0 \le pos\)，则连续重复子串出现的次数为：\( \frac{lcp(pos, pos+L)}{L} + 1\)。

　　记录出现的最多次数，即为答案。最长公共前缀的查询要用 RMQ 优化。

AC代码：

 #include <iostream>
 #include <cstdio>
 #include <algorithm>

 using namespace std;
 const int maxn =  + , inf = 0x7fffffff;
 int len, tk;
 int Rank[maxn], tmp[maxn];
 int S[maxn];
 int sa[maxn], lcp[maxn];

 bool compare_sa(int i, int j) {
     if (Rank[i] != Rank[j])    return Rank[i] < Rank[j];
     else {
         int ri = i + tk <= len ? Rank[i + tk] : -;
         int rj = j + tk <= len ? Rank[j + tk] : -;
         return ri < rj;
     }
 }

 void construct_sa() {
     for (int i = ; i <= len; i++) {
         sa[i] = i;
         Rank[i] = i < len ? S[i] : -;
     }

     for (tk = ; tk <= len; tk *= ) {
         sort(sa, sa + len + , compare_sa);
         tmp[sa[]] = ;
         for (int i = ; i <= len; i++) {
             tmp[sa[i]] = tmp[sa[i - ]] + (compare_sa(sa[i - ], sa[i]) ?  : );
         }
         for (int i = ; i <= len; i++) {
             Rank[i] = tmp[i];
         }
     }
 }

 void construct_lcp() {
     int h = ;
     lcp[] = ;
     for (int i = ; i < len; i++) {
         int j = sa[Rank[i] - ];

         if (h > )    h--;
         for (; j + h < len && i + h < len; h++) {
             if (S[j + h] != S[i + h])    break;
         }
         lcp[Rank[i] - ] = h;
     }
 }

 int RMQ[maxn];
 int mm[maxn], best[][maxn];
 void initRMQ(int n) {
     mm[] = -;
     for (int i = ; i <= n; i++)
         mm[i] = ((i&(i - )) == ) ? mm[i - ] +  : mm[i - ];
     for (int i = ; i <= n; i++)    best[][i] = i;
     for (int i = ; i <= mm[n]; i++) {
         for (int j = ; j + ( << i) -  <= n; j++) {
             int a = best[i - ][j];
             int b = best[i - ][j + ( << (i - ))];
             if (RMQ[a] < RMQ[b])    best[i][j] = a;
             else
             {
                 best[i][j] = b;
             }
         }
     }
 }
 int askRMQ(int a, int b) {
     int t;
     t = mm[b - a + ];
     b -= ( << t) - ;
     a = best[t][a];    b = best[t][b];
     return RMQ[a] < RMQ[b] ? a : b;
 }
 int find_lcp(int a, int b) {
     if (a>b) swap(a, b);
     return lcp[askRMQ(a, b - )];
 }
 int main()
 {
     char inp[];
     int H;
     scanf("%d", &H);
     while (H--) {
         scanf("%d", &len);
         for (int i = ; i<len; i++) {
             scanf("%s", inp);
             if (inp[] == 'a') S[i] = ;
             else    S[i] = ;
         }
         construct_sa();
         construct_lcp();
         for (int i = ; i <= len; i++)    RMQ[i] = lcp[i];
         initRMQ(len);
         int ans = ;
         for (int i = ; i <= len; i++) {
             int ret = ;
             for (int j = ; j + i<len; j += i) {
                 int r1 = Rank[j], r2 = Rank[j + i];
                 int L = find_lcp(r1, r2);
                 int temp = L / i + ;
                 int k = j - (i - L%i);
                 if (k >= ) {
                     temp = find_lcp(Rank[k], Rank[k + i]) / i + ;
                 }
                 ret = max(ret, temp);
             }
             ans = max(ans, ret);
         }
         printf("%d\n", ans);
     }
     return ;
 }