【刷题】洛谷 P4143 采集矿石

题目背景

ZRQ成功从坍塌的洞穴中逃了出来。终于，他看到了要研究的矿石。他想挑一些带回去完成任务。

题目来源：Zhang_RQ哦对了ZRQ就他，嗯

题目描述

ZRQ发现这里有 \(N\) 块排成一排的矿石。

他用一个小写字母来表示每块矿石，他还发现每块矿石有一个重要度 \(V_i\)​

ZRQ想采集一段连续的矿石回研究所。

他非常严格，被采集的一段矿石必须满足小写字母的字典序降序排名等于这段矿石的重要度和。

这里多个出现在不同位置的本质相同串的字典序排名相同。

比如说字母串为 aa，那么第一个a的排名和第二个a的排名相同，都是2（第1是aa）。

ZRQ问你，在原串中有哪些不同的子串可以被采集？

这里子串不同定义为出现位置不同，也就是说本质相同的子串出现在不同位置都要计算一次（当然重要度和等于排名是前提）。

比如共有 \(4\) 块矿石，小写字母串为abcd，重要度各为10 0 1 1

我们把所有的子串按照字典序从大到小排名：1:d 2:cd 3:c 4:bcd 5:bc 6:b 7:abcd 8:abc 9:ab 10:a

那么串d的排名为 \(1\) （第一大），重要度和为 \(1\) ，可以被采集。

串cd的排名为 \(2\) ，重要度和为 \(2\) ，可以被采集。

串a的排名为 \(10\) ，重要度和为 \(10\) ，可以被采集。

其他串则不满足这个条件，故有三个串可以被采集。

输入输出格式

输入格式：

第一行一个长度为 \(N\) 由小写字母组成的字符串，每个字符代表一个矿石

第二行 \(N\) 个整数，表示 \(V_i\)​

输出格式：

一行一个整数，表示能被采集的子串个数 \(S\)

接下来 \(S\) 行每行两个整数 \(L,R\) ，分别表示每个可采集子串的左端点与右端点，按照左端点升序为第一关键字，右端点升序为第二关键字排序。

输入输出样例

输入样例#1：

abcd

10 0 1 1

输出样例#1：

3

1 1

3 4

4 4

输入样例#2：

aaaa

1 1 1 1

输出样例#2：

0

输入样例#3：

aaa

1 1 1

输出样例#3：

2

1 2

2 3

输入样例#4：

aaa

1 1 2

输出样例#4：

1

1 2

说明

共 \(10\) 个测试点，每个点 \(10\) 分，计 \(100\) 分。

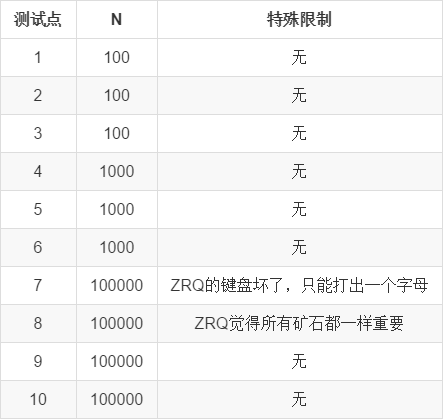
对于测试点 \(1\) ~ \(6\) ，时间限制为 \(1s\) 。

对于测试点 \(7\) ~ \(10\) ，时间限制为 \(2s\) 。

对于所有测试点，有 \(0 \le V_i \le 1000\) ，保证每个点可被采集的子串不超过 \(100000\) 个。

样例#1解释放在题面里了。

样例#2解释：

每个子串都不满足条件。

串a的排名是 \(4\) ，重要度和都是 \(1\) 。

串aa的排名是 \(3\) ，重要度和都是 \(2\) 。

串aaa的排名是 \(2\) ，重要度和都是 \(3\) 。

串aaaa的排名是 \(1\) ，重要度和都是 \(4\) 。

样例 #3解释：

串a的排名是 \(3\) ，重要度和都是 \(1\) 。

串aa的排名是 \(2\) ，重要度和都是 \(2\) ，共有两个串aa，位置分别为 \(1\) ~ \(2\) 和 \(2\) ~ \(3\) 。

串aaa的排名是 \(1\) ，重要度和都是 \(3\) 。

样例 #4解释：

可以发现，串 \(2\) ~ \(3\) （第二个aa）不满足条件了。它的排名还是 \(2\) 不变，但是重要度和为 \(3\) 。

题解

SA+线段树

转换一下考虑每个子串的方法

因为一个字符串的每一个后缀的前缀都是原串的一个子串，所以从后缀方面考虑

对于一个后缀，看它的前缀（即一个子串）。这个前缀越长，那么权值之和就越大，但是倒序排名就越小（写写看），即这两个值随前缀的长度，一个上升，一个下降。

这样的两条线只会有一个交点。又由于这其实并不是两条线，而是两堆点构成的虚线，所以还不一定有交点。

于是我们知道，对于一个后缀，至多只有一个它的前缀满足题目条件。题目数据范围中每个点可被采集的子串的最大值与字符串的长度相同也暗示了这个性质。

那么枚举后缀，二分两条虚线的交点（暂时当做有交点），那么我们需要快速得知一段长度的权值和与某个后缀的前缀在所有子串中的字典序倒序排名。

权值和直接前缀和就好了，很简单；关键在于找排名。

对字符串求SA与height，那么找一个后缀和前缀的rk，先找到在SA中这个前缀最早出现的位置。从当前后缀在SA中的位置开始寻找，一直找到height值小于我们的后缀的前缀的长度的位置，其对应的两个后缀中后面那个就是SA中这个前缀最早出现的位置。

于是可以用线段树维护height数组，方便这个rk位置的查询

找到位置后，类似求本质不同子串的方法。对于一个后缀，它的所有前缀代表的子串在所有子串的排名一定是连续的一段，并且也是按照SA的顺序来的（画一画就知道为什么了）。

那么就可以当做求本质不同子串，一个后缀 \(i\) 能够造成的新子串的贡献是 \(n-SA[i]+1-height[i]\)，那么后面的子串的排名也要加这么多。所以累个前缀和就好了

同时，一个前缀在它所属的后缀中的排序就是它的长度

搞定了这些，这道题就做完了，复杂度 \(O(nlog^2n)\) ，虽然没有 \(O(nlogn)\) 的优秀，但还是可以过的

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=200000+10;
char s[MAXN];
ll n,m,SA[MAXN],height[MAXN],rk[MAXN],nxt[MAXN],cnt[MAXN],val[MAXN],nt;
ll str[MAXN],sv[MAXN];
struct node{
	ll l,r;
};
node ans[MAXN];
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
#define Mid ((l+r)>>1)
#define ls rt<<1
#define rs rt<<1|1
#define lson ls,l,Mid
#define rson rs,Mid+1,r
struct Segment_Tree{
	ll Mn[MAXN<<2];
	inline void PushUp(int rt)
	{
		Mn[rt]=min(Mn[ls],Mn[rs]);
	}
	inline void Build(int rt,int l,int r)
	{
		if(l==r)Mn[rt]=height[l];
		else Build(lson),Build(rson),PushUp(rt);
	}
	inline ll Query(int rt,int l,int r,ll ps,ll k)
	{
		if(l==r)return l-(Mn[rt]>=k?1:0);
		else
		{
			if(ps>=r)
			{
				if(Mn[rs]<k)return Query(rson,ps,k);
				else return Query(lson,ps,k);
			}
			else
			{
				if(ps<=Mid||(ps>Mid&&Mn[rs]>=k))return Query(lson,ps,k);
				else return Query(rson,ps,k);
			}
		}
	}
};
Segment_Tree T;
#undef Mid
#undef ls
#undef rs
#undef lson
#undef rson
inline void GetSA()
{
	m=300;
	for(register int i=1;i<=n;++i)rk[i]=s[i];
	for(register int i=1;i<=n;++i)cnt[rk[i]]++;
	for(register int i=1;i<=m;++i)cnt[i]+=cnt[i-1];
	for(register int i=n;i>=1;--i)SA[cnt[rk[i]]--]=i;
	for(register int k=1,ps;k<=n;k<<=1)
	{
		ps=0;
		for(register int i=n-k+1;i<=n;++i)nxt[++ps]=i;
		for(register int i=1;i<=n;++i)
			if(SA[i]>k)nxt[++ps]=SA[i]-k;
		for(register int i=1;i<=m;++i)cnt[i]=0;
		for(register int i=1;i<=n;++i)cnt[rk[i]]++;
		for(register int i=1;i<=m;++i)cnt[i]+=cnt[i-1];
		for(register int i=n;i>=1;--i)SA[cnt[rk[nxt[i]]]--]=nxt[i];
		std::swap(rk,nxt);
		rk[SA[1]]=1,ps=1;
		for(register int i=2;i<=n;rk[SA[i]]=ps,++i)
			if(nxt[SA[i]]!=nxt[SA[i-1]]||nxt[SA[i]+k]!=nxt[SA[i-1]+k])ps++;
		if(ps>=n)break;
		m=ps;
	}
	for(register int i=1,j,k=0;i<=n;height[rk[i++]]=k)
		for(k=k?k-1:k,j=SA[rk[i]-1];s[i+k]==s[j+k];++k);
}
inline ll query(ll ps,ll len)
{
	ps=T.Query(1,1,n,ps,len);
	ps--;
	return (ll)str[n]-str[ps]-len+1+height[ps+1];
}
int main()
{
	scanf("%s",s+1);
	n=strlen(s+1);
	for(register int i=1;i<=n;++i)read(val[i]),sv[i]=sv[i-1]+val[i];
	GetSA();
	T.Build(1,1,n);
	for(register int i=1;i<=n;++i)str[i]=str[i-1]+n-SA[i]+1-height[i];
	for(register int i=1;i<=n;++i)
	{
		ll l=i,r=n,lt=log(r-l+1)/log(2),cl=0;
		while(l<=r)
		{
			ll mid=(l+r)>>1,sum=sv[mid]-sv[i-1],nrk=query(rk[i],mid-i+1);
			if(sum==nrk)
			{
				ans[++nt]=(node){i,mid};
				break;
			}
			if(sum>nrk)r=mid-1;
			else l=mid+1;
			cl++;
			if(cl>lt)break;
		}
	}
	write(nt,'\n');
	for(register int i=1;i<=nt;++i)write(ans[i].l,' '),write(ans[i].r,'\n');
	return 0;
}