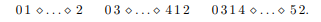BZOJ #3746: [POI2015]Czarnoksiężnicy okrągłego stołu 动态规划

　　转载请注明出处:http://www.cnblogs.com/TSHugh/p/8823423.html

　　读完题就会发现p=0、1的情况以及n=1、2的情况都可以直接判掉,而p=2的时候也可以直接构造,那么现在需要的就是当p=3且n>=3的时候的做法.
　　容易想到小数据范围下的dfs,但是这难以优化,于是去思考dp的做法.我的思路一开始是dp弧,后来发现可以直接dp两个链,但是复杂度太大,并不比dfs优秀多少.去看题解,只有Claris写了题解,他是这样写的:

p=3时不考虑1的座位进行DP
可以发现对于i+1的位置安排，我们只关心i-2,i-1,i的相对顺序以及它们的相邻、边界情况
所以设f[i][j][S1][S2]表示已经安排了前i个人的座位，i-2,i-1,i的顺序为j，是否有人在两端点为S1，是否有人相邻为S2的方案数 
答案最后再除以n
这样复杂度有点飞…

　　这并没有使我满意,因为我感觉这在时间、空间、代码各方面的复杂度都是不优秀的.
　　此时我看到了金策的700+ms做法,而且代码也并不长,这让我意识到此题有更加优秀的做法,于是在搜寻标程失败后去poi官网get了一发题解,然后利用google翻译了一发,得到了一个神奇的做法.
　　首先,题解里说了一句话,这题实际上是在数哈密顿回路,我思考了一下,好像是这样的……然而,这题的解法和哈密顿回路并没有什么卵关系……
　　转化一下问题:

I.把所有编号i变为n-i.
II.把环拆开,把原问题变成——求一段序列满足题目限制,且开头一定为0,结尾一定为1/2/3.

　　这样的话,再对三种结尾判断一下取舍,就能得到最终答案了.
　　对于现在的问题可以设计dp状态(好神奇的状态啊……):

f[i]:对于一段序列,开头为i,结尾为i+1,且序列中的数字均属于[i,n),此序列满足题目限制的方案数.
g[i]:对于一段序列,开头为i+1,结尾为i,且序列中的数字均属于[i,n),此序列满足题目限制的方案数.

　　先看dp的转移(好厉害的转移啊……):

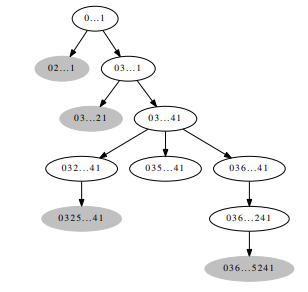
先贴一张图(来自波兰题解):

你看这张图,你就会懂得求解方法了,于是得到了一个递推式:f[i]=g[i+1]+g[i+2]+g[i+4]+g[i+5].
同理,也可以得到:g[i]=f[i+1]+f[i+2]+f[i+4]+f[i+5].
但是,上述方法似乎只适用于i<=n-8,所以,对于i>=n-7,我们就可以直接dfs处理了.
(注意判断额外限制条件)

　　假设三种结尾的方案数分别为ans1、ans2、ans3.
　　既然知道了dp的转移,那么怎么算三种ans呢?
　　沿用刚才转移的思路,可以得到(图仍然来自波兰题解):

ans1=f[0];(显然)

ans2=f[1]+f[3]+f[4];(原因见上图)

ans3=f[2]+f[4]+f[5]+g[3]+g[4];(原因见上图)
(注意判断额外限制条件)

　　所以对于p=3且n>=3的时候,判断一下,若n<=7,直接dfs,否则使用上述方法.
　　至此,这道题就解决了,时间复杂度为O(n),实现见代码:

#include <cstdio>
#include <cstring>
#include <algorithm>
char xB[(<<)+],*xS=xB,*xT=xB;
#define gtc (xS==xT&&(xT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xT)?0:*xS++)
inline void read(int &x){
  register char ch=gtc;
  for(x=;ch<''||ch>'';ch=gtc);
  for(;ch>=''&&ch<='';x=(x<<)+(x<<)+ch-'',ch=gtc);
}
const int N=;
const int Inf=0x3f3f3f3f;
const int P=;
int n,k,p,f[N],g[N];
bool NO[N][],die[N],vf[N],vg[N];
#define no(a,b) (NO[a][(b)+3])
#define ok(a,b) (!no(a,(b)-(a)))
inline int work(){
  int i,x,y,ans=;
  for(i=;i<=k;++i){
    read(x),read(y);
    if(std::abs(x-y)<=)no(x,y-x)=true;
  }
  for(i=;i<=n;++i)
    if(i&)f[(i+)>>]=i;
    else f[n-(i>>)+]=i;
  f[]=f[n],f[n+]=f[];
  ++ans;
  for(i=;i<=n;++i)
    if(no(f[i],f[i+]-f[i])){
      --ans;break;
    }
  ++ans;
  for(i=;i<=n;++i)
    if(no(f[i],f[i-]-f[i])){
      --ans;break;
    }
  printf("%d\n",ans);
  return ;
}
inline int dfs(int pos,int last,int k,int t,int len){
  if(pos==len)return std::abs(t-last)<=&&ok(last,t);
  int i,ret=;
  for(i=std::max(last-,k+);i<=last+&&i<n;++i)
    if((!die[i])&&ok(last,i)){
      die[i]=true;
      ret+=dfs(pos+,i,k,t,len);
      die[i]=false;
    }
  return ret;
}
inline int D(int s,int k,int t){
  die[s]=die[t]=true;
  int ret=dfs(,s,k,t,n-k);
  die[s]=die[t]=false;
  return ret;
}
inline int F(int x);
inline int G(int x);
inline int F(int x){
  if(vf[x])return f[x];
  vf[x]=true;
  if(n-x<=)return f[x]=D(x,x,x+);
  int ret=;
  if(ok(+x,+x))ret=(ret+G(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x))ret=(ret+G(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x))ret=(ret+G(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x))ret=(ret+G(+x))%P;
  return f[x]=ret;
}
inline int G(int x){
  if(vg[x])return g[x];
  vg[x]=true;
  if(n-x<=)return g[x]=D(x+,x,x);
  int ret=;
  if(ok(+x,+x))ret=(ret+F(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x))ret=(ret+F(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x))ret=(ret+F(+x))%P;
  if(ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x)&&ok(+x,+x))ret=(ret+F(+x))%P;
  return g[x]=ret;
}
inline int Work(){
  int i,x,y,d=,ans=;
  for(i=;i<=k;++i){
    read(x),read(y);
    x=n-x,y=n-y;
    if(std::abs(x-y)<=)no(x,y-x)=true;
  }
  if(n<=){
    if(ok(,))ans=(ans+D(,,))%P;
    if(ok(,))ans=(ans+D(,,))%P;
    if(n>=&&ok(,))ans=(ans+D(,,))%P;
    printf("%d\n",ans);
    return ;
  }
  for(i=n-d;i>d;i-=d)G(i),F(i);/*为了防止爆栈和MLE*/
  if(ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+F())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+G())%P;
  if(ok(,)&&ok(,)&&ok(,)&&ok(,)&&ok(,))ans=(ans+G())%P;
  printf("%d\n",ans);
  return ;
}
int main(){
  //freopen("cza.in","r",stdin);
  //freopen("cza.out","w",stdout);
  read(n),read(k),read(p);
  if(n==)return puts(""),;
  if(p==)return puts(""),;
  if(n==)return puts(k?"":""),;
  if(p==)return puts(""),;
  if(p==)return work(),;
  return Work(),;
}

Kod