【学习笔记】ac自动机&fail树

• 定义

  • 解决文本串和多个模式串匹配的问题；
  • 本质是由多个模式串形成的一个字典树，由tie的意义知道：trie上的每一个节点都是一个模式串的前缀；
  • 在trie上加入fail边，一个节点fail边指向这个节点所代表的前缀的最长后缀节点（除开自身的后缀）；
  • 也就是说如果x->y，那么y所代表的串是x所代表的串在trie上出现过的最大后缀；

• 例子

  • （黑边为trie，红边为fail）
  • 以"hers","she","his","i"为例：
  • 
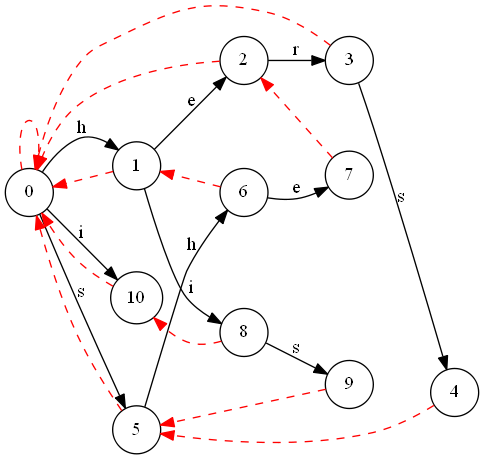
  • 原谅我的画图水平。。。如果有精通graphViz的求指点

• 构造算法

  • 离线算法，先对所有模式串建出trie，同时可以用cnt表示一个节点的有模式串的个数；
  • 规定根节点为0，fl[0] = 0，0的直接儿子的fl[v]=0；
  • 一个节点的后缀可以由它trie树上的父亲转移而来，所以按照深度bfs；
  • 假设u->v之间的边为c；
  • 所以只需要沿着fl[u]，fl[fl[u]],...，一直往上跳，找到第一个有c边的u',那么v'就是v的fl；
  • 实际实现中可以将$ch[u][i]==0$补成$fl[u]$，避免暴力往上跳;

  •  int n,len,ch[N][],sz,cnt[N],fl[N];
     char s[N];
     queue<int>q;
     void ins(){
         int u=;
         for(int i=,c;i<len;i++){
             c=s[i]-'a';
             if(!ch[u][c])ch[u][c]=++sz;
             u=ch[u][c];
         }
         cnt[u]++;
     }
     void get_fl(){
         fl[]=;
         for(int i=;i<;i++)if(ch[][i]){
             fl[ch[][i]]=;
             q.push(ch[][i]);
         }
         while(!q.empty()){
             int u=q.front();q.pop();
             for(int i=;i<;i++){
                 int&v = ch[u][i];
                 if(!v){v=ch[fl[u]][i];continue;}
                 fl[v]=ch[fl[u]][i];
                 q.push(v);
             }
         }
     }

• 性质

  • 1.匹配

  • 文本串和模式串的匹配只需不断$u=ch[u][s[i]-'a']$即可；
  • 如果匹配到自动机的一个点，那么意味着沿着fail边走到的点都被匹配了；

  • 2.fail树

  • 由于一个点的fail指针唯一，且所有点的fail都和0连通，所以fail边形成了一个数的结构；
  • 
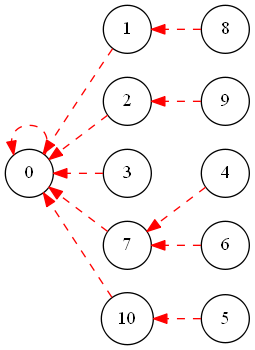
  • 沿着u的fail祖先往上走会找到u节点的所有后缀节点；
  • 对于字符串s，在自动机里匹配到的所有节点的所有fail祖先就表示s的所有子串；

• 习题

• 1.bzoj3172[Tjoi2013]单词
• ac自动机模板，由于trie树上面只存储了前缀，子串的出现次数要按照深度从大到小对每个点向fail指针累加cnt;

   #include<cstdio>
   #include<iostream>
   #include<algorithm>
   #include<cstring>
   #include<queue>
   #include<cmath>
   #include<vector>
   #include<stack>
   #include<map>
   #include<set>
   #define Run(i,l,r) for(int i=l;i<=r;i++)
   #define Don(i,l,r) for(int i=l;i>=r;i--)
   #define ll long long
   #define ld long double
   #define inf 0x3f3f3f3f
   #define mk make_pair
   #define fir first
   #define sec second
   #define il inline
   #define rg register
   #define pb push_back
   using namespace std;
   const int N=;
   int n,ch[N][],sz,fl[N],sum[N],ans[N],id[N];
   char s[N];
   int q[N],t,w;
   void ins(int now){
       int l=strlen(s),u=;
       for(int i=;i<l;i++){
           int&v=ch[u][s[i]-'a'];
           if(!v)v=++sz;
           sum[u=v]++;
       }
       id[now]=u;
   }
   void solve(){
       for(int i=;i<;i++){if(ch[][i])q[++w]=ch[][i];}
       while(t<w){
           int u=q[++t];
           for(int i=;i<;i++){
               int&v=ch[u][i];
               if(!v)v=ch[fl[u]][i];
               else fl[v]=ch[fl[u]][i],q[++w]=v;
           }
       }
       for(int i=w;i;i--)sum[fl[q[i]]]+=sum[q[i]];
       for(int i=;i<=n;i++)printf("%d\n",sum[id[i]]);
   }
   int main(){
   //    freopen("bzoj3172.in","r",stdin);
   //    freopen("bzoj3172.out","w",stdout);
       scanf("%d",&n);
       for(int i=;i<=n;i++){scanf("%s",s);ins(i);}
       solve();
       return ;
   }//by tkys_Austin;

  bzoj3172

• 2.bzoj1212[Hnoi2004]L语言
• n，m都很小；$f[i]$表示前缀i是否可以被理解，$f[i]$可以从$f[j]（j<i）$转移的条件是$s[j+1]---S[i]$可以被理解，暴力判断应该会T
• 对字典建自动机，如果把文章跑一遍，可以直接用fail指针暴力往上跳就可以找到所有的可以转移的j； 

   #include<bits/stdc++.h>
   #define rg register
   #define il inline
   using namespace std;
   const int N=;
   int n,m,len,ch[N][],sz,lst[N],head,tail,q[N],dep[N],vis[N],fl[N],ans;
   bool f[N];
   char s[N];
   il char gc(){
       static char*p1,*p2,s[];
       if(p1==p2)p2=(p1=s)+fread(s,,,stdin);
       return(p1==p2)?EOF:*p1++;
   }
   il int rd(){
       int x=;char c=gc();
       while(c<''||c>'')c=gc();
       while(c>=''&&c<='')x=(x<<)+(x<<)+c-'',c=gc();
       return x;
   }
   il void gt(){
       char *p = s,c = gc();
       while(c<'a'||c>'z')c=gc();
       while(c>='a'&&c<='z')*p++ = c,c=gc();
       len = p - s;
   }
   il void ins(){
       int u=;
       for(rg int i=;i<len;i++){
           if(!ch[u][s[i]-'a'])ch[u][s[i]-'a']=++sz;
           u = ch[u][s[i]-'a'];
       }
       vis[u] = ;
   }
   void get_fl(){
       for(int i=;i<;i++)if(ch[][i]){
           q[++tail]=ch[][i];
           dep[ch[][i]]=;
       }
       while(head<tail){
           int u=q[++head];
           for(int i=;i<;i++){
               int&v=ch[u][i];
               if(!v){v=ch[fl[u]][i];continue;}
               dep[v] = dep[u] + ;
               fl[v] = ch[fl[u]][i];
               if(vis[fl[v]])lst[v]=fl[v];else lst[v]=lst[fl[v]];
               q[++tail]=v;
           }
       }
   }
   il bool find(int x,int pos){
       if(!x)return false;
       if(vis[x]&&f[pos-dep[x]])return true;
       return find(lst[x],pos);
   }
   void query(){
       f[] = true;
       for(rg int i=,u=;i<=len;i++){
           u = ch[u][s[i-]-'a'];
           f[i] = find(u,i);
           if(f[i]) ans = i;
       }
   }
   int main(){
       freopen("bzoj1212.in","r",stdin);
       freopen("bzoj1212.out","w",stdout);
       n=rd();m=rd();
       for(rg int i=;i<=n;i++)gt(),ins();
       get_fl();
       for(rg int i=;i<=m;i++){
           gt();
           memset(f,,sizeof(bool)*(len+));
           ans = ;
           query();
           printf("%d\n",ans);
       }
       return ;
   }

  bzoj1212

• 3.bzoj1030[Jsoi2007]文本生成器   (bzoj3530类似)
• 如果直接问一个已知的文本是否含有给出单词就是模板题了；
• 同样我们只关心给出的模板串，对模板建自动机做dp
• $dp[i][j]$表示生成了前$i$位，当前匹配状态为自动机的$j$号节点；
• 新开一个节点统计答案，每次都自乘*26；
• 枚举下一个字符k,考虑转移到ch[j][k] , 注意如果ch[j][k]是一个已经匹配了单词的节点就直接转移到统计答案的节点
• 初始f[0][0]=1;
• O(N*Len)某些情况下可写成矩阵乘法转移
• 我写的时候犯了点错：

• 但是ac自动机的匹配算法中，注意所有匹配走过路径的节点并不是所有的单词节点，因为可能会有中间匹配点可以按照失配边走到有串的节点，所以代码里vis要沿fail向下传递；

   #include<bits/stdc++.h>
   #define rg register
   #define il inline
   using namespace std;
   const int N=,M=,mod=;
   int n,m,ch[N*M][],f[M][N*M],vis[N*M],fl[N*M],head,tail,q[N*M],sz;
   char s[M];
   il void ins(){
       int l = strlen(s) , u=;
       for(rg int i=;i<l;i++){
           int& v = ch[u][s[i]-'A'];
           if(!v)v = ++sz;
           u = v;
       }
       vis[u]=;
   }
   void get_fl(){
       for(int i=;i<;i++)if(ch[][i])q[++tail]=ch[][i];
       while(head<tail){
           int u = q[++head];
           for(rg int i=;i<;i++){
               int& v=ch[u][i];
               if(!v){v=ch[fl[u]][i];continue;}
               fl[v]=ch[fl[u]][i];
               q[++tail]=v;
           }
       }
       for(rg int i=;i<=tail;i++)vis[q[i]] |= vis[fl[q[i]]];
   }
   il void upd(int&x,int y){x+=y;if(x>=mod)x-=mod;}
   int main(){
       freopen("bzoj1030.in","r",stdin);
       freopen("bzoj1030.out","w",stdout);
       scanf("%d%d",&n,&m);
       for(rg int i=;i<=n;i++){scanf("%s",s);ins();}
       get_fl();
       f[][]=;
       for(rg int i=;i<m;i++){
           for(rg int j=;j<=sz;j++){
               for(rg int k=;k<;k++){
                   if(vis[ch[j][k]])upd(f[i+][sz+],f[i][j]);
                   else upd(f[i+][ch[j][k]],f[i][j]);
               }
           }
           upd(f[i+][sz+],f[i][sz+]*%mod);
       }
       cout<<f[m][sz+]<<endl;
       return ;
   }

  bzoj1030

• 4.bzoj1444[Jsoi2009]有趣的游戏
• https://www.cnblogs.com/clrs97/p/4987277.html     ORZ
• 不妨吧trie树上的有单词的节点叫做关键点，其他是非关键点；
• 这题有意思的地方在于只能在关键点停下来；
• 直接的想法是：用自动机建立概率方程，每个点的概率等于所有指向它的节点贡献之和，同时关键点不让转移(即不贡献出边)；
• 然而这样也没有常数项。。。。。。。解出来都是0？？？！接下来的操作比较神奇：
• 把0号点的方程(也有人说随意那个)用所有关键点概率之和==0替换再高斯消元即可,小心会输出-0.00所以要特判一下；
• （如果有更好的理解希望指点，感激不尽）

   #include<bits/stdc++.h>
   #define ld double
   #define rg register
   #define il inline
   using namespace std;
   const int N=;
   int n,l,m,sz,id[N],vis[N],fl[N],q[N],t,w,ch[N][],px[N],py[N];
   ld p[N],a[N][N];
   char s[N];
   void get_fl(){
       for(int i=;i<m;i++)if(ch[][i])q[++w]=ch[][i];
       while(t<w){
           int u = q[++t];
           for(int i=;i<m;i++){
               int&v = ch[u][i];
               if(!v){v=ch[fl[u]][i];continue;}
               fl[v]=ch[fl[u]][i];
               q[++w]=v;
           }
       }
       a[][sz+]=;
       for(int i=;i<=sz;i++){
           if(i)a[i][i]=;
           if(vis[i]){a[][i]=;continue;}
           for(int j=;j<m;j++)if(px[j]){
               int v = ch[i][j];
               if(v)a[v][i] -= p[j];
           }
       }
   }
   void gauss(){
       for(rg int i=;i<=sz;i++){
           int pos=i;
           for(rg int j=i+;j<=sz;j++)if(fabs(a[j][i])>fabs(a[pos][i]))pos=j;
           if(pos!=i)for(rg int j=i;j<=sz+;j++)swap(a[i][j],a[pos][j]);
           for(rg int j=i+;j<=sz;j++){
               ld tmp = a[j][i] / a[i][i];
               for(rg int k=i;k<=sz+;k++)a[j][k] -= tmp * a[i][k];
           }
       }
       for(rg int i=sz;~i;i--){
           for(rg int j=i+;j<=sz;j++)a[i][sz+] -= a[j][sz+] * a[i][j];
           a[i][sz+] /= a[i][i];
       }
   }
   int main(){
       freopen("bzoj1444.in","r",stdin);
       freopen("bzoj1444.out","w",stdout);
       scanf("%d%d%d",&n,&l,&m);
       for(int i=;i<m;i++){
           scanf("%d%d",&px[i],&py[i]);
           p[i] = 1.0 * px[i] / py[i];
       }
       for(int i=;i<=n;i++){
           scanf("%s",s);
           int u=;
           for(int j=;j<l;j++){
               if(!ch[u][s[j]-'A'])ch[u][s[j]-'A']=++sz;
               u = ch[u][s[j]-'A'];
           }
           id[i] = u; vis[u] = ;
       }
       get_fl();
       gauss();
       for(int i=;i<=n;i++){
           ld x = fabs(a[id[i]][sz+]);
       //    x = fabs(-0.00);
           if(x>)printf("%.2lf\n",x);
           else puts("0.00");
       }
       return ;
   }

  bzoj1444

• 5.bzoj2434[Noi2011]阿狸的打字机
• 模拟操作建自动机，考虑现在有一颗trie树和fail树
• x在y里面出现的次数 == 在trie树上y的所有祖先 在x在fail树上的子树里的有多少个
• 维护这可以直接在trie上dfs，树状数组区间修改维护当前点到trie的根再fail树的dfs序，查询子树信息；
• 或者直接对trie树链剖建主席树，权值是fail树的dfs序；

   #include<bits/stdc++.h>
   #define rg register
   #define il inline
   #define pb push_back
   using namespace std;
   const int N=,M=;
   int n,m,ch[N][],fa[N],tot,cnt,que[N],head,tail,fl[N],a[N];
   int id[N],pos[N],st[N],ed[N],sum[N*M],sz,tp[N],idx,son[N],size[N],rt[N],ls[N*M],rs[N*M];
   vector<int>g[N];
   char s[N];
   il char gc(){
       static char *p1,*p2,s[];
       if(p1==p2)p2=(p1=s)+fread(s,,,stdin);
       return(p1==p2)?EOF:*p1++;
   }
   il int rd(){
       int x=; char c=gc();
       while(c<''||c>'')c=gc();
       while(c>=''&&c<='')x=(x<<)+(x<<)+c-'',c=gc();
       return x;
   }
   il int gt(){
       char*p = s , c = gc();
       while(!isalpha(c))c=gc();
       while(isalpha(c))*p++=c,c=gc();
       return p - s;
   }
   void get_fl(){
       for(int i=;i<;i++)if(ch[][i]){
           que[++tail]=ch[][i];
           g[].pb(ch[][i]);
       }
       while(head<tail){
           int u=que[++head];
           for(int i=;i<;i++){
               int& v=ch[u][i];
               if(!v){v=ch[fl[u]][i];continue;}
               fl[v]=ch[fl[u]][i];
               g[fl[v]].pb(v);
               que[++tail] = v;
           }
       }
   }
   void dfs1(int u){
       size[u]=;son[u]=;
       for(int i=;i<;i++){
           int v = ch[u][i];
           if(!v||v==fa[u])continue;
           dfs1(v);
           size[u]+=size[v];
           if(!son[u]||size[v]>size[son[u]])son[u]=v;
       }
   }
   void dfs2(int u,int top){
       a[pos[u]=++idx]=u;
       tp[u]=top;
       if(son[u])dfs2(son[u],top);
       for(int i=;i<;i++){
           int v=ch[u][i];
           if(!v||v==fa[u]||v==son[u])continue;
           dfs2(v,v);
       }
   }
   void dfs(int u){
       st[u] = ++idx;
       for(int i=;i<(int)g[u].size();i++){
           int v = g[u][i];
           dfs(v);
       }
       ed[u] = idx;
   }
   il void ins(int&k,int lst,int l,int r,int x,int y){
       sum[k=++sz]=sum[lst]+y;
       ls[k]=ls[lst];rs[k]=rs[lst];
       if(l==r)return ;
       int mid=(l+r)>>;
       if(x<=mid)ins(ls[k],ls[lst],l,mid,x,y);
       else ins(rs[k],rs[lst],mid+,r,x,y);
   }
   il int query(int k,int lst,int l,int r,int x,int y){
       if(l==x&&r==y)return sum[k]-sum[lst];
       else{
           int mid=(l+r)>>;
           if(y<=mid)return query(ls[k],ls[lst],l,mid,x,y);
           else if(x>mid)return query(rs[k],rs[lst],mid+,r,x,y);
           else return query(ls[k],ls[lst],l,mid,x,mid)+query(rs[k],rs[lst],mid+,r,mid+,y);
       }
   }
   il int Query(int x,int y){
       int re=;
       while(~x){
           re += query(rt[pos[x]],rt[pos[tp[x]]-],,cnt,st[y],ed[y]);
           x = fa[tp[x]];
       }
       return re;
   }
   int main(){
       freopen("bzoj2434.in","r",stdin);
       freopen("bzoj2434.out","w",stdout);
       n=gt();
       int u = ;
       for(rg int i=;i<n;i++){
           if(s[i]=='B')u = fa[u];
           else if(s[i]=='P')id[++tot] = u;
           else {
               if(!ch[u][s[i]-'a'])ch[u][s[i]-'a']=++cnt;
               fa[ch[u][s[i]-'a']] = u;
               u = ch[u][s[i]-'a'];
           }
       }
       fa[]=-;
       dfs1();
       dfs2(,);
       get_fl();
       idx=;dfs();
       cnt++;
       for(rg int i=;i<=cnt;i++){ins(rt[i],rt[i-],,cnt,st[a[i]],);}
       m = rd();
       for(rg int i=,x,y;i<=m;i++){
           x = rd() , y=rd();
           int ans = Query(id[y],id[x]);
           printf("%d\n",ans);
       }
       return ;
   }

  bzoj2434