Codeforces Round #263 (Div. 1)

B 树形dp

组合的思想。

Z队长的思路。

dp[i][1]表示以i为跟结点的子树向上贡献1个的方案，dp[i][0]表示以i为跟结点的子树向上贡献0个的方案.

如果当前为叶子节点，dp[i][0] = 1，（颜色为1，可以断开与父节点的连接，颜色为0，不断开，方案恒为1），dp[i][1] = co[i]（i节点的颜色）。

非叶子节点：将所有孩子节点的dp[child][0]乘起来为sum，孩子贡献为0的总方案。

当前颜色为0时， dp[i][1] += sum/dp[child][0]*dp[child][1],（选当前孩子贡献的1） ，

dp[i][0] = sum+dp[i][1](将i与其父亲断开)。

当颜色为1时，  dp[i][1] （需儿子们贡献为0）= dp[i][0](需与父亲断开) = sum.

中间除法取模需要用到逆元。 (s/y)%mod = (s*y^mod-2)%mod;

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 100010
 #define LL long long
 #define INF 0xfffffff
 #define mod 1000000007
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 vector<int>ch[N];
 int dp[N][];
 int co[N];
 LL q_mod(LL a,LL b)
 {
     LL d,t;
     d = ,t=a;
     while(b)
     {
         if(b&) d = (d*t)%mod;
         b/=;
         t = (t*t)%mod;
     }
     return d;
 }
 LL cal(LL s,LL y,LL x)
 {
     s = (s*x)%mod;
     return (s*q_mod(y,mod-))%mod;
 }
 void dfs(int u,int pre)
 {
     int i;
     LL s0=;
     int flag = ;
     for(i =  ; i < ch[u].size() ;i++)
     {
         int v = ch[u][i];
         if(v==pre) continue;
         flag = ;
         dfs(v,u);
         s0 = (s0*dp[v][])%mod;
     }
     if(!flag)
     {
         dp[u][] = ;
         dp[u][] = co[u];
         return ;
     }
     if(co[u]==)
     {
         dp[u][] = s0;
         dp[u][] = ;
         for(i =  ;i < ch[u].size() ; i++)
         {
             int v = ch[u][i];
             if(v==pre) continue;
             if(!dp[v][]) continue;
             dp[u][] = (dp[u][]+cal(s0,dp[v][],dp[v][]))%mod;
         }
         dp[u][] = (dp[u][]+dp[u][])%mod;
     }
     else
     {
         dp[u][] = s0;
         dp[u][] = s0;
     }
 }
 int main()
 {
     int n,i;
     cin>>n;
     for(i =  ; i < n-; i++)
     {
         int u;
         scanf("%d",&u);
         ch[u].push_back(i+);
         ch[i+].push_back(u);
     }
     for(i =  ; i < n; i++)
     scanf("%d",&co[i]);
     dfs(,-);
     cout<<dp[][]<<endl;
     return ;
 }

C 标记数组开始和尾部 线段树维护。

因为有翻转操作，当前数组的开始与结尾不确定，用两个变量标记。

线段树节点表示以它为右端点的线段   比如 0-1-2-3-4-5-6  分别用1 2 3 4 5 6表示它左边那条线段。

如果旋转位置大于当前线段长度的一半，先把此线段翻转，再翻转相对的较短一段。

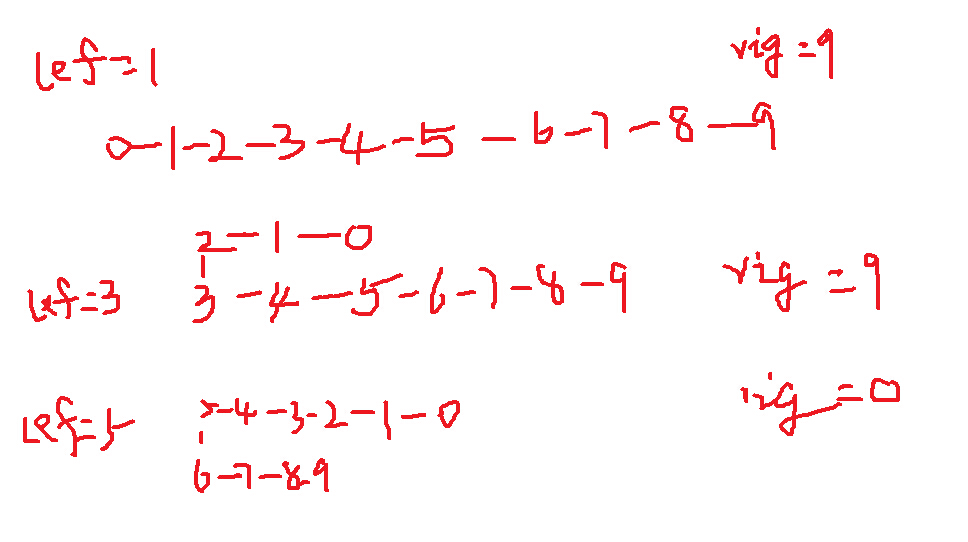
 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 100000
 #define LL long long
 #define INF 0xfffffff
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 int s[N<<];
 int a[N];
 void up(int w)
 {
     s[w] = s[w<<]+s[w<<|];
 }
 void build(int l,int r,int w)
 {
     if(l==r)
     {
         s[w] = a[l] = ;
         return ;
     }
     int m = (l+r)>>;
     build(l,m,w<<);
     build(m+,r,w<<|);
     up(w);
 }
 void update(int p,int d,int l,int r,int w)
 {
     if(l==r)
     {
         s[w]+=d;
         a[l] = s[w];
         return ;
     }
     int m = (l+r)>>;
     if(p<=m) update(p,d,l,m,w<<);
     else update(p,d,m+,r,w<<|);
     up(w);
 }
 int query(int a,int b,int l,int r,int w)
 {
     if(a<=l&&b>=r)
     {
         return s[w];
     }
     int m = (l+r)>>;
     int res = ;
     if(a<=m) res+=query(a,b,l,m,w<<);
     if(b>m) res+=query(a,b,m+,r,w<<|);
     return res;
 }
 int main()
 {
     int n,m,i,j;
     cin>>n>>m;
     build(,n,);
     int lef=,rig=n;
     while(m--)
     {
         int x,y,z;
         scanf("%d%d",&x,&y);
         if(x==)
         {
             int mid = (abs(rig-lef)+)>>;
             //cout<<mid<<" .."<<rig<<" "<<lef<<endl;
             if(y>mid)
             {
                 swap(lef,rig);
                 y = abs(rig-lef)+-y;
             }
             //cout<<y<<".."<<endl;
             int st,en;
             if(lef<rig)
             {
                 st = lef+y-;
                 j = st+;
                 for(i = st ; i >= lef ; i--)
                 {
                     update(j,a[i],,n,);
                     j++;
                 }
                 lef = st+;
             }
             else
             {
                 st = lef-y+;
                 j = st-;
                 for(i = st ;i <= lef ;i++)
                 {
                     update(j,a[i],,n,);
                     j--;
                 }
                 lef = st-;
             }
         }
         else
         {
             scanf("%d",&z);
             y++;
             int ll,rr;
             if(lef>rig)
             {
                 ll = lef-z+;
                 rr = lef-y+;
             }
             else
             {
                 ll = lef+y-;
                 rr = lef+z-;
             }
             cout<<query(ll,rr,,n,)<<endl;
         }
     }
     return ;
 }