【数据压缩】LZ78算法原理及实现

在提出基于滑动窗口的LZ77算法后，两位大神Jacob Ziv与Abraham Lempel于1978年在发表的论文 [1]中提出了LZ78算法；与LZ77算法不同的是LZ78算法使用动态树状词典维护历史字符串。

【数据压缩】LZ77算法原理及实现

【数据压缩】LZ78算法原理及实现

1. 原理

压缩

LZ78算法的压缩过程非常简单。在压缩时维护一个动态词典Dictionary，其包括了历史字符串的index与内容；压缩情况分为三种：

1. 若当前字符c未出现在词典中，则编码为(0, c)；
2. 若当前字符c出现在词典中，则与词典做最长匹配，然后编码为(prefixIndex,lastChar)，其中，prefixIndex为最长匹配的前缀字符串，lastChar为最长匹配后的第一个字符；
3. 为对最后一个字符的特殊处理，编码为(prefixIndex,)。

如果对于上述压缩的过程稍感费解，下面给出三个例子。例子一，对于字符串“ABBCBCABABCAABCAAB”压缩编码过程如下：

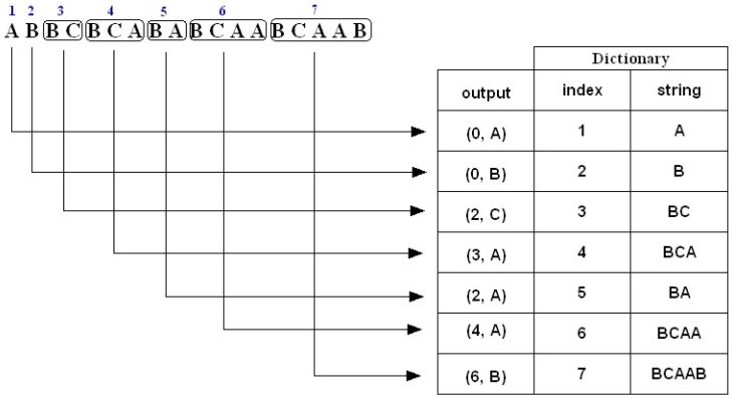
1. A is not in the Dictionary; insert it
2. B is not in the Dictionary; insert it
3. B is in the Dictionary.
    BC is not in the Dictionary; insert it.
4. B is in the Dictionary.
    BC is in the Dictionary.
    BCA is not in the Dictionary; insert it.
5. B is in the Dictionary.
    BA is not in the Dictionary; insert it.
6. B is in the Dictionary.
    BC is in the Dictionary.
    BCA is in the Dictionary.
    BCAA is not in the Dictionary; insert it.
7. B is in the Dictionary.
    BC is in the Dictionary.
    BCA is in the Dictionary.
    BCAA is in the Dictionary.
    BCAAB is not in the Dictionary; insert it.

例子二，对于字符串“BABAABRRRA”压缩编码过程如下：

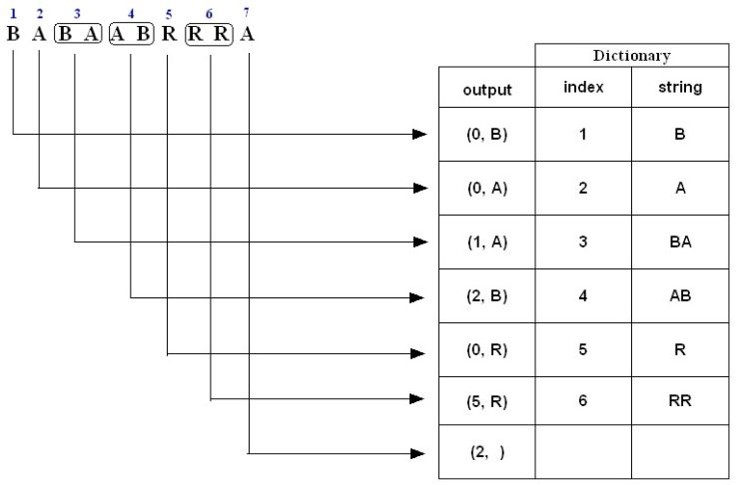
1.  B is not in the Dictionary; insert it
2.  A is not in the Dictionary; insert it
3.  B is in the Dictionary.
     BA is not in the Dictionary; insert it.
4.  A is in the Dictionary.
     AB is not in the Dictionary; insert it.
5.  R is not in the Dictionary; insert it.
6.  R is in the Dictionary.
     RR is not in the Dictionary; insert it.
7.  A is in the Dictionary and it is the last input character; output a pair
      containing its index: (2, )

例子三，对于字符串“AAAAAAAAA”压缩编码过程如下：

1.  A is not in the Dictionary; insert it
2.  A is in the Dictionary
     AA is not in the Dictionary; insert it
3.  A is in the Dictionary.
     AA is in the Dictionary.
     AAA is not in the Dictionary; insert it.
4.  A is in the Dictionary.
     AA is in the Dictionary.
     AAA is in the Dictionary and it is the last pattern; output a pair containing its index: (3,  )

解压缩

解压缩能更根据压缩编码恢复出（压缩时的）动态词典，然后根据index拼接成解码后的字符串。为了便于理解，我们拿上述例子一中的压缩编码序列(0, A) (0, B) (2, C) (3, A) (2, A) (4, A) (6, B)来分解解压缩步骤，如下图所示：

前后拼接后，解压缩出来的字符串为“ABBCBCABABCAABCAAB”。

LZ系列压缩算法

LZ系列压缩算法均为LZ77与LZ78的变种，在此基础上做了优化。

• LZ77：LZSS、LZR、LZB、LZH；
• LZ78：LZW、LZC、LZT、LZMW、LZJ、LZFG。

其中，LZSS与LZW为这两大阵容里名气最响亮的算法。LZSS是由Storer与Szymanski [2]改进了LZ77：增加最小匹配长度的限制，当最长匹配的长度小于该限制时，则不压缩输出，但仍然滑动窗口右移一个字符。Google开源的Snappy压缩算法库大体遵循LZSS的编码方案，在其基础上做了一些工程上的优化。

2. 实现

Python 3.5实现LZ78算法：

# -*- coding: utf-8 -*-
# A simplified implementation of LZ78 algorithm
# @Time    : 2017/1/13
# @Author  : rain

def compress(message):
    tree_dict, m_len, i = {}, len(message), 0
    while i < m_len:
        # case I
        if message[i] not in tree_dict.keys():
            yield (0, message[i])
            tree_dict[message[i]] = len(tree_dict) + 1
            i += 1
        # case III
        elif i == m_len - 1:
            yield (tree_dict.get(message[i]), '')
            i += 1
        else:
            for j in range(i + 1, m_len):
                # case II
                if message[i:j + 1] not in tree_dict.keys():
                    yield (tree_dict.get(message[i:j]), message[j])
                    tree_dict[message[i:j + 1]] = len(tree_dict) + 1
                    i = j + 1
                    break
                # case III
                elif j == m_len - 1:
                    yield (tree_dict.get(message[i:j + 1]), '')
                    i = j + 1

def uncompress(packed):
    unpacked, tree_dict = '', {}
    for index, ch in packed:
        if index == 0:
            unpacked += ch
            tree_dict[len(tree_dict) + 1] = ch
        else:
            term = tree_dict.get(index) + ch
            unpacked += term
            tree_dict[len(tree_dict) + 1] = term
    return unpacked

if __name__ == '__main__':
    messages = ['ABBCBCABABCAABCAAB', 'BABAABRRRA', 'AAAAAAAAA']
    for m in messages:
        pack = compress(m)
        unpack = uncompress(pack)
        print(unpack == m)

3. 参考资料

[1] Ziv, Jacob, and Abraham Lempel. "Compression of individual sequences via variable-rate coding." IEEE transactions on Information Theory 24.5 (1978): 530-536.

[2] Storer, James A., and Thomas G. Szymanski. "Data compression via textual substitution." Journal of the ACM (JACM) 29.4 (1982): 928-951.

[3] Welch, T. A. "A Technique for High-Performance Data Compression." Computer 17.17(1984):8-19.

[4] Jauhar Ali, Unit31_LZ78.ppt.

[5] guyb, 15-853:Algorithms in the Real World - Data Compression III.