考试总结T2（接上次整的T1）

首先说一句,树的每个元素的名称的问题,(那个叫jie点的东西)

具体是节点还是结点...baidu百科写的是结点...

本文章将不考虑到底这俩字怎么写...所以两种都可能出现

T2描述：

扶苏翻遍了歌单却没有找到一首歌能做这个题的题目背景，于是放上了扶苏最喜欢的一首《不老梦》.

与Day1的第二题一样，今天的第二题依然是一道树论题.

我们定义一棵\(n\)个节点的树为一个有\(n\)个节点和\(n-1\)条边的无向连通图.

如果我们定义\(u\)是一颗树\(T\)的根，那么任意一个节点\(v\)到根的路径就是从\(v\)出发到达点\(u\)的简单路径上所经过的点的点集。可以证明这样的简单路径有且仅有一条

定义一个节点\(x\)是节点\(y\)的孩子，当且仅当\(x\)和\(y\)之间有边相连且\(x\)不在\(y\)到根的路径中。如果\(x\)是\(y\)的孩子，那么定义\(y\)是\(x\)的家长节点.

如果我是_rqy那种毒瘤神仙的话，可能会问你每个节点的孩子数不超过\(k\)的\(n\)个节点的带标号无根树一共有多少个，可惜这个问题我也不会，所以我不会问你这么毒瘤的问题.

扶苏从一颗\(n\)个节点的树的1号节点出发，沿着树上的边行走。当然我们约定1号节点是这棵树的根。他所行走的规定是：当扶苏在点 \(u\)时，扶苏要么在\(u\)的孩子中选择一个没有到达过得点\(v\)并行走到\(v\)，要么选择回到\(u\)的家长节点.

现在给每个节点一个权值\(w\)，其中i 号节点的权值为\(w_i\)。扶苏有一些石子，他想给这棵树上的某一个节点放上石子。我们规定扶苏能在节点\(u\)放上石子当且仅当满足如下条件：

1、扶苏当前在节点\(u\)

2、对于\(u\)的所有孩子节点\(v\)，节点\(v\)被放上了\(w_v\) 颗石子。

但是，扶苏在任意时刻都可以取回任意节点的石子。

现在，扶苏想问问你对于每个节点，如果他想在i 号节点上放\(w_i\)颗石子，那么他一开始需要准备多少石子.

有人说T3比T2简单,然而我在考场上对于T2更有思路...

今天大佬在讲题时跟我的思路大致一致(woc大致一致!!!!)

分析思路:

由题可知,要拿到整体最优需要考虑前面的石子如何才能充分利用

我们知道前面节点的石子能够利用的条件是当前处理子节点的几个儿子节点已满并且孙子节点非空,再且就是当其同辈节点已经填上石子的情况下,将其孩子节点进行"剥削",将其石子取走,

现在难免要面对这么一个问题:

在处理某一个节点(就是同辈节点)的最小花费时,如何安排顺序才能致使结果最优呢?

现在考虑一层有\(n\)个节点,其中该层节点本身需要的石子数先不考虑,只考虑其

因为现在我们考虑每个节点处理的顺序的原因是要考虑对其子节点所含石子的利用,

就是要考虑哪个节点的子节点所含石子在填满(满足填该节点本身)并且该节点已经填了石子时,其子节点的石子可以拿出来用,

那么如果当前节点的子节点石子较多，在把此节点的石子填上以后，可重复利用的石子也较多

举个栗子啦....

如图：



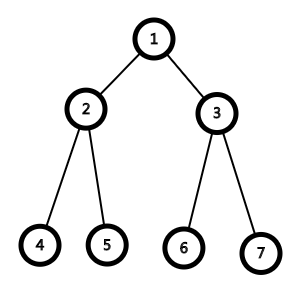
现在假如4 5节点需要8个石子，6 7节点需要90个石子，2节点需要2个石子，3节点需要10个石子,

分两种情况讨论：

1.先填2节点（意味着先填满4 5节点）

那么先取8+2个石子填满2,4,5节点,现在可以拿出2号节点的子节点中所有石子(当然2节点不能取)来填3号及其子节点,那么取下面的8个石子,现在右边需要的总共100个石子中填了8个,还需另外92个石子,只能再次造成花费,添加石子,此时显然造成了极大浪费,需要使用108个石子.

2.先填3节点

先取100个石子填3号及其子节点,辣么那么现在的花费是100,再同样将3号的子节点石子取出利用,填2号等,此时我们发现这90个剩余石子不仅能够完成填满2号及其子节点的任务,还能去填1号节点或是2,3号的兄弟节点,(仅在这棵确定的二叉树下)对于填满2,3所在层,仅需石子100枚(怎么量词突然正经?)

通过以上案例模拟易知,也可推知,在处理某层节点时,需要先处理子节点所含石子多的,

(当时考虑暴搜来着,实际就是暴搜,然而并不会处理变量关系...)

再同样的复读一遍给出公式推导与证明:

设本层有两个节点\(i\)与\(j\),设其子节点所含石子总数为\(a_i\)与\(a_j\),

其本身的花费为\(w_i\)与\(w_j\),现在令\(a_i>a_j\)

则有:

先买\(i\)的花费是\(max(w_i+a_i,w_i+w_j+a_j)\)

同理先买\(j\)的花费是\(max(w_j+a_j,w_j+w_i+a_i)\)

化简得这样两个式子:

\(w_i+max(a_i,w_j+a_j)\)

\(w_j+max(a_j,w_i+a_i)\)

展开式子:

1式有两种情况:

\(w_i+a_i\)或\(w_i+w_j+a_j\)

然而第二个铁定只有一种:

\(w_j+a_i+w_i\), 因为\(a_i\)始终大于\(a_j\)

作差一减便知,无论如何二式减一式总大于等于零,

所以无论如何选\(a_{较大的那个}\)总是最优方案,扩展一下会发现这是无论树高的统一结论,

现在剩下所要做的就是搜索!!

现在需要注意几点:

1.考虑的处理顺序序列其实是不上升序列而非递减序列,因为可以有相等的情况出现...

2.在进行深搜时,如果一个个跑一边就显得太蠢了,不如在每次递归处理子节点时将节点按此规则排序,这也是一种优化的方案, 不然会丢30分(一个点30分)

没亲测,但有效~

代码贴上(又是好神奇的二空格首行缩进,这就是强者的世界嘛?):

#include <cstdio>
#include <vector>
#include <algorithm>
const int maxn = 100010;
int n;
int MU[maxn], ans[maxn];
std::vector<int>son[maxn];
void dfs(const int u);
bool cmp(const int &_a, const int &_b);
int main() {
  freopen("yin.in", "r", stdin);
  freopen("yin.out", "w", stdout);
  scanf("%d", &n);
  for (int i = 2, x; i <= n; ++i) {
    scanf("%d", &x);
    son[x].push_back(i);
  }
  for (int i = 1; i <= n; ++i) {
    scanf("%d", MU + i);
  }
  dfs(1);
  for (int i = 1; i < n; ++i) {
    printf("%d ", ans[i]);
  }
  printf("%d\n", ans[n]);
  return 0;
}

void dfs(const int u) {
  for (auto v : son[u]) {
    dfs(v);
  }
  std::sort(son[u].begin(), son[u].end(), cmp);
  int _ret = 0;
  for (auto v : son[u]) {
    if (_ret >= ans[v]) {
      _ret -= ans[v];
    } else {
      ans[u] += ans[v] - _ret;
      _ret = ans[v] - MU[v];
    }
  }
  ans[u] += std::max(0, MU[u] - _ret);
}

inline bool cmp(const int &_a, const int &_b) {
  return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]);
}