FJUT2019暑假周赛一题解

A.排队问题*-*

题意就是有长度为L的序列，每位的取值可以是'f'或者'm'，问不包含'fff'和'fmf'的个数。

打表找规律

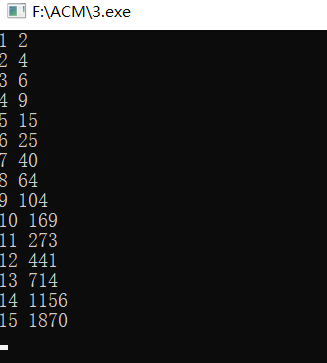
不难找出递推公式为F[n] = F[n-1] + F[n-3] + F[n-4]。

然后直接遍历就可以了...突然发现L范围很小，我写了个矩阵快速幂...

多组数据且模数不固定，矩阵快速幂即可

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;

 int n,mod;

 struct M {
     ll p[][];
     M(int num) {
         memset(p,,sizeof p);
         for (int i = ; i < ; i++) {
             p[i][i] = num;
         }
     }

     M operator * (M b) {
         M c();
         for (int i = ; i < ; i++) {
             for (int j = ; j < ; j++) {
                 c.p[i][j] = ;
                 for (int k = ; k < ; k++) {
                     c.p[i][j] = (c.p[i][j] + (p[i][k]*b.p[k][j])%mod)%mod;

                 }
             }
         }
         return c;
     }

     M operator ^ (ll k) {
         M c(),a = *this;
         while (k) {
             if (k&) {
                 c = a*c;
             }
             a = a*a;
             k >>= ;
         }
         return c;
     }

 };
 M a(),b();
 int solve() {
     M c();

     if (n == ) {
         return ;
     } else if (n <= ) {
         return a.p[-n][]%mod;
     }
     c = b^(n-);
     c = c*a;
     return c.p[][]%mod;
 }

 string s;

 void db() {
     for (int i = ; i <= ; i++) {
         int p = pow(2.0,i),tot = ,cnt = ;
         for (int j = ; j < p; j++) {
             int tmp = ;
             s = "";
             for (int k = ; k <= i; k++) {
                 if (tmp&j) {
                     s += 'f';
                 } else {
                     s += 'm';
                 }
                 tmp <<= ;
             }
             for (int k = ; k < int(s.size())-; k++) {
                 if (s[k] =='f' && s[k+] == 'm' && s[k+] == 'f') {
                     cnt++;
                     break;
                 } else if (s[k] =='f' && s[k+] == 'f' && s[k+] == 'f') {
                     cnt++;
                     break;
                 }
             }
             tot++;
         }
         cout << i << ' ' << p-cnt << endl;
     }
 }
 /*
     f_i = f_{i-1} + f_{i-3} +f_{i-4};
     1 0 1 1
     1 0 0 0
     0 1 0 0
     0 0 1 0
 */
 int main() {
     ios_base::sync_with_stdio();
     cin.tie();
     db();

     a.p[][] = ;
     a.p[][] = ;
     a.p[][] = ;
     a.p[][] = ;
     b.p[][] = ;
     b.p[][] = ;
     b.p[][] = ;
     b.p[][] = ;
     b.p[][] = ;
     b.p[][] = ;
     while (cin >> n >> mod) {
         cout << solve() << endl;
     }
     return ;
 }

此处应有严格证明递推公式的由来，然而我不会。。。

B.就差把标程贴上去了

公式都已经放出来了

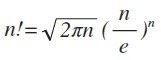
一个数的长度也就是len(x) = log(x)/log(10) + 1，这里我们取对数就可以得到len(n!) = 1/2*log10(2.0*PI*n) + n*log10(n/e)+1。

这里其实就够了，当然你可以继续化简到和我代码一样= =

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 #define pi (acos(-1))
 ll n,d;

 void solve() {
     cin >> n;
     d = (int) ((0.5*log(*pi*n) + n*log(n)-n) / log ());
     cout << d+ << endl;
 }

 int main() {
     ios_base::sync_with_stdio();
     cin.tie();
     int _;
     cin >> _;
     while (_--) {
         solve();
     }
     return ;
 }

C.假算法天下第一

搞了半天 搞懂了题意，就是一个数组分k次（至多），然后要求每部分尽量小，再求这k个部分的最大值。

emmm就是一个最大值最小化问题，LRJ的《算法入门经典》里面有详细介绍。

我们可以用二分思考这道题，我们使用二分确定一个值x，使得x尽量小并且每个区间都不大于它。

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 #define pi (acos(-1))
 int n,k;
 ll p[];
 bool flag[];

 void work(ll l, ll r) {
     while(l < r) {
         bool flag1 = false;
         ll mid = (l + r) / ;
         ll sum = , kide = ;

         for(int i = ; i < n; i++) {
             if(sum < mid && sum + p[i] < mid) {
                 sum += p[i];
             }
             else {
                 if(p[i] < mid) {
                     kide++;
                     sum = ;
                     sum += p[i];
                 } else {
                     flag1 = true;
                     break;
                 }
             }
         }

         if(flag1 || kide > k) {
             l = mid + ;
         } else {
             r = mid;
         }
     }

     ll sum = ;

     for(int i = n - ; i >= ; i--) {
         if(sum < l && sum + p[i] < l) {
             sum += p[i];
         }
         else {
             sum = ;
             flag[i] = true;
             sum += p[i];
         }
     }

     int di = ;
     int pos = ;

     for(int i = n - ; i >= ; i--) {
         if(flag[i]) {
             di++;
         }
     }

     if(di != k) {
         for(int i = ; i < n && di != k; i++) {
             if(!flag[i]) {
                 flag[i] = true;
                 di++;
             }
         }
     }

     ll tmp = , ans = ;

     for(int i = ; i < n; i++) {
         if(flag[i] && i != n - ) {
             tmp += p[i];
             ans = max(tmp, ans);
             tmp = ;
         } else if(i != n - ) {
             tmp += p[i];
         } else {
             tmp += p[i];
         }
         //cout << tmp << endl;
     }

     ans = max(tmp, ans);
     cout << ans << endl;
 }

 void solve() {
     cin >> n >> k;
     n--;
     ll sum = ;

     for(int i = ; i < n; i++) {
         cin >> p[i];
         sum += p[i];
     }
     if (k == ) {
         cout << sum << endl;
     } else {
         work(, sum);
     }
 }

 int main() {
     ios_base::sync_with_stdio();
     cin.tie();
     solve();
     return ;
 }

然后我发现了个神奇的代码

ZB果然nb = =

D.美好的一天从WA+1开始

题意就不说了，反悔贪心的题目，首先我们按照日期进行贪心，然后用堆维护一下选区的物品，当遇到某件物品不能选取但是他的值却大于以前选过的某个，就进行替换。

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 #define pi (acos(-1))
 int n;
 int na,nb;
 vector<pair<int,int>> p();
 ll sum,avg;

 void init() {
 }

 void solve() {
     while (cin >> n) {
         sum = ;
         priority_queue<int,vector<int>,greater<int>> q;
         for (int i = ; i <= n; i++) {
             cin >> p[i].second >> p[i].first;
         }
         sort(p.begin()+,p.begin()++n);
         for (int i = ; i <= n; i++) {
             if (q.size() < p[i].first) {
                 q.push(p[i].second);
                 sum += p[i].second;
             } else {
                 if (p[i].second > q.top()) {
                     sum -= q.top();
                     sum += p[i].second;
                     q.pop();
                     q.push(p[i].second);
                 }
             }
         }
         cout << sum << endl;
     }
 }

 int main() {
     ios_base::sync_with_stdio();
     cin.tie();
     solve();
     return ;
 }

E.矮死 发 矮死 破色波

没什么好说的，优先喝b就行了。

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 #define pi (acos(-1))
 int n,a,b;
 int na,nb;
 int p[];

 void solve() {
     cin >> n >> a >> b;
     na = a;
     nb = b;
     for (int i = ; i <= n; i++) {
         cin >> p[i];
     }
     for (int i = ; i <= n; i++) {
         if (p[i]) {
             if (na >  && nb < b) {
                 na--;
                 nb++;
             } else if (nb > ) {
                 nb--;
             } else if (na > ) {
                 na--;
             } else {
                 cout << i- << endl;
                 return;
             }
         } else {
             if (nb > ) {
                 nb--;
             } else if (na > ) {
                 na--;
             } else {
                 cout << i- << endl;
                 return;
             }
         }
     }
     cout << n << endl;
 }

 int main() {
     ios_base::sync_with_stdio();
     cin.tie();
     solve();
     return ;
 }

---

排版乱糟糟的，好久没写博客了= =，数学公式将就着看看吧= =，我也不知道博客园怎么弄Latex。