【深度学习】BP反向传播算法Python简单实现

转载：火烫火烫的

个人觉得BP反向传播是深度学习的一个基础，所以很有必要把反向传播算法好好学一下
得益于一步一步弄懂反向传播的例子这篇文章，给出一个例子来说明反向传播
不过是英文的，如果你感觉不好阅读的话，优秀的国人已经把它翻译出来了。
一步一步弄懂反向传播的例子（中文翻译）

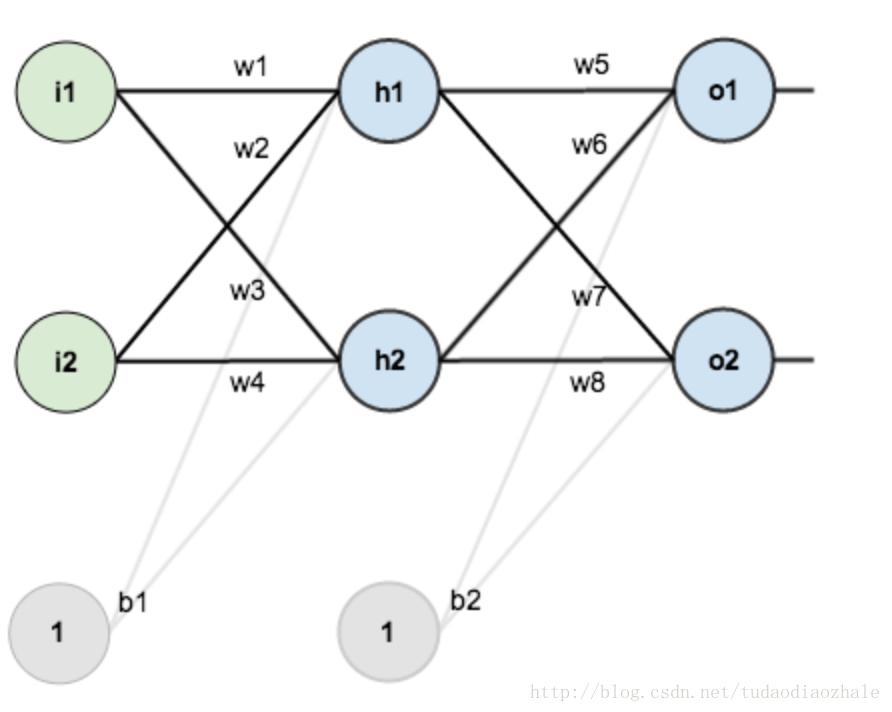
然后我使用了那个博客的图片。这次的目的主要是对那个博客的一个补充。但是首先我觉得先用面向过程的思想来实现一遍感觉会好一点。

随便把文中省略的公式给大家给写出来。大家可以先看那篇博文

 import numpy as np

 # "pd" 偏导
 def sigmoid(x):
     return 1 / (1 + np.exp(-x))

 def sigmoidDerivationx(y):
     return y * (1 - y)

 if __name__ == "__main__":
     #初始化
     bias = [0.35, 0.60]
     weight = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55]
     output_layer_weights = [0.4, 0.45, 0.5, 0.55]
     i1 = 0.05
     i2 = 0.10
     target1 = 0.01
     target2 = 0.99
     alpha = 0.5 #学习速率
     numIter = 10000 #迭代次数
     for i in range(numIter):
         #正向传播
         neth1 = i1*weight[1-1] + i2*weight[2-1] + bias[0]
         neth2 = i1*weight[3-1] + i2*weight[4-1] + bias[0]
         outh1 = sigmoid(neth1)
         outh2 = sigmoid(neth2)
         neto1 = outh1*weight[5-1] + outh2*weight[6-1] + bias[1]
         neto2 = outh2*weight[7-1] + outh2*weight[8-1] + bias[1]
         outo1 = sigmoid(neto1)
         outo2 = sigmoid(neto2)
         print(str(i) + ", target1 : " + str(target1-outo1) + ", target2 : " + str(target2-outo2))
         if i == numIter-1:
             print("lastst result : " + str(outo1) + " " + str(outo2))
         #反向传播
         #计算w5-w8(输出层权重)的误差
         pdEOuto1 = - (target1 - outo1)
         pdOuto1Neto1 = sigmoidDerivationx(outo1)
         pdNeto1W5 = outh1
         pdEW5 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W5
         pdNeto1W6 = outh2
         pdEW6 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W6
         pdEOuto2 = - (target2 - outo2)
         pdOuto2Neto2 = sigmoidDerivationx(outo2)
         pdNeto1W7 = outh1
         pdEW7 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W7
         pdNeto1W8 = outh2
         pdEW8 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W8

         # 计算w1-w4(输出层权重)的误差
         pdEOuto1 = - (target1 - outo1) #之前算过
         pdEOuto2 = - (target2 - outo2)  #之前算过
         pdOuto1Neto1 = sigmoidDerivationx(outo1)    #之前算过
         pdOuto2Neto2 = sigmoidDerivationx(outo2)    #之前算过
         pdNeto1Outh1 = weight[5-1]
         pdNeto2Outh2 = weight[7-1]

         pdEOuth1 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh1 + pdEOuto2 * pdOuto2Neto2 * pdNeto1Outh1
         pdOuth1Neth1 = sigmoidDerivationx(outh1)
         pdNeth1W1 = i1
         pdNeth1W2 = i2
         pdEW1 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W1
         pdEW2 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W2
         pdNeto1Outh2 = weight[6-1]
         pdNeto2Outh2 = weight[8-1]
         pdOuth2Neth2 = sigmoidDerivationx(outh2)
         pdNeth2W3 = i1
         pdNeth2W4 = i2
         pdEOuth2 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh2 + pdEOuto2 * pdOuto2Neto2 * pdNeto2Outh2
         pdEW3 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W3
         pdEW4 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W4
         #权重更新
         weight[1-1] = weight[1-1] - alpha * pdEW1
         weight[2-1] = weight[2-1] - alpha * pdEW2
         weight[3-1] = weight[3-1] - alpha * pdEW3
         weight[4-1] = weight[4-1] - alpha * pdEW4
         weight[5-1] = weight[5-1] - alpha * pdEW5
         weight[6-1] = weight[6-1] - alpha * pdEW6
         weight[7-1] = weight[7-1] - alpha * pdEW7
         weight[8-1] = weight[8-1] - alpha * pdEW8
         # print(weight[1-1])
         # print(weight[2-1])
         # print(weight[3-1])
         # print(weight[4-1])
         # print(weight[5-1])
         # print(weight[6-1])
         # print(weight[7-1])
         # print(weight[8-1])

不知道你是否对此感到熟悉一点了呢？反正我按照公式实现一遍之后深有体会，然后用向量的又写了一次代码。
接下来我们要用向量来存储这些权重，输出结果等，因为如果我们不这样做，你看上面的例子就知道我们需要写很多w1,w2等，这要是参数一多就很可怕。
这些格式我是参考吴恩达的格式，相关课程资料->吴恩达深度学习视频。

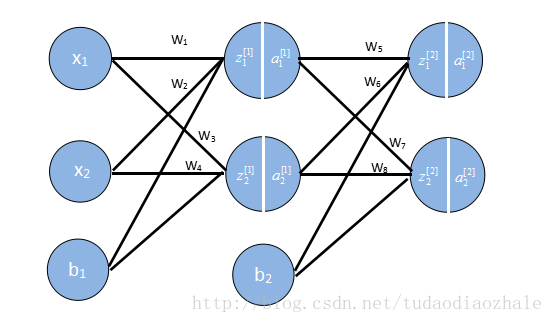
 import numpy as np

 def sigmoid(x):
     return 1 / (1 + np.exp(-x))
 def sigmoidDerivationx(y):
     return y * (1 - y)

 if __name__ == '__main__':
     # 初始化一些参数
     alpha = 0.5
     numIter = 1000000 #迭代次数
     w1 = [[0.15, 0.20], [0.25, 0.30]]  # Weight of input layer
     w2 = [[0.40, 0.45], [0.50, 0.55]]
     # print(np.array(w2).T)
     b1 = 0.35
     b2 = 0.60
     x = [0.05, 0.10]
     y = [0.01, 0.99]
     # 前向传播
     z1 = np.dot(w1, x) + b1     # dot函数是常规的矩阵相乘
     a1 = sigmoid(z1)

     z2 = np.dot(w2, a1) + b2
     a2 = sigmoid(z2)
     for n in range(numIter):
         # 反向传播 使用代价函数为C=1 / (2n) * sum[(y-a2)^2]
         # 分为两次
         # 一次是最后一层对前面一层的错误

         delta2 = np.multiply(-(y-a2), np.multiply(a2, 1-a2))
         # for i in range(len(w2)):
         #     print(w2[i] - alpha * delta2[i] * a1)
         #计算非最后一层的错误
         # print(delta2)
         delta1 = np.multiply(np.dot(np.array(w2).T, delta2), np.multiply(a1, 1-a1))
         # print(delta1)
         # for i in range(len(w1)):
             # print(w1[i] - alpha * delta1[i] * np.array(x))
         #更新权重
         for i in range(len(w2)):
             w2[i] = w2[i] - alpha * delta2[i] * a1
         for i in range(len(w1)):
             w1[i] = w1[i] - alpha * delta1[i] * np.array(x)
         #继续前向传播，算出误差值
         z1 = np.dot(w1, x) + b1
         a1 = sigmoid(z1)
         z2 = np.dot(w2, a1) + b2
         a2 = sigmoid(z2)
         print(str(n) + " result:" + str(a2[0]) + ", result:" +str(a2[1]))
         # print(str(n) + "  error1:" + str(y[0] - a2[0]) + ", error2:" +str(y[1] - a2[1]))

可以看到，用向量来表示的话代码就简短了非常多。但是用了向量化等的方法，如果不太熟，去看吴恩达深度学习的第一部分，再返过来看就能懂了。