CH 4701 - 天使玩偶 - [CDQ分治]
题目链接:传送门


关于CDQ分治(参考李煜东《算法竞赛进阶指南》):
对于一系列操作,其中的任何一个询问操作,其结果必然等价于:初始值 + 此前所有的修改操作产生的影响。
假设共有 $m$ 次操作,对于任意的满足 $1 \le l \le r \le m$ 的正整数 $l,r$,定义 $solve(l,r)$ 为:对于任意的正整数 $k \in [l,r]$,若第 $k$ 次操作为询问操作,则计算第 $l \sim k-1$ 次操作中的修改操作对第 $k$ 次查询的影响。$solve(l,r)$ 可以通过分治来计算:
- 设 $mid = (l+r)>>1$,递归计算 $solve(l,mid)$ 和 $solve(mid+1,r)$。
- 计算第 $l \sim mid$ 次操作中所有修改操作对第 $mid+1 \sim r$ 次操作中所有询问操作的影响。
同时,根据 $solve(l,r)$ 的定义,显然 $solve(1,m)$ 即为原始问题(不考虑初始值的情况下),而当 $l=r$ 时 $solve(l,r)$ 显然不需要进行任何计算。
第 2 部分的操作,其实是一个静态问题,因为修改和询问是完全被前后分开的。类比于经典分治算法归并排序,我们只要让计算第 2 部分的时间复杂度只和 $r-l$ 线性相关,就可以使得总的时间复杂度为 $O(m \log m)$。
这种离线分治算法是基于时间顺序对操作序列进行分治的,因此称为基于时间的分治算法,或者更加广泛的名称CDQ分治。
题解:
这个题,剥离题目背景,无非就是在二维平面上,在若干时刻放置一个点在某个位置,同时在若干时刻查询某个位置与其最近邻的距离。
自然而然就会想起KDTree,不过我还不会带修改的KDTree怎么办,那不妨考虑一下一个简单的问题,假设没有修改操作,只在一开始就给定你平面上若干个点,后续全部都是查询操作。
即:给定平面上 $n$ 个点 $(x_i,y_i)$,有 $m$ 次查询操作,每次询问距离 $(x,y)$ 位置的最近的点有多远(KDTree板子题)。显然,答案就是 $\min_{1 \le i \le n}\{ |x - x_i| + |y - y_i| \}$。
方便起见,为了去掉绝对值符号,不妨把询问变成询问四个方向(第 $1,2,3,4$ 象限方向)上距离最近的点。那么,以第三象限方向上的询问为例,其答案就变成:
$\min_{1 \le i \le n}\{ x - x_i + y - y_i \} = (x+y) - \max_{1 \le i \le n}\{x_i + y_i\}$
其中,$\forall x_i,y_i$ 满足 $x_i \le x$ 且 $y_i \le y$。
此时,可以考虑树状数组优化时间复杂度,先把所有平面上的点和询问中的位置按横坐标从小到大排个序,然后依次进行扫描。
- 若扫描到一个点 $(x_i,y_i)$,则在树状数组中把第 $y_i$ 个位置上的值和 $x_i+y_i$ 取较大值。
- 若扫描到一个询问的位置 $(x,y)$,则在树状数组中查询区间 $[0,y]$ 上的最大值。
显然,按照横坐标从小到大扫描,使得每次询问时,树状数组中存储的值都是 $x$ 值不大于当前位置的点,而在区间 $[0,y]$ 的查询就迫使所有被考虑的点的 $y$ 值都是不超过当前位置的。
时间复杂度 $O((n+m)\log(n+m))$。
然后,我们回到原来的问题,对于原问题,我们使用CDQ分治,那么需要考虑的问题就变成了 $solve(l,r)$ 中,如何计算第 $l \sim mid$ 次操作中所有修改操作对第 $mid+1 \sim r$ 次操作中所有询问操作的影响。换句话说,如何计算第 $l \sim mid$ 次操作中所有添加进来的点,对第 $mid+1 \sim r$ 次操作中所有询问的影响。这样一看,这不就是上面讲到的简化版问题吗。
当然,为了保证每次计算静态问题的时间复杂度仅和 $r-l$ 相关,不能每次都建立一个新的树状数组,必须在每次计算 $solve(l,r)$ 后,把对树状数组的修改都撤销掉。也就是说,要保证对于每个 $solve(l,r)$,在进入和离开函数时,树状数组都是空的。
这样一来,不妨把初始的 $n$ 个点也看做修改操作,对于总的 $n+m$ 次操作,总时间复杂度就是 $O((n+m) \log^2 (n+m))$。
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e6+;
const int INF=0x3f3f3f3f; int n,m;
struct Rec{
int t,x,y;
Rec(){}
Rec(int _t,int _x,int _y) {
t=_t, x=_x, y=_y;
}
bool operator<(const Rec &b)const
{
if(x==b.x) return y<b.y;
else return x<b.x;
}
}o[MAX];
int tot;
Rec s[MAX];
int ans[MAX]; int C[MAX],N;
inline int lowbit(int x){return x&-x;}
int ask(int pos) {
int res=-INF;
for(;pos>=;pos-=lowbit(pos)) res=max(res,C[pos]);
return res;
}
void upd(int pos,int val) {
for(;pos<=N;pos+=lowbit(pos)) C[pos]=max(C[pos],val);
} //第一象限:- x - y - max(- xi - yi)
//第二象限:+ x - y - max(+ xi - yi)
//第三象限:+ x + y - max(+ xi + yi)
//第四象限:- x + y - max(- xi + yi)
void calc(int st,int ed,int d,int sx,int sy)
{
for(int i=st;i!=ed;i+=d)
{
int pos=(sy==)?s[i].y:N-s[i].y;
int val=sx*s[i].x+sy*s[i].y;
if(o[s[i].t].t==) upd(pos,val);
else ans[s[i].t]=min(ans[s[i].t],val-ask(pos));
}
for(int i=st;i!=ed;i+=d)
{
int pos=(sy==)?s[i].y:N-s[i].y;
if(o[s[i].t].t==) for(;pos<=N;pos+=lowbit(pos)) C[pos]=-INF;
}
} void cdqdiv(int l,int r)
{
if(l>=r) return;
int mid=(l+r)>>;
cdqdiv(l,mid);
cdqdiv(mid+,r);
tot=;
for(int i=l;i<=mid;i++) if(o[i].t==) s[++tot]=Rec(i,o[i].x,o[i].y);
for(int i=mid+;i<=r;i++) if(o[i].t==) s[++tot]=Rec(i,o[i].x,o[i].y);
sort(s+,s+tot+);
calc(tot,,-,-,-); //第一象限
calc(,tot+,,,-); //第二象限
calc(,tot+,,,); //第三象限
calc(tot,,-,-,); //第四象限
} int main()
{
scanf("%d%d",&n,&m); m+=n;
for(int i=;i<=n;i++) o[i].t=, scanf("%d%d",&o[i].x,&o[i].y), ++o[i].y;
for(int i=n+;i<=m;i++) scanf("%d%d%d", &o[i].t,&o[i].x,&o[i].y), ++o[i].y; for(int i=;i<=m;i++) N=max(N,o[i].y); N++;
for(int i=;i<=N;i++) C[i]=-INF; memset(ans,0x3f,sizeof(ans));
cdqdiv(,m);
for(int i=;i<=m;i++) if(o[i].t==) printf("%d\n",ans[i]);
}
CH 4701 - 天使玩偶 - [CDQ分治]的更多相关文章
- [BZOJ2716] [Violet 3]天使玩偶(CDQ分治)
[BZOJ2716] [Violet 3]天使玩偶(CDQ分治) 题面 Ayu 在七年前曾经收到过一个天使玩偶,当时她把它当作时间囊埋在了地下.而七年后 的今天,Ayu 却忘了她把天使玩偶埋在了哪里, ...
- BZOJ 2716: [Violet 3]天使玩偶( CDQ分治 + 树状数组 )
先cdq分治, 然后要处理点对答案的贡献, 可以以询问点为中心分成4个区域, 然后去掉绝对值(4种情况讨论), 用BIT维护就行了. --------------------------------- ...
- 洛谷P4169 天使玩偶 CDQ分治
还是照着CDQ的思路来. 但是有一些改动: 要求4个方向的,但是可爱的CDQ分治只能求在自己一个角落方向上的.怎么办?旋转!做4次就好了. 统计的不是和,而是——max!理由如下: 设当前点是(x,y ...
- 天使玩偶:CDQ分治
这道好(du)题(liu)还是很不错的 挺锻炼代码能力和不断优化 卡常的能力的. 对于 每次询问 我都可以将其分出方向 然后 写 也就是针对于4个方向 左下 左上 右下 右上 这样的话 就成功转换了问 ...
- [bzoj] 2716 天使玩偶 || CDQ分治
原题 已知n个点有天使玩偶,有m次操作: 操作1:想起来某个位置有一个天使玩偶 操作2:询问离当前点最近的天使玩偶的曼哈顿距离 显然的CDQ问题,三维分别为时间,x轴,y轴. 但是这道题的问题在于最近 ...
- BZOJ 2716 Violet 3 天使玩偶 CDQ分治
题目大意:初始给定平面上的一个点集.提供两种操作: 1.将一个点增加点集 2.查询距离一个点最小的曼哈顿距离 K-D树是啥...不会写... 我仅仅会CDQ分治 对于一个询问,查询的点与这个点的位置关 ...
- BZOJ.2716.[Violet3]天使玩偶(CDQ分治 坐标变换)
题目链接 考虑对于两个点a,b,距离为|x[a]-x[b]|+|y[a]-y[b]|,如果a在b的右上,那我们可以把绝对值去掉,即x[a]+y[a]-(x[b]+y[b]). 即我们要求满足x[b]& ...
- BZOJ 2716 [Violet 3]天使玩偶 (CDQ分治、树状数组)
题目链接: https://www.lydsy.com/JudgeOnline/problem.php?id=2716 怎么KD树跑得都那么快啊..我写的CDQ分治被暴虐 做四遍CDQ分治,每次求一个 ...
- CH4701 天使玩偶
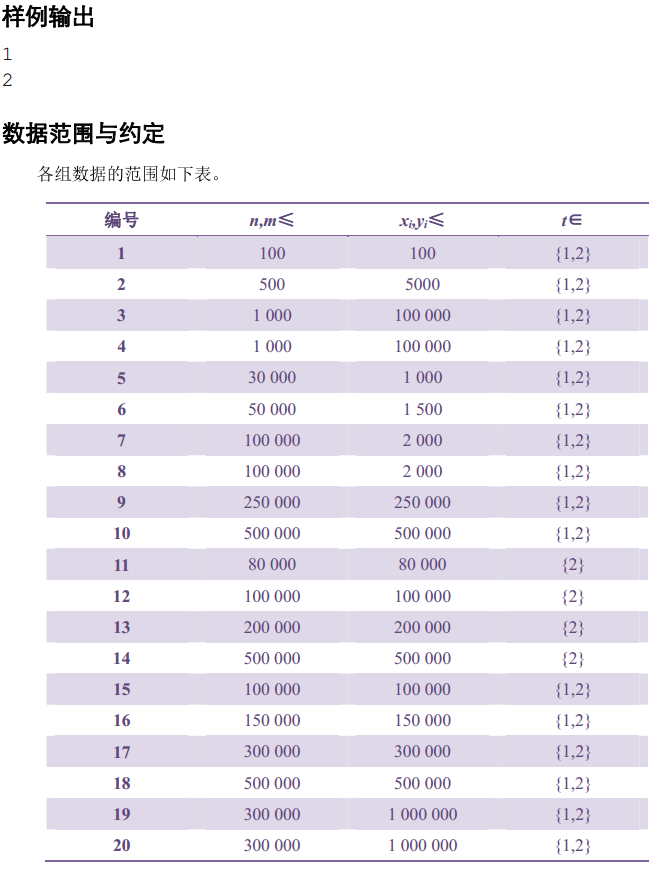
题意 4701 天使玩偶 0x40「数据结构进阶」例题 描述 题目PDF 样例输入 2 3 1 1 2 3 2 1 2 1 3 3 2 4 2 样例输出 1 2 来源 石家庄二中Violet 3杯省选 ...
随机推荐
- 带参数的sigmoid
$y=\frac{1}{1+e^{-(\alpha\times x+\beta)}}$ alpha越大,曲线越陡峭,beta控制平移 import numpy as np import pylab a ...
- mysql数据库分区功能及实例详解
分区听起来怎么感觉是硬盘呀,对没错除了硬盘可以分区数据库现在也支持分区了,分区可以解决大数据量的处理问题,下面一起来看一个mysql数据库分区功能及实例详解 一,什么是数据库分区 前段时间写过一篇 ...
- Lua:Nginx Lua环境配置,第一个Nginx Lua代码
一.编译安装LuaJIT Lua:编译安装LuaJIT,第一个Lua程序 http://blog.csdn.net/guowenyan001/article/details/48250427 二.下载 ...
- StringUtils类中isEmpty与isBlank的区别
org.apache.commons.lang.StringUtils类提供了String的常用操作,最为常用的判空有如下两种isEmpty(String str)和isBlank(String st ...
- openssl - 数字证书的编程解析
原文链接: http://www.cangfengzhe.com/wangluoanquan/37.html 这篇文章主要介绍PKI公钥体系中非常核心元素——数字证书的编程解析.在SSL,SET等安全 ...
- Android使用腾讯浏览服务X5内核
[前期准备] 腾讯X5 jar包下载地址 [点击打开] 本次完整DEMO源码 [打开Github] [集成步骤] 第一步:下载jar包添加到项目 第二步:添加权限 <uses-permissio ...
- ceph crush 之 crush_do_rule
crush_do_rule中,用了一个scratch空间来完成item的搜索. scratch空间总共有3个max_result这么大,并且按照max_result长度划分为三个部分(下图中的a. ...
- 【Java】Comparable和Comparator接口的区别
Java提供了只包含一个compareTo()方法的Comparable接口.这个方法可以个给两个对象排序.具体来说,它返回负数,0,正数来表明已经存在的对象小于,等于,大于输入对象. Java提供了 ...
- 【Ubuntu】PHP环境安装-phpstudy for linux版
安装: wget -c http://lamp.phpstudy.net/phpstudy.bin chmod +x phpstudy.bin #权限设置sudo ./phpstudy.bin ...
- elasticsearch和mysql排序问题
elasticsearch 字段类型错误 最近用elasticseach做排序,排序字段是float型的,没有使用mapping,是直接写代码导入的,没想到排序时如果有小数和整数就会出现错误. 于是查 ...
