DP大大大大大赏

还是前置：

动态规划的三种实现方法：

递推，递归，记忆化搜索

然后还是从斐波那契数列开始引入：

两种求斐波那契数列的方法：

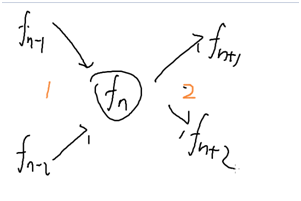
1.用其他位置的结果得到自己的结果：

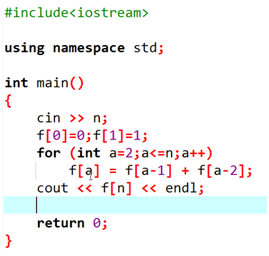
2.用自己的结果算其他的结果；

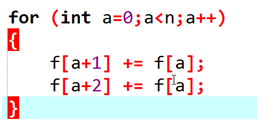
以上两种方法都需要掌握，不同的题对应不同的写法；

3.记忆化搜索（虽然zhx说不是特别重要但lz比较喜欢写的）

没有记忆化之前：O（f[n]）与2^n差不多是一个级别的；

记忆化之后：

DP的一些一些要求：

无后效性：所有状态之间组成了一个DAG

阶段性：

转移方程：怎么算这个东西

状态：要算的东西对应的东西

乱序转移：

把所有状态当做点，所有转移当做边，然后进行拓扑排序；

要讲的几种DP：

l  数位DP

l  树形DP

l  状压DP

l  博弈论DP

l  区间DP

l  背包

乱序宣讲：

1.背包问题：

先看一个最简单的问题：

problem 1：

N个物品，M容量，每个物品都有体积和价值，最大化价值和；

典型的01背包问题，比较经典的例题是采药；

两种方法：1.用自己更新别人：

不选第i个物品，体积不变：f[i+1][j]=f[i][j]

选择第i+1个物品，体积增加：f[i+1][j+v_i+1]=f[i][j]+w_i+1

2.别人更新自己：

f[i][j]=max(f[i-1][j],f[i-1][j-vi]+wi)分别对应不选/选第i个物品；

#include<iostream>

using namespace std;

int n,m,w[],v[];
int f[][];

int main()
{
    cin >> n >> m;
    for (int a=;a<=n;a++)
        cin >> v[a] >> w[a];
    for (int i=;i<=n;i++)
        for (int j=;j<=m;j++)
        {
            f[i][j] = f[i-][j];
            if (j >= v[i]) f[i][j] = max(f[i][j],f[i-][j-v[i]]+w[i]);
        }
    int ans=;
    for (int a=;a<=m;a++)
        ans = max(ans,f[n][a]);
    cout << ans << endl;
    return ;
}

problem 2：（完全背包）

每个物品可以用无限次：

朴素的想法：

枚举第i个物品放了多少个；

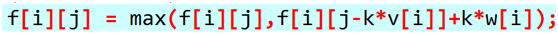
但是显然O（n^3）不够优；

考虑优化：

f[i][j]来说，上面的思路是有i-1行的某个数转移过来的，但实际上我们并不需要这样枚举转移，我们可以从左侧转移，假设当前已经选了一个x物品了，如果我们由左边更新过来，那可能我们算到的正是已经选择过一个x物品的状态，这样，背包就变成无限的啦；

修改代码：

变成了可以由同一行转移过来，横着转移x次<=>我用了x个第i个物品；

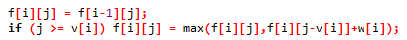
problem 3：（多重背包）

如果每个物品可以用有限次？

考虑像完全背包一样枚举使用物品个数：

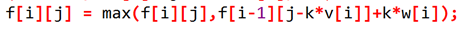
尝试优化：

vi*13：

造物品：

1. 体积为vi只能用1次的物品，
2. 体积为2vi只能用1次的物品；
3. 体积为4vi只能用1次的物品；
4. 体积为6vi只能用1次的物品；
5. 可以把所有1~13内的体积表示出来

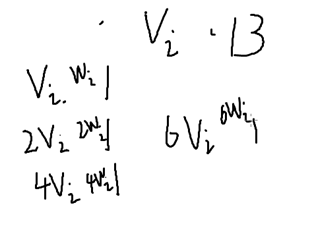
=>转化为01背包；

O（n^2*k）

怎么变成若干捆绑包？

先用二进制表示，不足二进制的再用总的减去

发现k≈logn

复杂度O(nmlogn)

绿框即为凑不够一个二进制然后减下来的

为什么可以把所有数表示出来？

恰好可以表示为x个二进制数：

这样对于每一位都有0/1两种情况，1~31的每个数，都可以写成5位内的二进制，然后每一位只有0和1嘛，显然都可以通过上面算出来，对于不是恰好拆分成二进制的，可以先不看最后的数，然后看成1~31+x；

造捆绑包：

基础DP：

problem 1：

• 数字三角形
• 给你一个三角形
• 问从怎么走能够取得最大代价

每次可以向下或向右下走，使得走过的这条路，所有数字之和最大；

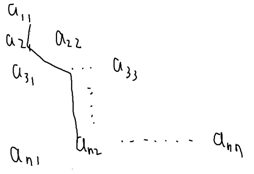
正着推：f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j];最后要枚举最后一行哪一guo最大；

突然安利的oj：joyoi

数字三角形2：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define mod 100

using namespace std;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch>''||ch<'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
int a[][];
bool f[][][];

int main(){
    n=read();
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            a[i][j]=read();
    f[][][a[][]%mod]=;
    for(int i=;i<=n;i++){
        for(int j=;j<=i;j++){
            for(int k=;k<;k++){
                f[i][j][k]=(f[i-][j-][(k-a[i][j]+mod)%mod]|f[i-][j][(k-a[i][j]+mod)%mod]);
            }
        }
    }
    bool bj=;
    for(int k=;k>=;k--){
        for(int i=;i<=n;i++){
            if(f[n][i][k]){
                printf("%d",k);
                bj=;
                break;
            }
        }
        if(bj==)
                break;
    }
    return ;
}

自己更新别人，因此只需要算到n-1行；

当状态是可行的我们才用它更新别人；

转移啊：

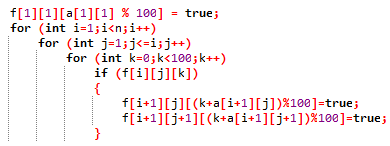
最后计算答案：

枚举最后一行走到哪一列，然后枚举走出来的和%100是多少。

#include<iostream>
#include<cstdio>
#include<algorithm>
#define mod 100

using namespace std;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch>''||ch<'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n;
int a[][];
bool f[][][];

int main(){
    n=read();
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            a[i][j]=read();
    f[][][a[][]%mod]=;
    for(int i=;i<n;i++){
        for(int j=;j<=i;j++){
            for(int k=;k<;k++){
                if(f[i][j][k]){
                    f[i+][j][(k+a[i+][j])%mod]=;
                    f[i+][j+][(k+a[i+][j+])%mod]=;
                }
            }
        }
    }
    int ans=;
    for(int i=;i<=n;i++)
        for(int k=;k<;k++)
            if(f[n][i][k])
                ans=max(ans,k);
    printf("%d",ans);
    return ;
}

最长上升子序列；

当n>=10^5，第二层j的枚举可以用线段树来做；

有时可以用数据结构优化DP

f[i]表示以第i个数结尾的最长上升子序列的长度，那么f[i]=max(f[j])+1,其中1<=j<i;

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch>''||ch<'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,ans;
int p[],f[];

int main(){
    n=read();
    for(int i=;i<=n;i++){
        p[i]=read();
    }
    f[]=;p[]=-;
    for(int i=;i<=n;i++){
        for(int j=;j<i;j++){
            if(p[i]>p[j]) f[i]=max(f[i],f[j]);
        }
        f[i]+=;
    }
    for(int i=;i<=n;i++) ans=max(ans,f[i]);
    printf("%d",ans);
    return ;
}

区间DP：

区间DP特征：给n个东西，每次只能合并两个相邻的东西；

最最最最最典型的例子，石子合并

合并的顺序不同，代价也不同；

f[l][r]把第l堆石子到第r堆石子合并成一堆的最小代价是多少；

f[l][l]=0；

合并[l,r]

我们可以找到一个分界线，先将分界线左边的石子合并为一堆，然后右边的合并成一堆，最后再将这两堆合并成一堆（将这两堆合并的代价是这一段石子的区间和）：

然后维护前缀和来计算区间和；

注意要枚举区间长度，然后枚举左端点，计算右端点；

切不可两层循环枚举左右端点；

一个有关矩阵乘法的问题：

矩阵乘法

自定义顺序

使得运算次数最少

矩阵乘法结合律：

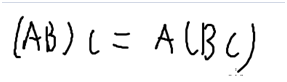
N个矩阵， M1  ,  M2,   M3……Mn

大小为： a1*a2  a2*a3  a3*a4  an*an+1

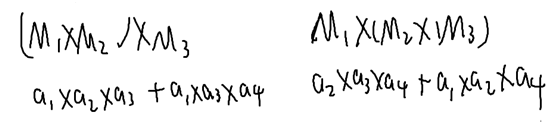
操作：合并两个相邻的矩阵；

目标：合并成一个矩阵；

f[l][r]把第l~第r个矩阵合并成一个矩阵；

f[l][r]=min(f[l][p]+f[p+1][r]+al*a_p+1*a_r+1)；

能量项链的说

状压DP：

n<=20（22）<=>状压

problem 1：p1171

第i个点坐标 xi，yi；

f[s][i]

s:n位的二进制数，已经走到过的点：{1,2,4,6}说明已经走过1,2,4,6点，对应二进制=>101011

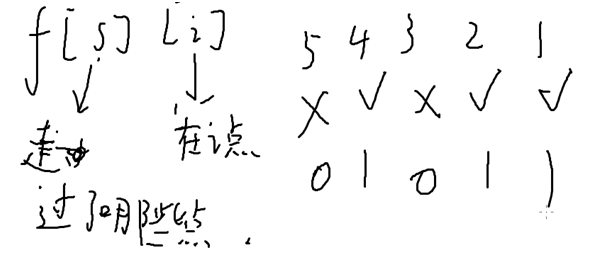
转化为10进制：11=>01011；

常见压缩方法：把数组表示为k进制的数；

转移：枚举一个j，表示第j个点，然后要求j是没走过的；

因为是状压DP，为了方便二进制的表示，我们的循环从0开始。

初始化f数组为为超级大的一个数，然后f[s][i]表示状态s（转化为二进制后1代表已经走了这个数，0代表没有走这个点）并且现在在点i时的最短路径，显然起点1-1时为0（注意点的下标从0开始因此最后都要-1）

然后枚举状态，尝试转移：，j

然后枚举当前走到了哪个点，判断这种状态有没有被更新过，如果被更新过了，我们用它更新其他的点；

枚举接下来走哪个点，要注意判断这个点之前要没有走过，然后更新状态，将新状态赋值；

最后答案是枚举最后走到哪个点，然后加上最后走到的点到起点的距离，取最小，就是最后的答案；

伪代码：

#include<iostream>

using namespace std;

double f[][];
double x[],y[];

int main()
{
    cin >> n;
    for (int a=;a<n;a++)
        cin >> x[a] >> y[a];
    f=∞
    f[][]=;
    for (int s=;s<(<<n);s++)
        for (int i=;i<n;i++)
            if (f[s][i] < ∞)
            {
                for (int j=;j<n;j++)
                    if ( ((s>>j) & ) == )
                    {
                        int news = s | (<<j);
                        f[news][j] = min(f[news][j],f[s][i] + dis(i,j));
                    }
            }
    for (int i=;i<n;i++)
        ans=min(ans, f[(<<n)-][i] + dis(i,));

    return ;
}

problem 2：luogu1879

f[i][s]前i行草已经种完了，这一行的草长成s样时的方案数；

用二进制的数来代表第i行每个位置有没有种草

判断第i行S和第i+1行S’没有相邻的草：S&S’==0；

problem 3：p1896

n<=8

枚举怎么放国王，然后判断是否冲突，因为多了一个恰好，因此我们加一维：f[i][s][j]代表：i与s的表示同上题，j表示现在放了j国王了；

然后判断需要修改一下；

数位DP：

什么是数位DP？难啊

DP时按照数的每一位一位一位进行转移的；

举个栗子：

给定两个数l，r，问从了l~r有多少个数；

显然是ans=r-l+1

1. 往往先进行前缀和转化；

从高位向低位

f[i][1/0] 已经填好第i位  j==0？ now<x:无法确定now（其实就是目前和x长得一样）；

在以上情况这种数有多少个；

考虑下一位要填什么数；

x只有l位，那么y的l+1,l+2……位（个位最小）只能填0，那么填第l+1位和x一样的方案数只有1中（全为0）

填了之后y>x；

problem2：

求[l,r]中的数的数位之和

仍然是维护一个前缀和：

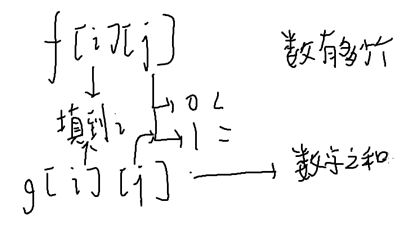
problem 3：BZOJ1026 windy数

f[i][j][k]已经填好了第i位；j：</=；k：第i位填了k

保证第i位和第i+1位的数字大小差至少2；

差不多搞定了？

problem 4：BZOJ2757

K<=10^18;

有一些位置永远不会用到，比如13，存在的只能是<10的质数；

数组大小a：log210^18  b：log310^18  c：log510^18  d：log710^18

再优化：

把所有以上形式

的数算出来，大概有30000多个，预处理出来，然后放到数组中，然后转移f[i][j][k]，表示是这三万多个数中第k个数qwq；

树形DP：

假设为有根树；

从下到上

在每个点，维护以其为根的子树的信息；

problem 1：

求树上有多少个点？

f[i]表示以i为根的子树有多少个点？

problem 2：

求树的直径；

在树上找两个点，使他们距离最远；

从每个点向下走，最长和次长是多少

f[i][0]从i这个点向下走，最长的是多少；

f[i][1]从i这个点向下走，次长的是多少；

然后枚举在每个点转弯的最大值和次大值的和，求一个最大的；

f[i][0]=max(f[p_j][0]) +1 p_j∈son(i);

f[i][1]=max(f[pk][0])+1pk!=pj,pk∈son(i)避免和f[i][0]选到同一个位置去，那么f[p_j][1]不能用了，其余的最长路显然大于次长路，因此只需要在剩余儿子中找一个最大的（总体次大的）；

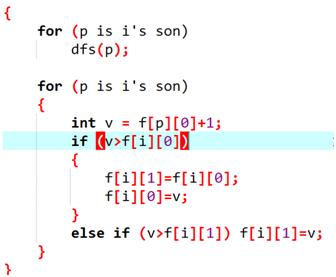
problem 3：

求树上路径总长度和

f[i]表示以i为根的子树有多少个点；

然后

考虑一条边，会被多少条路径经过：

只要保证一个点在子树中，一个点在子树外面选一个点，一定会经过这条边，然后路径可以正着走，也可以反着走，需要*2

problem 4：Poj2342

f[i][0/1] 以i为根的子树中，选出若干个点，权值最大是多少

0=> i没选 1=>i选了；

最后答案：max(f[1][0],f[1][1])

f[i][1]=Σf[j][0]+a[i] j∈son(i)；

f[i][0]=Σmax(f[j][0],f[j][1]) j∈son(i)

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch>''||ch<'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int n,k,l;
int f[][];//1 choose this people/0 do not choose this people
struct node{
    int fa,cnt,r;
    int son[];
}p[];

void dfs(int node){
    if(!p[node].cnt) {
        f[node][]=p[node].r;
        f[node][]=;
        return;
    }

    for(int i=;i<=p[node].cnt;i++){
        dfs(p[node].son[i]);
    }
    for(int i=;i<=p[node].cnt;i++){
        f[node][]+=f[p[node].son[i]][];
        f[node][]+=max(f[p[node].son[i]][],f[p[node].son[i]][]);
    }
    f[node][]+=p[node].r;
}

int main(){
    n=read();
    for(int i=;i<=n;i++) p[i].r=read();
    for(int i=;i<n;i++) {
        l=read();k=read();
        p[l].fa=k;
        p[k].son[++p[k].cnt]=l;
    }
    int s;
    for(int i=;i<=n;i++){
        if(!p[i].fa) dfs(i),s=i;
    }
    printf("%d",max(f[s][],f[s][]));
    return ;
}

迷之MLE，然后把son改小为原来的1/2，居然过了

problem 5：poj1463

f[i][0/1] 以i为根的子树所有节点都被守护(0i没有士兵，1i有士兵)所需最少士兵数量

f[i][0]=Σf[j][1] j∈son(i) //父亲不放士兵，所以儿子一定要放士兵

f[i][1]=Σmin(f[j][0],f[j][1])+1 j∈son(i) //父亲不放士兵，那么儿子放不放无所谓，取放与不放的最小值

up：消防局的设立；luogu2279

守护所有距离不超过2的节点：

f[i][0/1/2]以i为根的子树已经全部覆盖的情况下，i这个点向下走，到达最近的士兵的距离是0/1/2的最小士兵数；

相当于自己放士兵f[i][0]=Σmin(f[j][0/1/2])+1; j∈son(i);

相当于儿子放士兵f[i][1]再跑一个DP来求f[i][1]:

用另一个数组g[j][1/0]；已经确定了前j个儿子的取值，其中这j个儿子中有（1）没有（0）拿出一个0值（到达最近士兵距离为0）来更新答案；

相当于孙子放士兵f[i][2]

另一种解法：

定根之后，找到这棵树中深度最深的叶子节点：

1.自己 2.兄弟 3.父亲 4.爷爷

应该选择哪一种？

显然是4，因为把士兵放在1 2 3位置能覆盖到的所有节点，放在4都可以被覆盖；

找出深度最深的节点，找到他的爷爷，在爷爷的位置放一个士兵，把它爷爷能覆盖到的所有节点直接从树中删掉；

重复直到没有节点；

N堆石子，可以合并任意两堆，合并的代价是两堆的异或和；

状压dp。f[s]把s所对应的石子，合并为1堆的最小代价；

枚举0 2 3 5的一个子集，

枚举每个状态的石子总和

初始化，求最小，所以初始为无穷大。然后只合并一堆代价为0；

枚举s的子集a：

判断a为s的子集：

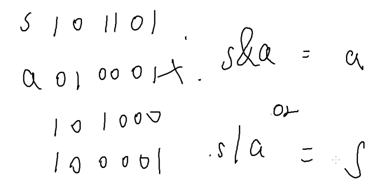
剩下那坨石子：a^s；

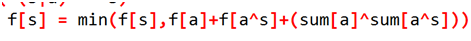
但是，这个算法过不了n=16 O(4^n)

改进：

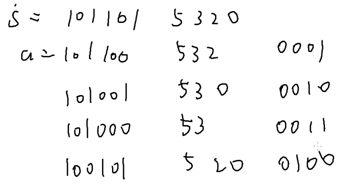
O(3^n)

博弈论DP：

类型1：现在有一个游戏G，两个人玩，回合制，没有平局；胜负的区分方法：当某个人没办法进行操作时，这个人就输了；

然后两个人都绝顶聪明，会做出对自己最最最最有利的操作。

一般问的都是先手是否必胜，或者先手是否必败。

当走到某个状态后，无法再走，则再此点的人一定会输，称为必败态；

因为绝顶聪明，所以左上角的点是必胜态

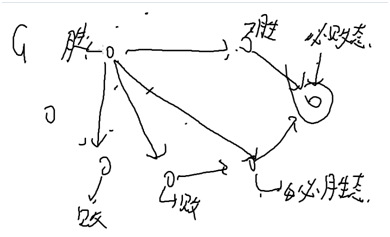
f[s]=1/0 s是一个状态。状态s是否是必胜；

s1~sm如果存在f[si]=0（必败态），则有f[s]=1；

任意f[si]=1,则f[s]=0；

problem 1：

f[i][j]原数还剩下i，对手上一次减了j，这种情况是必胜，还是必败；

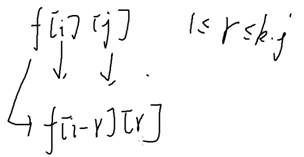
建议用记忆化搜索；

f[i][j]必胜or必败，g[i][j]i，j对应的状态算没算过；

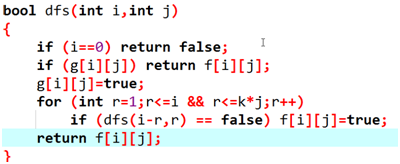
第二类：n个游戏G1，G2……Gn，两个人，回合制，分出胜负，在每个游戏中都不能动的输；

取石子游戏：

n堆石子，a1，a2，……an；Alice and Bob，Alice先手。从某一堆石子中取走任意多个石子，当谁没法取石子，谁就输了

SG函数：

sg[必败态]=0;

此题中：sg[1]=1;sg[2]=2;
sg[x]所有可以转移到状态中的sg没有出现过的最小自然数；

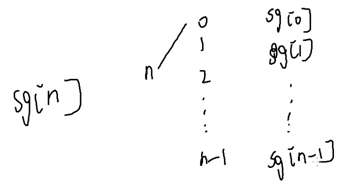
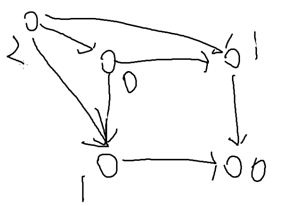
在本题中，sg[n]=n；

如果一个游戏的sg!=0 先手必败；

sg=0先手必败；

SG定理：

n个游戏组合在一起的SG值，等于每个游戏的SG值异或起来；

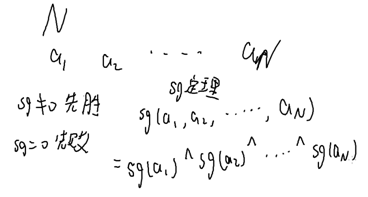
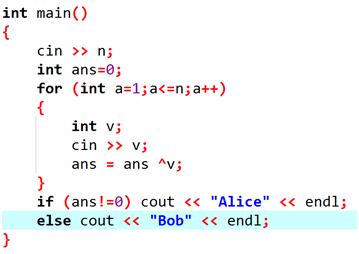
取石子-改：

n堆石子，a1，a2，……an；Alice and Bob，Alice先手。从某一堆石子中取走1~4个石子，当谁没法取石子，谁就输了

sg[ai]=ai%5;

problem 4：

博弈论问题一般：把题目转化为基本的取石子问题；

算出每堆是奇数个还是偶数个，1为奇数，2为偶数；把所有奇数堆的下标取出来，异或起来=0先手必败，！=0先手必胜

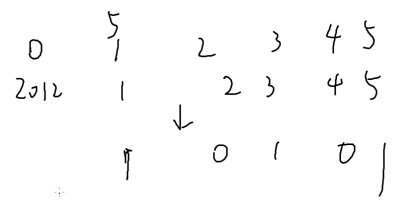
把所有下标为奇数的位置的石子异或起来就是答案：

距离终点为奇数的格子上的棋子异或起来；

f[s] s:n位的二进制数，代表每个位置有没有被标记过，然后炸了。

考虑当做多个游戏

保证先手必胜，则先手涂色的左右两个都不能涂色，将剩余的拆成两个独立的游戏，再将其合并

sg[i]长度为i的横条，sg值是多少

BZOJ2789

f[x][y] =>f[1][x+y]

=>f[2x][y]

=>f[3x][y]

f[a][b][y] x=2^a*3^b;