P5663 加工零件

P5663 加工零件

题解

暴力搜索

搜索显然会TLE

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef long long ll;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1e5+;
struct node{
    int to,nxt;
}edge[maxn*];
int head[maxn],cnt=;
int n,m,q;
bool vis[maxn];//节点i是否与1直接相连
int son[][];
int num[];

void addedge(int u,int v)
{
    edge[++cnt].to =v;edge[cnt].nxt =head[u];head[u]=cnt;
    edge[++cnt].to =u;edge[cnt].nxt =head[v];head[v]=cnt;
}

void dfs(int sum,int u)
{
    if(sum<) return;
    if(num[]==) return;
    for(int v,i=;i<=son[u][];i++){
        v=son[u][i];
        num[v]=min(num[v],sum);
        dfs(sum-,v);
    }
}

int main()
{
    n=read();m=read();q=read();
    vis[]=;
    for(int u,v,i=;i<=m;i++){
        u=read();v=read();
        if(u==) vis[v]=;
        if(v==) vis[u]=;
        son[u][++son[u][]]=v;
        son[v][++son[v][]]=u;
        addedge(u,v);
        addedge(v,u);
    }
    for(int a,l,t=;t<=q;t++){
        memset(num,,sizeof(num));
        a=read();l=read();
        if(l==){
            if(a==||(!vis[a])) {
                printf("No\n");
                continue;
            }
            else if(vis[a]&&a!=) {
                printf("Yes\n");
                continue;
            }
        }else{
            num[a]=l;
            dfs(l-,a);
            if(num[]==) printf("Yes\n");
            else printf("No\n");
        }
    }
    return ;
}

暴力搜索 40pt

考虑正解 SPFA最短路

题目给出一张无向图，他大概长这个亚子

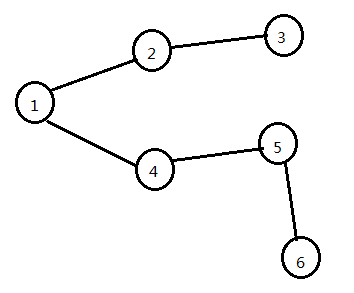
对于给出一个点 a 要完成第  L  阶段任务，也就是从 a 到 1 找一条长度为 L 的路径

我们发现

1.  点2到1的距离为1（奇数），如果2完成奇数阶段任务，那么1就要为它提供原料，如果是偶数阶段任务就不用

2.  点5到点1的距离为2（偶数），如果5完成偶数阶段任务，那么1就要为它提供原料，如果是奇数阶段任务就不用

如果2到1的距离是5，也就是大于他们之间最短距离，那么要完成的阶段就会在二者之间不断传递（2-->5  , 1-->4 , 2-->3  , 1-->2  , ....），最后会变成上面分析的情况1

也就是说

1.  如果点a要完成的任务阶段数大于等于他们之间的最短距离，都可以化简成处理他们之间的最短距离来做

2.  如果a要完成的任务阶段数本就小于他们之间的最短距离，也就是a在扩展到1之前就已经有别的点为它提供原料，1节点自然不用提供原料

我们现在就要考虑上面说的第一种情况 L >= dis(a-->1)

由于从一个节点出发到达1会有很多路径，我们用 dis[ i ][ 0 ] 记录从节点 i 到节点 1 的长度为偶数的最短路的长度，用 dis[ i ][ 1 ] 记录从节点 i 到节点 1 的长度为奇数最短路的长度，SPFA 具体实现

更新数组的柿子也就是：

dis[ v ][ 0 ] = min ( dis[ v ][ 0 ] , dis[ u ][ 1 ] + 1 )

dis[ v ][ 1 ] = min ( dis[ v ][ 1 ] , dis[ u ][ 0 ] + 1 )

综上分析得出结论

1.  点 a 要完成的阶段任务数为偶数， 如果从a-->1存在一条偶数最短路，并且它的长度小于等于该任务数，1需要提供原料

2.  点 a 要完成的阶段任务数为奇数， 如果从a-->1存在一条奇数最短路，并且它的长度小于等于该任务数，1需要提供原料

3.  其余情况就不用1提供原料了

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

typedef long long ll;

int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=1e5+;
int n,m,qus;

struct node{
    int to,nxt;
}edge[maxn<<];
int cnt=,head[maxn];
inline void addedge(int u,int v)
{
    edge[++cnt].to =v,edge[cnt].nxt =head[u],head[u]=cnt;
    edge[++cnt].to =u,edge[cnt].nxt =head[v],head[v]=cnt;
}

int dis[maxn][];
bool vis[maxn];

inline void spfa()
{
    queue<int>q;
    memset(dis,,sizeof(dis));
    memset(vis,,sizeof(vis));
    dis[][]=;
    vis[]=;
    q.push();
    while(!q.empty() ){
        int u=q.front() ;
        q.pop() ;
        vis[u]=;
        for(int v,i=head[u];i;i=edge[i].nxt ){
            v=edge[i].to ;
            if(dis[v][]>dis[u][]+){
                dis[v][]=dis[u][]+;
                if(!vis[v]){
                    q.push(v);
                    vis[v]=;
                }
            }
            if(dis[v][]>dis[u][]+){
                dis[v][]=dis[u][]+;
                if(!vis[v]){
                    q.push(v);
                    vis[v]=;
                }
            }
        }
    }
}

int main()
{
    n=read();m=read();qus=read();
    for(int u,v,i=;i<=m;i++){
        u=read();v=read();
        addedge(u,v);
    }
    spfa();
    for(int a,l,i=;i<=qus;i++){
        a=read();l=read();
        if((l%)&&(dis[a][]<=l))printf("Yes\n");
        else if((l%==)&&(dis[a][]<=l))printf("Yes\n");
        else printf("No\n");
    }
    return ;
}