小书匠 Graph 图论 

学过线性代数的都了解矩阵,在矩阵上的文章可做的很多,什么特征矩阵,单位矩阵等.grpah存储可以使用矩阵,比如graph的邻接矩阵,权重矩阵等,这节主要是在等到graph后,如何快速得到这些信息.详细官方文档在这里

目录:

注意:如果代码出现找不库,请返回第一个教程,把库文件导入.

10线性代数相关

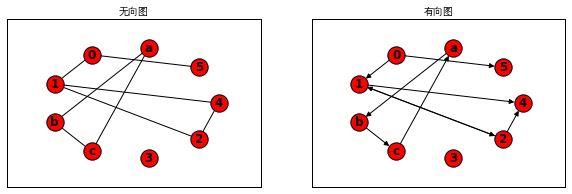
10.1图矩阵

  1. #定义图的节点和边 
  2. nodes=['0','1','2','3','4','5','a','b','c'] 
  3. edges=[('0','0',1),('0','1',1),('0','5',1),('0','5',2),('1','2',3),('1','4',5),('2','1',7),('2','4',6),('a','b',0.5),('b','c',0.5),('c','a',0.5)] 
  5. plt.subplots(1,2,figsize=(10,3)) 
  7. #定义一个无向图和有向图 
  8. G1 = nx.Graph() 
  9. G1.add_nodes_from(nodes) 
  10. G1.add_weighted_edges_from(edges) 
  12. G2 = nx.DiGraph() 
  13. G2.add_nodes_from(nodes) 
  14. G2.add_weighted_edges_from(edges) 
  16. pos1=nx.circular_layout(G1) 
  17. pos2=nx.circular_layout(G2) 
  19. #画出无向图和有向图 
  20. plt.subplot(121) 
  21. nx.draw(G1,pos1, with_labels=True, font_weight='bold') 
  22. plt.title('无向图',fontproperties=myfont) 
  23. plt.axis('on') 
  24. plt.xticks([]) 
  25. plt.yticks([]) 
  27. plt.subplot(122) 
  28. nx.draw(G2,pos2, with_labels=True, font_weight='bold') 
  29. plt.title('有向图',fontproperties=myfont) 
  30. plt.axis('on') 
  31. plt.xticks([]) 
  32. plt.yticks([]) 
  34. plt.show() 
  36. #控制numpy输出小数位数 
  37. import numpy as np 
  38. np.set_printoptions(precision=3)  
  40. #邻接矩阵 
  41. A = nx.adjacency_matrix(G1) 
  42. print('邻接矩阵:\n',A.todense()) 
  44. #关联矩阵 
  45. I = nx.incidence_matrix(G1) 
  46. print('\n关联矩阵:\n',I.todense()) 
  48. #拉普拉斯矩阵 
  49. L=nx.laplacian_matrix(G1) 
  50. print('\n拉普拉斯矩阵:\n',L.todense()) 
  52. #标准化的拉普拉斯矩阵 
  53. NL=nx.normalized_laplacian_matrix(G1) 
  54. print('\n标准化的拉普拉斯矩阵:\n',NL.todense()) 
  56. #有向图拉普拉斯矩阵 
  57. DL=nx.directed_laplacian_matrix(G2) 
  58. print('\n有向拉普拉斯矩阵:\n',DL) 
  60. #拉普拉斯算子的特征值 
  61. LS=nx.laplacian_spectrum(G1) 
  62. print('\n拉普拉斯算子的特征值:\n',LS) 
  64. #邻接矩阵的特征值 
  65. AS=nx.adjacency_spectrum(G1) 
  66. print('\n邻接矩阵的特征值:\n',AS) 
  68. #无向图的代数连通性 
  69. AC=nx.algebraic_connectivity(G1) 
  70. print('\n无向图的代数连通性:\n',AC) 
  72. #图的光谱排序 
  73. SO=nx.spectral_ordering(G1) 
  74. print('\n图的光谱排序:\n',SO) 
  76. #两个矩阵的解释看:https://blog.csdn.net/Hanging_Gardens/article/details/55670356 

图矩阵示例

输出:

  1. 邻接矩阵: 
  2. [[0. 0. 0. 0. 5. 0. 0. 0. 6. ] 
  3. [0. 0. 0. 2. 0. 0. 0. 0. 0. ] 
  4. [0. 0. 0. 0. 0. 0.5 0.5 0. 0. ] 
  5. [0. 2. 0. 1. 1. 0. 0. 0. 0. ] 
  6. [5. 0. 0. 1. 0. 0. 0. 0. 7. ] 
  7. [0. 0. 0.5 0. 0. 0. 0.5 0. 0. ] 
  8. [0. 0. 0.5 0. 0. 0.5 0. 0. 0. ] 
  9. [0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  10. [6. 0. 0. 0. 7. 0. 0. 0. 0. ]] 
  12. 关联矩阵: 
  13. [[1. 1. 0. 0. 0. 0. 0. 0. 0.] 
  14. [0. 0. 1. 0. 0. 0. 0. 0. 0.] 
  15. [0. 0. 0. 1. 1. 0. 0. 0. 0.] 
  16. [0. 0. 1. 0. 0. 1. 0. 0. 0.] 
  17. [0. 1. 0. 0. 0. 1. 0. 1. 0.] 
  18. [0. 0. 0. 1. 0. 0. 0. 0. 1.] 
  19. [0. 0. 0. 0. 1. 0. 0. 0. 1.] 
  20. [0. 0. 0. 0. 0. 0. 0. 0. 0.] 
  21. [1. 0. 0. 0. 0. 0. 0. 1. 0.]] 
  23. 拉普拉斯矩阵: 
  24. [[11. 0. 0. 0. -5. 0. 0. 0. -6. ] 
  25. [ 0. 2. 0. -2. 0. 0. 0. 0. 0. ] 
  26. [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] 
  27. [ 0. -2. 0. 3. -1. 0. 0. 0. 0. ] 
  28. [-5. 0. 0. -1. 13. 0. 0. 0. -7. ] 
  29. [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] 
  30. [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] 
  31. [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  32. [-6. 0. 0. 0. -7. 0. 0. 0. 13. ]] 
  34. 标准化的拉普拉斯矩阵: 
  35. [[ 1. 0. 0. 0. -0.418 0. 0. 0. -0.502] 
  36. [ 0. 1. 0. -0.707 0. 0. 0. 0. 0. ] 
  37. [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] 
  38. [ 0. -0.707 0. 0.75 -0.139 0. 0. 0. 0. ] 
  39. [-0.418 0. 0. -0.139 1. 0. 0. 0. -0.538] 
  40. [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] 
  41. [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] 
  42. [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  43. [-0.502 0. 0. 0. -0.538 0. 0. 0. 1. ]] 
  45. 有向拉普拉斯矩阵: 
  46. [[ 0.889 -0.117 -0.029 -0.087 -0.319 -0.029 -0.029 -0.129 -0.242] 
  47. [-0.117 0.889 -0.026 -0.278 -0.051 -0.026 -0.026 -0.114 -0.056] 
  48. [-0.029 -0.026 0.994 -0.012 -0.009 -0.481 -0.481 -0.025 -0.01 ] 
  49. [-0.087 -0.278 -0.012 0.757 -0.097 -0.012 -0.012 -0.052 -0.006] 
  50. [-0.319 -0.051 -0.009 -0.097 0.994 -0.009 -0.009 -0.041 -0.434] 
  51. [-0.029 -0.026 -0.481 -0.012 -0.009 0.994 -0.481 -0.025 -0.01 ] 
  52. [-0.029 -0.026 -0.481 -0.012 -0.009 -0.481 0.994 -0.025 -0.01 ] 
  53. [-0.129 -0.114 -0.025 -0.052 -0.041 -0.025 -0.025 0.889 -0.045] 
  54. [-0.242 -0.056 -0.01 -0.006 -0.434 -0.01 -0.01 -0.045 0.994]] 
  56. 拉普拉斯算子的特征值: 
  57. [-1.436e-15 0.000e+00 4.610e-16 7.000e-01 1.500e+00 1.500e+00 
  58. 4.576e+00 1.660e+01 2.013e+01] 
  60. 邻接矩阵的特征值: 
  61. [12.068+0.000e+00j 2.588+0.000e+00j -7.219+0.000e+00j -4.925+0.000e+00j 
  62. -1.513+0.000e+00j 1. +0.000e+00j -0.5 +2.393e-17j -0.5 -2.393e-17j 
  63. 0. +0.000e+00j] 
  65. 无向图的代数连通性: 
  66. 0.0 
  68. 图的光谱排序: 
  69. ['4', '2', '1', '0', '5', 'b', 'c', 'a', '3'] 

后面还有两个小节,由于对图论算法不是很明白,所以先讲明白算法原理,再使用networkX实现,如无须读算法,可以跳过算法原理部分.

NetworkX系列教程(9)-线性代数相关的更多相关文章

  1. NetworkX系列教程(1)-创建graph

    小书匠Graph图论 研究中经常涉及到图论的相关知识,而且常常面对某些术语时,根本不知道在说什么.前不久接触了NetworkX这个graph处理工具,发现这个工具已经解决绝大部分的图论问题(也许只是我 ...

  2. NetworkX系列教程(11)-graph和其他数据格式转换

    小书匠 Graph 图论  学过线性代数的都了解矩阵,在矩阵上的文章可做的很多,什么特征矩阵,单位矩阵等.grpah存储可以使用矩阵,比如graph的邻接矩阵,权重矩阵等,这节主要是在等到graph后 ...

  3. NetworkX系列教程(10)-算法之五:广度优先与深度优先

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  4. NetworkX系列教程(10)-算法之四:拓扑排序与最大流问题

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  5. NetworkX系列教程(10)-算法之三:关键路径问题

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  6. NetworkX系列教程(10)-算法之二:最小/大生成树问题

    小书匠 Graph 图论  重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定 ...

  7. NetworkX系列教程(10)-算法之一:最短路径问题

    小书匠Graph图论 重头戏部分来了,写到这里我感觉得仔细认真点了,可能在NetworkX中,实现某些算法就一句话的事,但是这个算法是做什么的,用在什么地方,原理是怎么样的,不清除,所以,我决定先把图 ...

  8. NetworkX系列教程(8)-Drawing Graph

    小书匠Graph图论 如果只是简单使用nx.draw,是无法定制出自己需要的graph,并且这样的graph内的点坐标的不定的,运行一次变一次,实际中一般是要求固定的位置,这就需要到布局的概念了.详细 ...

  9. NetworkX系列教程(2)-graph生成器

    小书匠Graph图论 本节主要讲解如何快速使用内置的方法生成graph,官方的文档在这里,里面包含了networkX的所有graph生成器,下面的内容只是我节选的内容,并将graph画出来而已. 声明 ...

随机推荐

  1. 杭电2577 多数组dp问题

    Problem Description Pirates have finished developing the typing software. He called Cathy to test hi ...

  2. C#-Parallel

    using System; using System.Collections.Concurrent; using System.Collections.Generic; using System.Li ...

  3. C#倒计时关闭提示框

    前两天实现某个功能需要做一个提示框 并且能够自动关闭的,就从网上搜了一个能够自动关闭的提示框 ,但由于我需要的场景是不确定计时时间的,所以并没有使用到该窗体,但是我觉得可以留存备用 ,后边也把我 这种 ...

  4. 编写Postgres扩展之五：代码组织和版本控制

    原文:http://big-elephants.com/2015-11/writing-postgres-extensions-part-v/ 编译:Tacey Wong 在关于编写Postgres扩 ...

  5. 数据结构之链表(LinkedList)(一)

    链表(Linked List)介绍 链表是有序的列表,但是它在内存中是存储如下 1)链表是以节点方式存储的,是链式存储 2)每个节点包含data域(value),next域,指向下一个节点 3)各个节 ...

  6. 【转载】Asp.Net中Cookie对象的作用以及常见属性

    Cookie对象是服务器为用户访问存储的特定信息,这些信息一般存储在浏览器中,服务器可以从提交的数据中获取到相应的Cookie信息,Cookie的最大用途在于服务器对用户身份的确认,即票据认证,用户会 ...

  7. Hystrix原理与实战

    Hystrix原理与实战 背景 分布式系统环境下,服务间类似依赖非常常见,一个业务调用通常依赖多个基础服务. 比如:订单服务调用商品服务,商品服务调用库存服务. 对于同步调用,当库存服务不可用时,商品 ...

  8. 异常-Caused by: org.apache.hadoop.ipc.RemoteException(org.apache.hadoop.security.AccessControlException): Permission denied: user=hdfs, access=WRITE, inode="/hbase":root:supergroup:drwxr-xr-x

    1 详细异常 Caused by: org.apache.hadoop.ipc.RemoteException(org.apache.hadoop.security.AccessControlExce ...

  9. 这个在Github有52100颗星星的项目，怎么还有人不知道鸭！

    Ta是近两年Docker最为火热的开源项目之一.Docker 开启了容器时代,而Ta则革新了我们对于云计算,软件开发流程,业务平台等等方面的认知. Ta就是Kubernetes,/k(j)uːbəˈn ...

  10. 【年度盘点】10个热门Python练习项目

    这10个项目,约有270000人学习过. 今天给大家盘点一下实验楼最热门的10个Python练习项目.第二名是<200 行 Python 代码实现 2048>,第三名是<Python ...