P1352 没有上司的舞会&&树形DP入门

https://www.luogu.com.cn/problem/P1352

题目描述

某大学有N个职员，编号为1~N。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数Ri，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入格式

第一行一个整数N。(1<=N<=6000)

接下来N行，第i+1行表示i号职员的快乐指数Ri。(-128<=Ri<=127)

接下来N-1行，每行输入一对整数L,K。表示K是L的直接上司。

最后一行输入0 0

输出格式

输出最大的快乐指数。

输入输出样例

输入 #1复制

输出 #1复制

5样例分析：

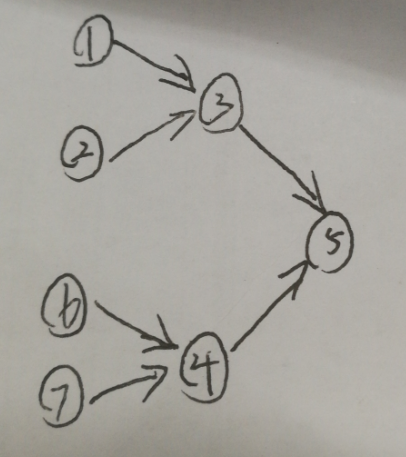
根节点为5，那么3，4不去，就可以获得最大快乐值=5

思路：可用树形DP或者拓扑排序来做一开始想到的可能是用一个一维数组dp[i]表示在第i个人的位置能获得的最大快乐，但是这个位置上的人去或者不去，都会对下属有影响，具有后效性，

比如说dp[2]作为根节点，那么他的最优解肯定是这个节点的快乐值，如果3要参加，则dp[3]无法继承dp[2]的最优解

那么我们可以在这个基础上增加一维，用来1/0表示这个人去还是不去如果不去，那么他的直接下属都可以去,dp[i][0]=sum((max(dp[son][1],dp[son][0])) son表示员工若去，则他的直接下属都不能去，dp[i][1]=sum(dp[son][0]);

那什么是后效性？

无后效性，有两层含义。

第一层含义是，在推导后面阶段状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步步推导出来的。

第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。

---来源CSDN博客

简单些的例子：迷宫问题中，假设你走到了(n,m)点，之后的状态转移不会再关心你是如何走到(n,m)点的，只关心你在(n,m)点的状态信息（例如耗费）。

之后发生的不会影响之前的结果。拿最长公共子序列来说，你在后面碰到的字符不会影响你前面字符的匹配数量和结果，每次增加匹配到的字符时，都是“继承”前面的结果之后加一。所以如果后面的字符如果能改变前面的字符，那么我们存状态意义就不大了。就是因为有大量重复计算在递归里，我们才用空间换时间，用了动态规划。如果状态总是变，那也没必要存了。每次都暴力算就行。---来源知乎某处（我忘了）

所以我们需要在这个基础上再加上一维，分别以0和1表示这个人去或者不去。

 #include<iostream>
 #include<cstring>
 #include<math.h>
 #include<stdlib.h>
 #include<cstring>
 #include<cstdio>
 #include<utility>
 #include<algorithm>
 #include<queue>
 using namespace std;
 typedef long long ll;
 inline int read(){
     ,w=;;
     while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
     )+(X<<)+(ch^),ch=getchar();
     return w?-X:X;
 }
 /*------------------------------------------------------------------------*/
 ;
 ],fa[maxn];
 vector<int>son[maxn];
 ;
 void bfs(int root){

     queue<int>q;
     q.push(root);
     vis[root]=;
     tree[++cnt]=root;

     while(!q.empty()){

         int now=q.front();q.pop();

         int len=son[now].size();

         ;i<len;++i){

             if(!vis[son[now][i]]){
                 vis[son[now][i]]=;
                 tree[++cnt]=son[now][i];
                 q.push(son[now][i]);
             }

         }

     }

 }
 int main( )
 {
     ios_base::sync_with_stdio(); cin.tie(); cout.tie();
     //freopen("a.txt","r",stdin);
     //freopen("a.txt","w",stdout);
     int n;
     cin>>n;
     ;i<n+;++i){
         fa[i]=i;
         cin>>v[i];

     }
     ;i<=n;++i){
         int u,v;
         cin>>u>>v;
         )break;

         fa[u]=v;
         son[v].push_back(u);

     }

     int root = n;

     while(fa[root]!=root)root=fa[root];

     bfs(root);

     //从叶子节点开始dp
     ;--i){

         int now=tree[i];
         int len=son[now].size();

         ;j<len;++j){//他的某一个下属 

             //1表示去
             dp[now][]+=max(dp[son[now][j]][],dp[son[now][j]][]);
             dp[now][]+=dp[son[now][j]][]; //如果now去，则now的下属不能去
         }

         dp[now][]+=v[now];
         //根节点，写在外面的原因是
         //叶子节点无法进入第二层循环
         //并且叶子节点表示now去，所以二维状态是1 

     }

     cout<<(max(dp[root][],dp[root][]))<<endl;

     ;
 }

拓扑排序的DP思想和上面的差不多，就是省略了建树的过程，因为拓扑排序的算法特殊性帮助我们完成了这一过程，根节点入度为0，那么我们就可以不断地在排序过程中完成DP

 #include<iostream>
 #include<cstring>
 #include<math.h>
 #include<stdlib.h>
 #include<cstring>
 #include<cstdio>
 #include<utility>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<map>
 using namespace std;
 ;
 ];
 int n;

 int main(){

     cin>>n;

     ;i<=n;++i){
         cin>>a[i];
     }
     vector<int>son[maxn];
     int u,v;
     while(cin>>u>>v&&u&&v){

         du[v]++;

         son[u].push_back(v);
     }

     queue<int>q;
     ;i<=n;++i){

         if(!du[i]){//叶子节点
             q.push(i);
             dp[i][]=a[i];
         }
     }
     map<int,int>mp;
     ;
     while(!q.empty()){

         int now=q.front();q.pop();
         int len=son[now].size();

         ;i<len;++i){

             int boss=son[now][i];
             dp[boss][]+=max(dp[now][],dp[now][]);
             dp[boss][]+=dp[now][];

             du[boss]--;
             if(!du[boss]){
                 dp[boss][]+=a[boss];
                 q.push(boss);
                 mp[i]=;
             }
             ans=max(dp[boss][],dp[boss][]);
         }

     }
     cout<<ans<<endl;
     ;
 }

发现我这个代码写的有点复杂。。。

参考了一位大佬的代码，和我的代码的区别是我用vector存每个节点的上司，那么判断过程中就需要每次从vector里面取出，其实我们只需要设置一个father数组用来存储就可以了

 #include<iostream>
 #include<cstring>
 #include<math.h>
 #include<stdlib.h>
 #include<cstring>
 #include<cstdio>
 #include<utility>
 #include<algorithm>
 #include<queue>
 using namespace std;
 typedef long long ll;
 inline int read(){
     ,w=;;
     while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
     )+(X<<)+(ch^),ch=getchar();
     return w?-X:X;
 }
 /*------------------------------------------------------------------------*/
 ;
 ],father[maxn],du[maxn];
 ;
 int main( )
 {
     ios_base::sync_with_stdio(); cin.tie(); cout.tie();
     //freopen("a.txt","r",stdin);
     //freopen("a.txt","w",stdout);

     int n;
     cin>>n;
     ;i<n+;++i){
         father[i]=i;
         cin>>v[i];

     }
     ;i<=n;++i){
         int u,v;
         cin>>u>>v;
         )break;

         father[u]=v;

         du[v]++;

     }
     queue<int>q;
     ;i<=n;++i){
         if(!du[i]){

             q.push(i);
         }

     }
     int root;
     while(!q.empty()){

         int now=q.front();q.pop();
         root=now;
         //上司不去
         dp[father[now]][]=max(dp[now][],dp[now][]);
         //去
         dp[father[now]][]+=v[father[now]]+dp[now][]; 

         du[father[now]]--;
         if(!du[father[now]]){
             q.push(father[now]);
         }
     }
     cout<<max(dp[root][],dp[root][])<<endl;

     ;
 }