RMQ问题总结，标准RMQ算法的实现

RMQ问题：对于长度为N的序列，询问区间[L,R]中的最值

RMQ问题的几种解法：

1. 普通遍历查询，O(1)-O(N)
2. 线段树，O(N)-O(logN)
3. DP，O(NlogN)-O(1)
4. RMQ标准算法，O(N)-O(1)

简单介绍：

1. 朴素的查询，不需要任何预处理，但结果是没有任何已知的信息可以利用，每次都需要从头遍历到尾。
2. 线段树，区间问题的神器，用线段树做比起朴素的暴力查询要快得多，关键在于线段树使用了分治思想，利用了区间问题的可合并性。任何一个区间最多只需要logN个线段树上的区间来合并，线段树上的区间总数目为O(N)个，因此只需要O(N)的预处理就可以将查询复杂度降到O(logN)。同时线段树的树状结构使得修改时信息更容易维护。
3. DP，又叫ST算法，也是利用了分治的思想。任何一个区间都可以由两个小于当前区间长度的最大的长度为2的幂的区间合并而来，于是预处理出每个点开始所有长度为2的幂的区间最值，那么查询时就可以由预处理的信息O(1)得到答案。
4. RMQ标准算法，利用了神奇的数据结构--笛卡尔树，笛卡尔树将区间最值问题转化为树上两个点的LCA问题，而DFS可以将LCA问题转化为±1RMQ问题，±1RMQ问题又可以利用分块和动态规划的思想来解决。上述所有预处理，包括笛卡尔树的建立、DFS序以及±1RMQ的问题的求解都可以在线性时间内完成，查询时复杂度为O(1)。

标准算法的实现：

• 结构图：
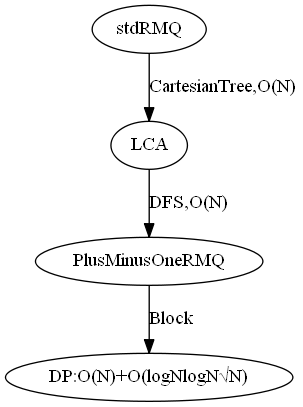
• 笛卡尔树的构造算方法：从左至右扫描原序列，并依次插入到笛卡尔树的右链中，使用单调栈复杂度为O(N)。建好树后，key是二查搜索树，value是小根堆。
• 最小值与LCA：建好树后，区间最小值问题便转化为了LCA问题，下面简单证明一下：

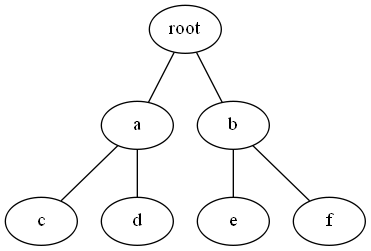
假设现在询问[d, f]的最小值，root为d和f的LCA，由笛卡尔树的性质可知，root是整棵树表示区间的最小值，而[d, f]是其子区间，所以root不可能比[d, f]中的数小，又因为d和f属于root的不同子树(LCA的性质)，所以root一定在[d, f]中(笛卡尔树的性质)，故对两个点a，b，LCA(a, b)就是[a, b]的最小值，证毕。

• ±1RMQ问题：相邻两个数相差1或者-1的序列的RMQ问题
• ±1RMQ问题解法：将原长度为N的序列分成2N/logN块，每块长度为logN/2，将原来的询问分解为块间询问和块内询问。用ST算法在O(N/logN*log(N/logN))=O(N)的时间内处理出块与块之间的区间最值信息，可以在O(1)的时间内解决块与块之间的询问。对于块内的询问，由于每块长度为logN/2，相邻两个数的差不是1就是-1，于是对于区间最值出现的位置，本质不同的状态只有2^logN/2=√N个，加上边界，总共状态数为O(√N*logNlogN)，利用递推在O(√N*logNlogN)的时间内求出所有状态来，以后可以在O(1)的时间内得到块内任意区间最值的位置。总复杂度为O(N + √N*logNlogN) ≈ O(N)。
• LCA与±1RMQ的经典转化就不细说了，详见代码

标准RMQ，O(N)-O(1)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148

struct PlusMinusOneRMQ { const static int N = ; const static int M = ; int blocklen, block, minv[N], dp[N][], t[N * ], f[ << M][M][M], s[N]; void init(int n) { blocklen = max(, (int)(log(n * 1.0) / log(2.0)) / ); block = n / blocklen + (n % blocklen > ); int total = << (blocklen - ); for (int i = ; i < total; i ++) { for (int l = ; l < blocklen; l ++) { f[i][l][l] = l; int now = , minv = ; for (int r = l + ; r < blocklen; r ++) { f[i][l][r] = f[i][l][r - ]; if (( << (r - )) & i) now ++; else { now --; if (now < minv) { minv = now; f[i][l][r] = r; } } } } } int tot = N * ; t[] = ; for (int i = ; i < tot; i ++) { t[i] = t[i - ]; if (!(i & (i - ))) t[i] ++; } } void initmin(int a[], int n) { for (int i = ; i < n; i ++) { if (i % blocklen == ) { minv[i / blocklen] = i; s[i / blocklen] = ; } else { if (a[i] < a[minv[i / blocklen]]) minv[i / blocklen] = i; if (a[i] > a[i - ]) s[i / blocklen] |= << (i % blocklen - ); } } for (int i = ; i < block; i ++) dp[i][] = minv[i]; for (int j = ; ( << j) <= block; j ++) { for (int i = ; i + ( << j) - < block; i ++) { int b1 = dp[i][j - ], b2 = dp[i + ( << (j - ))][j - ]; dp[i][j] = a[b1] < a[b2]? b1 : b2; } } } int querymin(int a[], int L, int R) { int idl = L / blocklen, idr = R / blocklen; if (idl == idr) return idl * blocklen + f[s[idl]][L % blocklen][R % blocklen]; else { int b1 = idl * blocklen + f[s[idl]][L % blocklen][blocklen - ]; int b2 = idr * blocklen + f[s[idr]][][R % blocklen]; int buf = a[b1] < a[b2]? b1 : b2; int c = t[idr - idl - ]; if (idr - idl - ) { int b1 = dp[idl + ][c]; int b2 = dp[idr - - ( << c) + ][c]; int b = a[b1] < a[b2]? b1 : b2; return a[buf] < a[b]? buf : b; } return buf; } } }; struct CartesianTree { private: struct Node { int key, value, l, r; Node(int key, int value) { this->key = key; this->value = value; l = r = ; } Node() {} }; Node tree[maxn]; int sz; int S[maxn], top; /** 小根堆 区间最小值*/ public: void build(int a[], int n) { top = ; tree[] = Node(-, 0x80000000);//将根的key和value赋为最小以保持树根不变 S[top ++] = ; sz = ; for (int i = ; i < n; i ++) { tree[++ sz] = Node(i, a[i]); int last = ; while (tree[S[top - ]].value >= tree[sz].value) { last = S[top - ]; top --; } tree[sz].l = last; tree[S[top - ]].r = sz; S[top ++] = sz; } } Node &operator [] (const int x) { return tree[x]; } };/** 树根为定值0，数组从0开始编号 **/ class stdRMQ { public: void work(int a[], int n) { ct.build(a, n); dfs_clock = ; dfs(, ); rmq.init(dfs_clock); rmq.initmin(depseq, dfs_clock); } int query(int L, int R) { int cl = clk[L], cr = clk[R]; if (cl > cr) swap(cl, cr); return value[rmq.querymin(depseq, cl, cr)]; } private: CartesianTree ct; PlusMinusOneRMQ rmq; int dfs_clock, clk[maxn], value[maxn << ], depseq[maxn << ]; void dfs(int rt, int d) { clk[ct[rt].key] = dfs_clock; depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; if (ct[rt].l) { dfs(ct[rt].l, d + ); depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; } if (ct[rt].r) { dfs(ct[rt].r, d + ); depseq[dfs_clock] = d; value[dfs_clock ++] = ct[rt].value; } } };