扩增|feather evolution
Wool vs feather
扩增方法:1.Gene Duplication2.Genome Duplication3.Cluster
哺乳动物毛发和鸟类的羽毛,都来自于角蛋白。
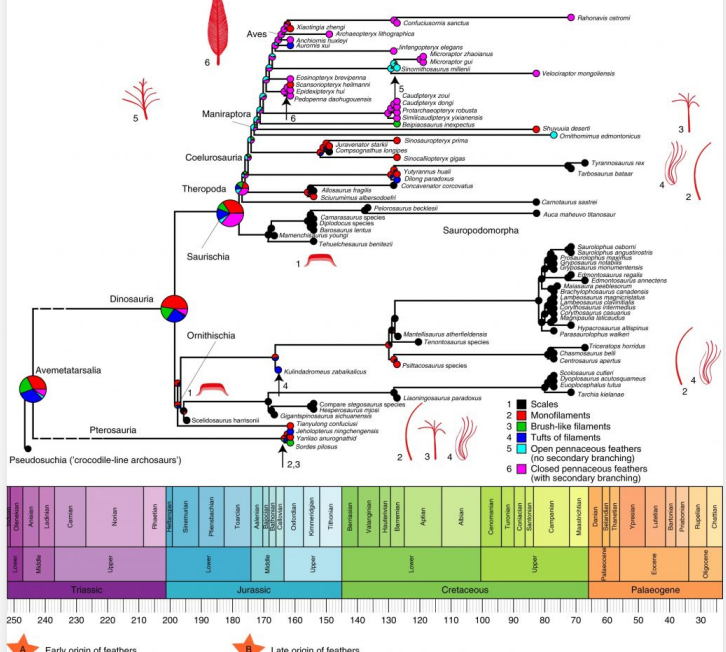
羽毛进化图
DNA水平修饰或RNA水平修饰处于二维。
细胞内的感觉受体可改变RNA序列。
扩增|feather evolution的更多相关文章
- 差分进化算法 DE-Differential Evolution
差分进化算法 (Differential Evolution) Differential Evolution(DE)是由Storn等人于1995年提出的,和其它演化算法一样,DE是一种模拟生物进化 ...
- Evolution项目(1)
Evolution项目是基于NFine修改的项目 主要改动为: 支持了.net core 1.0 支持了 EF core 1.0 支持数据库自动创建及Demo数据自动灌入 修改了授权方式 新增加了一个 ...
- 正则化方法:L1和L2 regularization、数据集扩增、dropout
正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合).其直观的表现如下图所示,随着训练过程的进行,模型复杂度增加,在tr ...
- ubuntu 14.04 下evolution邮箱客户端设置(腾讯企业邮箱)
安装 evolution 有PPA可用,支持 Ubuntu 14.04 及衍生系统.打开终端,输入以下命令: sudo add-apt-repository ppa:fta/gnome3 sudo a ...
- ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS
ON THE EVOLUTION OF MACHINE LEARNING: FROM LINEAR MODELS TO NEURAL NETWORKS We recently interviewed ...
- GFS: Evolution on Fast-forward
GFS: Evolution on Fast-forward by Marshall Kirk McKusick, Sean Quinlan | August 7, 2009 A discussion ...
- 长期演进技术(LTE,Long Term Evolution)
/********************************************************************************* * 长期演进技术(LTE,Long ...
- 正则化,数据集扩增,Dropout
正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合).其直观的表现如下图所示,随着训练过程的进行,模型复杂度增加,在tr ...
- UNIX Filesystems - Evolution Design and Implementation.pdf
UNIX Filesystems - Evolution Design and Implementation.pdf
随机推荐
- Centos下nginx安装
安装很简单,这里记录只是为了记下下载地址: A.[root@localhost soft]# wget http://nginx.org/download/nginx-1.4.2.tar.gz B.[ ...
- 循环(while,break,continue),转义字符
01. 程序的三大流程 在程序开发中,一共有三种流程方式: 顺序 -- 从上向下,顺序执行代码 分支 -- 根据条件判断,决定执行代码的 分支 循环 -- 让 特定代码 重复 执行 02. while ...
- multi-task learning
多任务学习, CTR, CVR 任务同时训练, 同时输出概率.
- PAT Advanced 1123 Is It a Complete AVL Tree (30) [AVL树]
题目 An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child ...
- UML-逻辑架构精化
向下请求:Facade模式 向上返回:观察者模式 不局限于上图中指定的层使用相应模式,其他层也可以使用. 另外,尽量不要出现“公共业务模块”,设计时尽量做好系统拆分.否则,一旦修改公共代码,可能会影响 ...
- CodeForces - 350B(反向建图,)
B - Resort CodeForces - 350B B. Resort time limit per test 2 seconds memory limit per test 256 megab ...
- 寒假day12
今天写了一点论文,刷了一些算法题
- 从编程实现角度学习Faster R-CNN(附极简实现)
https://www.jianshu.com/p/9da1f0756813 从编程实现角度学习Faster R-CNN(附极简实现) GoDeep 关注 2018.03.11 15:51* 字数 5 ...
- http head详解
Http普通报头: 少数报头域用于所有的请求和响应消息, 但并不用于被传输的实体 cache-Control: 用于指定缓存指令, 缓存指令是单向的 ,且是独立的(一个消息的缓存指令不会影 ...
- 吴裕雄--天生自然 JAVA开发学习:日期时间
import java.util.Date; public class DateDemo { public static void main(String args[]) { // 初始化 Date ...
