衡量线性回归法的指标MSE, RMSE,MAE和R Square
衡量线性回归法的指标:MSE, RMSE和MAE
举个栗子:
对于简单线性回归,目标是找到a,b 使得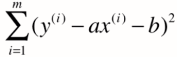 尽可能小
尽可能小
其实相当于是对训练数据集而言的,即
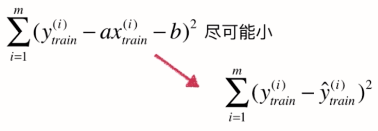
当我们找到a,b后,对于测试数据集而言
 ,理所当然,其衡量标准可以是
,理所当然,其衡量标准可以是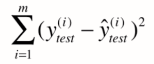
但问题是,这个衡量标准和m相关。
(当10000个样本误差累积是100,而1000个样本误差累积却达到了80,虽然80<100,但我们却不能说第二个模型优于第一个)
改进==> 对式子除以m,使得其与测试样本m无关
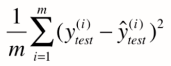 ->
-> 
但又有一个问题,之前算这个公式时为了保证其每项为正,且可导(所以没用绝对值的表示方法),我们对式子加了一个平方。但这可能会导致量纲的问题,如房子价格为万元,平方后就成了万元的平方。
又改进==> 对MSE开方,使量纲相同
 ->
->
MSE与RMSE的区别仅在于对量纲是否敏感
又一思路,通过加绝对值
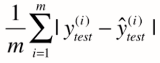 ->
-> 
在推导a,b的式子时(对train数据集),没用求绝对值的方法是因为其不是处处可导,不方便用来求极值。但评价模型时,对test数据集我们完全可以使用求绝对值的方式。
P.S. 评价模型的标准和训练模型时最优化的目标函数是可以完全不一样的。
RMSE vs MAE
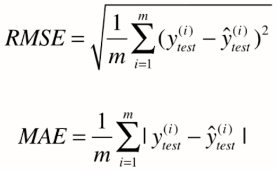
RMSE 与 MAE 的量纲相同,但求出结果后我们会发现RMSE比MAE的要大一些。
这是因为RMSE是先对误差进行平方的累加后再开方,它其实是放大了较大误差之间的差距。
而MAE反应的就是真实误差。因此在衡量中使RMSE的值越小其意义越大,因为它的值能反映其最大误差也是比较小的。
衡量线性回归法最好的指标 R Squared
对于上述的衡量方法,如RMSE和MAE还是有问题的,还是因为量纲不一样。比如我们预测考试分数误差是10,预测房价误差是1w。但我们却不能评价我们的模型是更适合预测分数还是预测房价。
解决方法==> 新的指标:R方
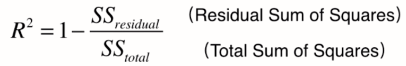
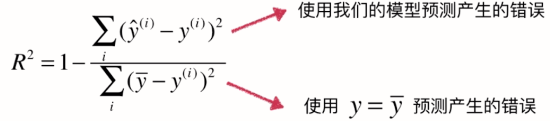
(上:y预测-y真,our model,下:y真平均-y真,baseline model)
使用baseline模型肯定会产生很多错误,我们自己的模型产生的错误会少一些。
1 - ourModelError / baselineModelError = 我们模型拟合住的部分

R方将回归结果归约到了0~1间,允许我们对不同问题的预测结果进行比对了。

我们可发现,上面其实就是MSE,下面就是方差
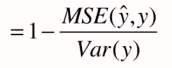
衡量线性回归法的指标MSE, RMSE,MAE和R Square的更多相关文章
- 【笔记】衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square
衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square 衡量线性回归法的指标 对于分类问题来说,我们将原始数据分成了训练数据集和测试数据集两部分,我们使用训练数据集得到模型以后 ...
- 机器学习:衡量线性回归法的指标(MSE、RMSE、MAE、R Squared)
一.MSE.RMSE.MAE 思路:测试数据集中的点,距离模型的平均距离越小,该模型越精确 # 注:使用平均距离,而不是所有测试样本的距离和,因为距离和受样本数量的影响 1)公式: MSE:均方误差 ...
- 可决系数R^2和MSE,MAE,SMSE
波士顿房价预测 首先这个问题非常好其实要完整的回答这个问题很有难度,我也没有找到一个完整叙述这个东西的资料,所以下面主要是结合我自己的理解和一些资料谈一下r^2,mean square error 和 ...
- 第3章 衡量线性回归的指标:MSE,RMSE,MAE
, , ,, , , ,
- 线性回归中常见的一些统计学术语(RSE RSS TSS ESS MSE RMSE R2 Pearson's r)
TSS: Total Sum of Squares(总离差平方和) --- 因变量的方差 RSS: Residual Sum of Squares (残差平方和) --- 由误差导致的真实值和估计值 ...
- SSE,MSE,RMSE,R-square指标讲解
SSE(和方差.误差平方和):The sum of squares due to errorMSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...
- SSE,MSE,RMSE,R-square 指标讲解
SSE(和方差.误差平方和):The sum of squares due to error MSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...
- Data Mining: SSE,MSE,RMSE,R-square指标讲解
转载自:http://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差.误差平方和):The sum of squares due ...
- C / C ++ 基于梯度下降法的线性回归法(适用于机器学习)
写在前面的话: 在第一学期做项目的时候用到过相应的知识,觉得挺有趣的,就记录整理了下来,基于C/C++语言 原贴地址:https://helloacm.com/cc-linear-regression ...
随机推荐
- mysql 忘记root密码的解决办法
1.修改MySQL的登录设置: # vim /etc/my.cnf 在[mysqld]的段中加上一句:skip-grant-tables 例如: [mysqld] datadir=/var/lib/m ...
- MySQL查询优化方法总结
1.应尽量避免在 where 子句中使用!=或<>操作符,否则将引擎放弃使用索引而进行全表扫描. 2.对查询进行优化,应尽量避免全表扫描,首先应考虑在 where 及 order by 涉 ...
- java uuid第一次性能
在java中产生uuid的方式是使用java.util.UUID. UUID.randomUUID().toString(); 我在测试redis性能时,使用uuid产生测试数据,发现多线程测试red ...
- Linux下解压ZIP压缩包乱码问题
并不是所有ZIP文件都是乱码的而且导致解压失败,只有windows下压缩的ZIP在Linux中会出现这种情况.这是因为Windows和Linux下用的字符编码不同.Windows下的编码格式为GBK, ...
- Spoj REPEATS 后缀自动机+set
REPEATS - Repeats 链接:http://www.spoj.com/problems/REPEATS 题意:求S串中某个子串连续循环次数最多的次数. 想法: 从暴力开始,枚举所有串,求出 ...
- 在Linux系统里安装Virtual Box的详细步骤
今天我试图在Linux 服务器上安装Kyma时,遇到如下错误消息: E1009 23:51:37.685891 358 start.go:174] Error starting host: Error ...
- JAVA小基础
JAVA的jsp程序中,jar如果不能再引用的时候加入到lib文件夹而选择外部引用,可能会导致jar不能被找到的问题. string.format的占位符一般使用%s表示字符串的意思,与C#的{0}这 ...
- redis的一些问题总结,转载自infoq
Redis是时下比较流行的Nosql技术.在优酷我们使用Redis Cluster构建了一套内存存储系统,项目代号蓝鲸.到目前为止集群有700+节点,即将达到作者推荐的最大集群规模1000节点.集群从 ...
- 解决nginx bind() to 0.0.0.0:80 failed 问题
nginx的配置文件一开始默认是80端口,出现这个错误多半是80端口已经被占用.这时候只需要把 server { listen 8088; server_name localhost lcsf.com ...
- IOS CoreData 多表查询(下)
http://blog.csdn.net/fengsh998/article/details/8123392 在iOS CoreData中,多表查询上相对来说,没有SQL直观,但COREDATA的功能 ...
