题解 P3374 【【模板】树状数组 1】

恩，这是AC的第一道树状数组呢。

本蒟蒻以前遇到RMQ问题一般都用线段树或ST表，可惜ST表不支持在线修改，而线段树代码量又太大。

如今终于找到了折中方案：树状数组！！！！
代码量小，还支持修改！

---

树状数组也就是二叉索引树，又被称为Fenwick树，然而我个人认为它不能被严谨地成为树，因为充其量只是借用的树形结构的思想，于实现上有着较大的区别。

树状数组虽然运用范围没有线段树那么广，但是它的效率要高很多，比如线段树是$nlogn$，但树状数组是$logn$。

还有一点需要注意的是：树状数组可以区间查询，但不能运用于任意区间查询。这一点在后面会提到。

---

那么这个树状数组的基本思路就是

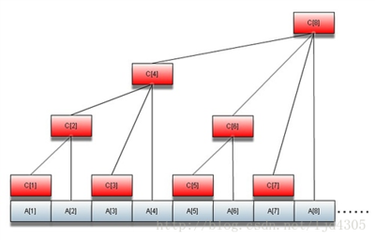
用节点ci储存和，比如：

- c1=a1
- c2=a1+a2
- c3=a3
- c4=a1+a2+a3+a4
- c5=a5
- c6=a5+a6
- c7=a7
- c8=a1+...+a8

当然这样子可能不是很容易看出内在的联系，因此不妨将其转化为二进制来观察：

- c0001=a0001
- c0010=a0001+a0010
- c0011=a0011
- c0100=a0001+a0010+a0011+a0100
- c0101=a0101
- c0110=a0101+a0110
- c0111=a0111
- c1000=a0001+...+a1000

是不是发现了什么？

没有吗？好吧。

事实上这里的规律就是cn=a(n–2^k+1)+...+an，这里的k指的是n二进制末尾0的数量。

获取2^k的操作我们称之为lowbit，其实现如下：

int lowbit(int k){
    return k&(-k);
}

有了lowbit操作之后，求和就很好写了：

 int query(int x){
     int ans=;
     while(x!=){
         ans+=tree[x];
         x-=lowbit(x);
     }
     return ans;
 }

要注意一点，这里求的ans是区间[1,x]的和，想要[y,x]的和只能$query(x)-query(y-1)$。

因此我们回到了之前那个问题：树状数组不能解决所有区间查询，它只能解决如上的有关联的区间查询。

emmmm.....还有update操作：

 void update(int x,int k){
     while(x<=n){
         tree[x]+=k;
         x+=lowbit(x);
     }
 }

这个在明白了树状数组的本质之后也很好理解，就不多做叙述了。

---

总的来说，树状数组挺好用的，值得一学。但切记，无论如何都必须掌握线段树，因为能用树状数组解决的都能用线段树，而反之不一定如此。

另附AC代码见下：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 using namespace std;

 const int maxn=;

 int n,m;
 int tree[maxn<<];

 int lowbit(int k){
     return k&(-k);
 }

 void update(int x,int k){
     while(x<=n){
         tree[x]+=k;
         x+=lowbit(x);
     }
 }

 int query(int x){
     int ans=;
     while(x!=){
         ans+=tree[x];
         x-=lowbit(x);
     }
     return ans;
 }

 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++){
         int a;
         scanf("%d",&a);
         update(i,a);
     }
     for(int i=;i<=m;i++){
         int a,b,c;
         scanf("%d%d%d",&a,&b,&c);
         if(a==)update(b,c);
         else printf("%d\n",query(c)-query(b-));
     }
 }