Manacher 求最长回文子串算法

Manacher算法，是由一个叫Manacher的人在1975年发明的，可以在$O(n)$的时间复杂度里求出一个字符串中的最长回文子串。

例如这两个回文串“level”、“noon”，Manacher算法先对其进行一个处理：

level    -->  #l#e#v#e#l#

noon    -->    #n#o#o#n#

这样的好处就是，不论回文子串的长度是奇是偶，最后求出的回文子串长度都是奇数的，就不用分类讨论了。

我们用p[i]表示以i为中心的最长回文子串向两边扩展的长度，例如：

s     #  1  #  2  #  2  #  1   #  2  #  3  #  2  #  1  #
    p     1  2  1  2  5  2  1  4   1  2  1  6  1  2  1  2  1

我们发现，p[i]-1刚好为原串以i位置为中心的最长回文子串长度。

在Manacher算法中，需要两个辅助变量。id为当前最长回文子串的中心，mx为以id为中心的最长回文子串的右边界（id+p[id]）。这个算法的核心部分在这里：

if(mx>i)p[i]=min(p[(id<<1)-i],mx-i);else p[i]=1;

当 mx - i > p[j] 的时候，以s[j]为中心的回文子串包含在以s[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 p[i] = p[j]。

当 p[j] > mx - i 的时候，以s[j]为中心的回文子串不完全包含于以s[id]为中心的回文子串中，但是由于对称性，以s[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 p[i] >= mx - i。至于mx之后的部分是否对称，就只能一个一个匹配了。

当 mx  < i 的时候，我们就无法对 p[i] 进行更多的推算，只能一个一个匹配。

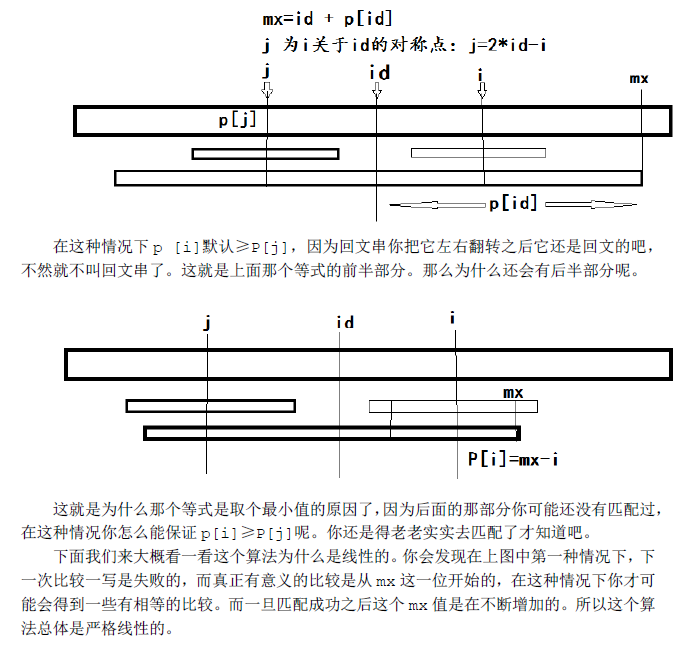
上图给出了Manacher的详解和线性复杂度的证明。

以下是核心代码：

C++ Code：

void manacher(){
	int mx=0,id=0;
	for(i=1;i<=n;++i){
		if(mx>i)p[i]=min(p[(id<<1)-i],mx-i);else p[i]=1;
		while(s[i-p[i]]==s[i+p[i]])++p[i];
		if(i+p[i]>mx)mx=i+p[id=i];
	}
}