CMOD实施了一个增强，但是不需要了，怎么删除呢？

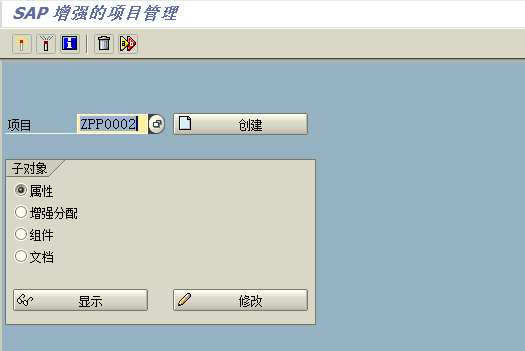
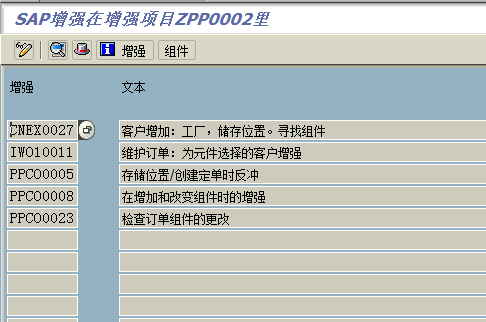
要删除PPCO0005 这个增强，进入编辑状态，发现没有删除按钮，  把PPCO0005 这项删除掉

敲回车，厉害了，他又回来了，所以在这里是没法删除的；

那么，回到CMOD 初始界面 先取消激活

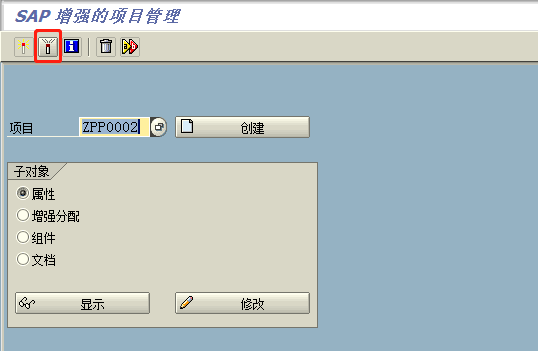
再修改增强分配，就有了删除按钮

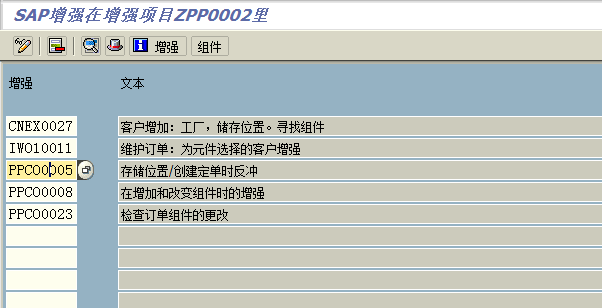
临时发现要删的是 IWO10011 这个组件，删除，保存再激活项目就好了

增强篇6 CMOD增强删除的更多相关文章

  1. SAP 增强篇 Method1 BADI增强的查找方法

    查找BADI的方法:(1)通过SE24,输入CL_EXITHANDLER,然后在方法GET_INSTANCE中设置断点,然后运行事务代码判断 exit_name的值,操作过程如下:输入se24,然后输 ...

  2. SAP翔子_增强篇索引

    序号 描述 SAP翔子_增强篇0 增强篇0 SAP的多种增强方式 SAP翔子_增强篇1 增强篇1 PO保存增强 SAP翔子_增强篇2 增强篇2 生产订单屏幕增强 SAP翔子_增强篇3 增强篇3 SAP ...

  3. SAP增强总结-第二代增强（SMOD、CMOD）【转载】

    第二代增强比第二代增强安全性提高了很多,第一代增强毕竟是在原标准程序中修改,大部分传递参数都可以直接使用,第二代增强做了一些封装,对用户可以修改的参数做了限制. 1.增强点查找方法 首先根据事物码找到 ...

  4. AI佳作解读系列(四)——数据增强篇

    前言 在深度学习的应用过程中,数据的重要性不言而喻.继上篇介绍了数据合成(个人认为其在某种程度上可被看成一种数据增强方法)这个主题后,本篇聚焦于数据增强来介绍几篇杰作! (1)NanoNets : H ...

  5. ES6学习一 JS语言增强篇

    一 背景 JavaScript经过二十来年年的发展,由最初简单的交互脚本语言,发展到今天的富客户端交互,后端服务器处理,跨平台(Native),以及小程序等等的应用.JS的角色越来越重要,处理场景越来 ...

  6. SAP增强 和VA01相关增强点介绍

    -转 sap寻找用户出口方法 sap的用户出口总共有三代: 一.User EXIT 第一代的用户出口,它们include在SAP标准程序的源代码里,可以说他们是源代码的一部分,你改了这种出口就相当于改 ...

  7. 基于Selenium的Web自动化框架增强篇

    在写完上一篇“基于Selenium的Web自动化框架”(http://www.cnblogs.com/AlwinXu/p/5836709.html)之后一直没有时间重新审视该框架,正好趁着给同事分享的 ...

  8. 增强篇4 CO01生产订单屏幕增强

    Step1. 结构 CO_AUFK 里增加自定义字段:ZZZ_TRIAL 然后激活结构 查看AUFK是激活状态, 字段增强完成: Step2. CMOD  使用客户增强:PPCO0012    生产订 ...

  9. C#的变迁史 - C# 5.0 之其他增强篇

    1. 内置zip压缩与解压 Zip是最为常用的文件压缩格式之一,也被几乎所有操作系统支持.在之前,使用程序去进行zip压缩和解压要靠第三方组件去支持,这一点在.NET4.5中已有所改观,Zip压缩和解 ...

随机推荐

  1. goto语句——慎用，但是可以用

    最近使用了goto语句,是因为if嵌套太深了,因此把错误处理同意了,直接使用goto语句. 举例: #include <stdio.h> int main () { /* local va ...

  2. SPOJ - BALNUM - Balanced Numbers（数位DP）

    链接: https://vjudge.net/problem/SPOJ-BALNUM 题意: Balanced numbers have been used by mathematicians for ...

  3. Hive节点及原理

    1.什么是Hive:hive是一种基于hadoop的数据仓库,能够将结构化的数据映射成一张表,并提供HQL进行查询.其数据是存储在hdfs上,本质是将sql命令转化成MapReduce来执行. 2.H ...

  4. [GCP] Goolge compute Engine

    Which of the following is a PAAS option for hosting web apps on GCP? App Engine standard or flexible ...

  5. LeetCode 311. Sparse Matrix Multiplication

    原题链接在这里:https://leetcode.com/problems/sparse-matrix-multiplication/description/ 题目: Given two sparse ...

  6. Linux 一条长命令占用多行

    前言 考察下面的脚本: ? 1 emcc -o ./dist/test.html --shell-file ./tmp.html --source-map-base dist -O3 -g4 --so ...

  7. Postgresql 进程和内存结构

    在本章中,总结了PostgreSQL中的流程体系结构和内存体系结构,以帮助阅读后续章节.如果您已经熟悉它们,可以跳过本章 1.进程结构 Postgresql 是一个C/S架构的关系型数据库,由多个后台 ...

  8. Deepgreen & Greenplum DBA小白普及课之三

    Deepgreen & Greenplum DBA小白普及课之三(备份问题解答) 不积跬步无以至千里,要想成为一名合格的数据库管理员,首先应该具备扎实的基础知识及问题处理能力.本文参考Pivo ...

  9. sql server vs mysql

    1.中文: my.ini [mysqld] character-set-server=utf8 character-set-client=utf8 data\testdb\db.opt default ...

  10. regedit系统注册表，msconfig系统配置

    msconfig msconfig即系统配置实用程序,是Microsoft System Configuration的缩写.是在开始菜单里运行中输入然后确认就可以找到程序开启或者禁用, 可以帮助电脑禁 ...