洛谷 题解 P1041 【传染病控制】

【思路】

题目给出一棵树。第\(i\)步拆的一定是第\(i\)层与第\(i+1\)层之间的连边，否则不是最优（自行证明即可），所以可以暴力枚举每一次拆哪一个节点与上一个节点的连边。

把所有节点所在的层数存下来，一号点在第\(1\)层，枚举每一层的每个节点（由于\(1\)号节点已经被感染，从第二层开始搜索就可以了）

大概可分为以下几步：

• 存好一整棵树

• 把每一层的节点都存在一个数组里面

• 标记以ii号节点为根节点的子树的节点个数

• 标记与回溯

• 暴力搜索

【细节精讲】

1、树的存储

关于多叉树的存储，这里介绍一种简单有效的方法。考虑如下代码：

struct Node
{
	int father;
	int child[MAXN];
}tree[MAXN];

\(tree[i]\)存\(i\)号节点的所有信息：

\(father\)存父亲(在这题没有用) ； \(child[]\)存它所有的孩子 ； \(child[0]\)是它孩子的个数。

由于数据范围很小，我们不用担心造成空间过多的浪费。

结构体构建完成之后，我们就可以在读入的同时把整棵树存好。

n=read();p=read();
for(int i=1;i<=p;i++)
{
	int x=read(),y=read();
	if(x>y)swap(x,y);
	tree[y].father=x;
	tree[x].child[++tree[x].child[0]]=y;
}

2 、标记深度

如果能够理解，标记深度是比较简单的。

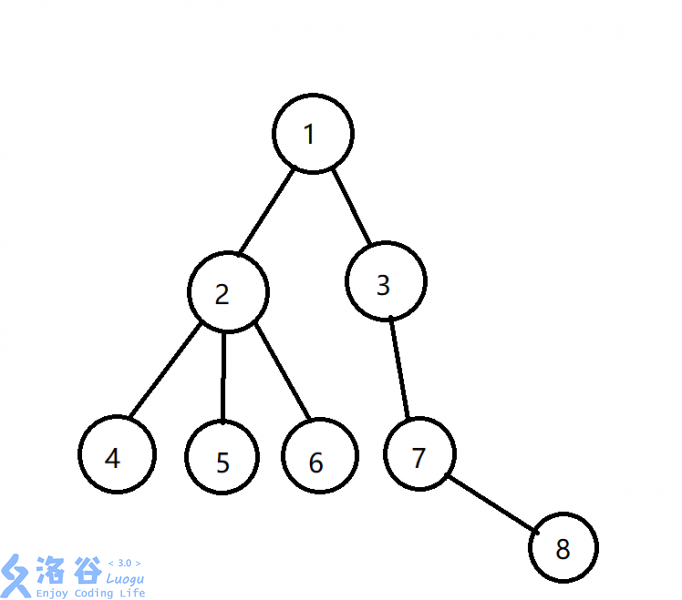
如图：我们令\(1\)号节点的深度为\(1\) ； 则\(2,3\)节点深度为\(2\) ； \(4,5,6,7\)节点的深度为\(3\)； \(8\)节点的深度为\(4\)。这棵树一共有\(4\)层。

代码用\(deep[i][j]\)存第\(i\)层第\(j\)个节点的编号。\(deep[i][0]\)是第\(i\)层一共的节点数。

inline void getdeep(int now,int Nowdeep)//当前的节点标号是now，层数是Nowdeep
{
	maxdeep=max(maxdeep,Nowdeep);//标记一共有几层
	for(int i=1;i<=tree[now].child[0];i++)
	{
		deep[Nowdeep][++deep[Nowdeep][0]]=tree[now].child[i];//把这个节点放到第i层的数组中
		getdeep(tree[now].child[i],Nowdeep+1);//以这个点为父节点继续标记它的儿子。每个节点的深度等于它父节点的深度+1
	}
}

3、切断问题

我们知道，只要一个点与上层点的传播途径被切断，即这个点不会得传染病，那么以这个点为根节点的整个子树都应该被标记为安全。

这一段代码用来标记\(now\)这个节点为根节点的子树一共有多少节点，存在\(num[]\)中。

inline int getnum(int now)
{
	for(int i=1;i<=tree[now].child[0];i++)
		num[now]+=getnum(tree[now].child[i]);
	return num[now];
}

4、回溯

接下来，我们切断了这个节点，相应地，以这个点为根节点的子树都应该被标记。（\(tag=1\)表示标记，\(tag=0\)表示删去标记，用于回溯）

inline void work(int now,bool tag)
{
	vis[now]=tag;
	for(int i=1;i<=tree[now].child[0];i++)
	{
		vis[tree[now].child[i]]=tag;
		work(tree[now].child[i],tag);
	}
}

5、搜索

做完上面这些铺垫操作之后，我们可以开始整个代码的核心：搜索了。

首先可以想到如下代码

inline void DFS(int now,int cnt)
{
	if((now==maxdeep))
	{
		ans=min(ans,cnt);
		return;
	}
	for(int i=1;i<=deep[now][0];i++)
	{
		if(vis[deep[now][i]])
			continue;
		work(deep[now][i],1);
		DFS(now+1,cnt-num[deep[now][i]]);
		work(deep[now][i],0);
	}
}

但是提交这段代码的话只能得80分。为什么呢？

我们可以考虑这样一棵树：

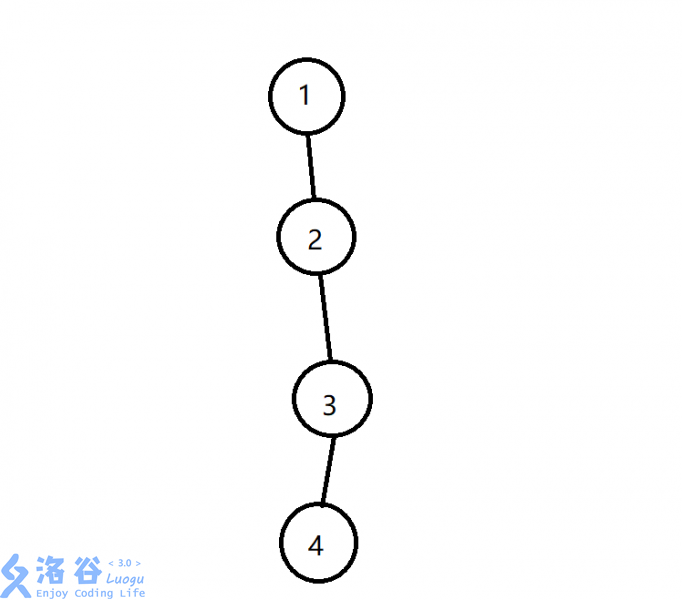
它是一条链。我们第一次只能切断1号节点和2号节点之间的连边，这样第三层所有的节点就都被标记了。那么问题是什么呢？根本就搜不到最后一层的节点，导致答案根本没有更新！

于是我们优化一下搜索代码：

inline void DFS(int now,int cnt)
{
	int tot=0;//记录总数
	if((now==maxdeep))
	{
		ans=min(ans,cnt);
		return;
	}
	for(int i=1;i<=deep[now][0];i++)
	{
		if(vis[deep[now][i]])
		{
			tot++;
			continue;
		}
		work(deep[now][i],1);
		DFS(now+1,cnt-num[deep[now][i]]);
		work(deep[now][i],0);
	}
	if(tot==deep[now][0])//如果全部都被访问过了，那么直接更新答案
		ans=min(ans,cnt);
}

【代码】

#include<bits/stdc++.h>
using namespace std;
const int MAXN=300+10;
int n,p;
struct Node
{
	int father;
	int child[MAXN];
}tree[MAXN];
int num[MAXN];
int deep[MAXN][MAXN];
int maxdeep=0;
bool vis[MAXN];
int ans=0x3f3f3f3f;
inline int read()
{
	int tot=0;
	char c=getchar();
	while(c<'0'||c>'9')
		c=getchar();
	while(c>='0'&&c<='9')
	{
		tot=(tot<<1)+(tot<<3)+c-'0';
		c=getchar();
	}
	return tot;
}
inline void getdeep(int now,int Nowdeep)
{
	maxdeep=max(maxdeep,Nowdeep);
	for(int i=1;i<=tree[now].child[0];i++)
	{
		deep[Nowdeep][++deep[Nowdeep][0]]=tree[now].child[i];
		getdeep(tree[now].child[i],Nowdeep+1);
	}
}
inline int getnum(int now)
{
	for(int i=1;i<=tree[now].child[0];i++)
		num[now]+=getnum(tree[now].child[i]);
	return num[now];
}
inline void work(int now,bool tag)
{
	vis[now]=tag;
	for(int i=1;i<=tree[now].child[0];i++)
	{
		vis[tree[now].child[i]]=tag;
		work(tree[now].child[i],tag);
	}
}
inline void DFS(int now,int cnt)
{
	int tot=0;
	if((now==maxdeep))
	{
		ans=min(ans,cnt);
		return;
	}
	for(int i=1;i<=deep[now][0];i++)
	{
		if(vis[deep[now][i]])
		{
			tot++;
			continue;
		}
		work(deep[now][i],1);
		DFS(now+1,cnt-num[deep[now][i]]);
		work(deep[now][i],0);
	}
	if(tot==deep[now][0])
		ans=min(ans,cnt);
}
int main()
{
	n=read();p=read();
	fill(num+1,num+1+n,1);
	for(int i=1;i<=p;i++)
	{
		int x=read(),y=read();
		if(x>y)swap(x,y);
		tree[y].father=x;
		tree[x].child[++tree[x].child[0]]=y;
	}
	/*for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=tree[i].child[0];i++)cout<<tree[i].child[j]<<" ";
		cout<<endl;
	}*/
	getdeep(1,2);
	/*for(int i=2;i<=maxdeep;i++)
	{
		for(int j=1;j<=deep[i][0];j++)cout<<deep[i][j]<<" ";
		cout<<endl;
	}*/
	getnum(1);
	DFS(2,n);
	printf("%d\n",ans);
	return 0;
}

\[\color{red}\large\text{完结撒花}
\]

参考博客