ireport初接触

我用的版本5.6.0

@官网下载地址

下载安装@参考博客龙凌云端，着重留意：在windows下使用，只下载iReport-5.6.0-windows-installer.exe就行了

安装后配置环境变量@参考博客龙凌云端，着重留意：修改iReport-5.6.0\etc 目录下的配置文件 ireport.conf，修改jdkhome="C:\Program Files\Java\jdk1.7.0_75"

java使用所需要的jar包@参考博客孙公

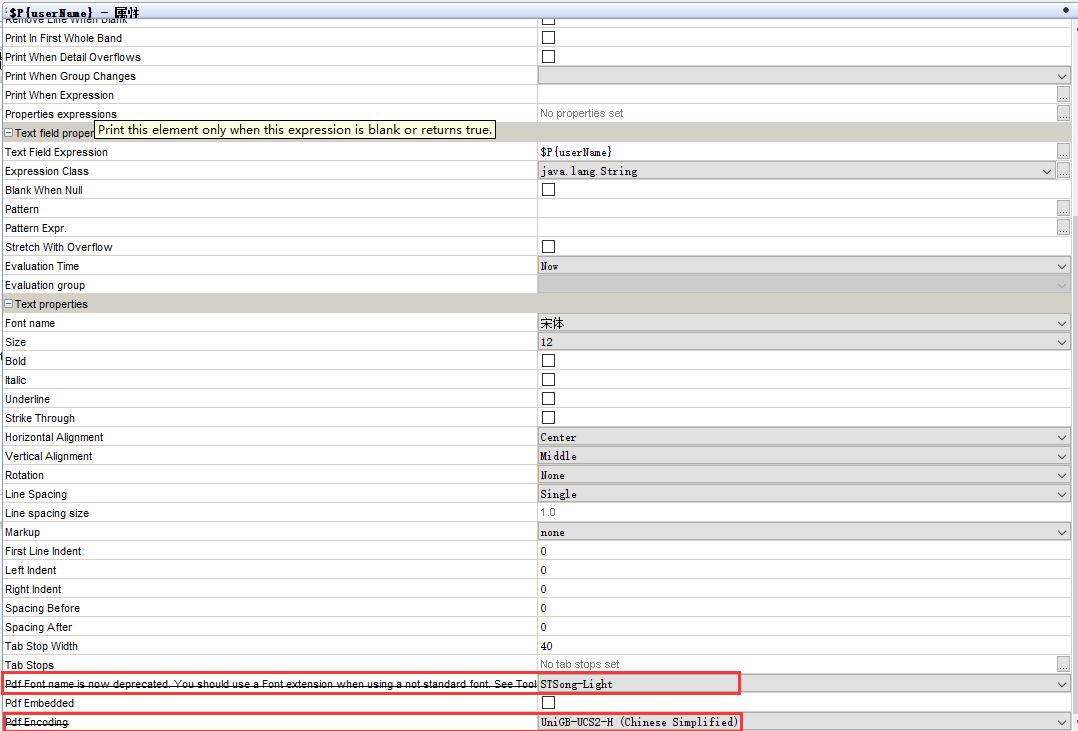
java传参中文不显示问题，看了一些博客没找到适合我的解决方案，最后自己发现进行如下设置就好了

list组件拉上去就不能编译，总是报异常

 net.sf.jasperreports.engine.design.JRValidationException: Report design not valid :       
　　1. List contents width must be positive.

网上找了近一天也没找到解决方案，最后查看源码发现<jr:listContents height="50" width="0"/>，没错，新拉的list组件width为0，我把width改为正数就好了。我真应该早点看源码。。。也奉劝读到这里的读者碰到类似问题也多看看源码吧。

list使用方式：

右击Parameters——添加Parameter，改名，改类型为list或collection

拖拽list组件到需要的位置，左侧会自动生成dataset和List(component)

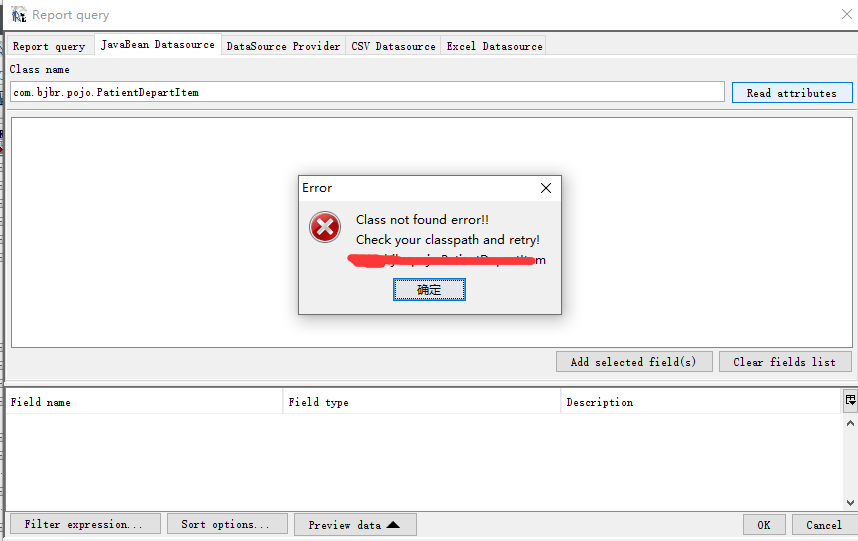
然后给dataset1的fields添加属性，可以手动添加，也可右击dataset1——edit Query，JavaBean Datasource，将classname的完整 Qualified Name粘贴，然后Read Attributes，选中需要添加的属性，Add selected fields，ok

当选择javabean datasource时，需提前设置class文件夹，工具——选项ireport——classpath把项目的class文件夹添加进来

然后list组件右键 edit datasource，connection/datasource exp将jremptydatasource中的值改为你的$P{你的list名

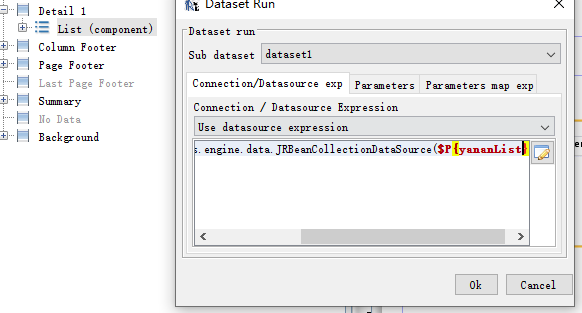
着重留意：new net.sf.jasperreports.engine.data.JRBeanCollectionDataSource($P{yananList})，

new net.sf.jasperreports.engine.data.JRBeanCollectionDataSource别写猜错了

然后向list框中从dataset的fields中拖入属性即可

20191209@各区块作用：

报表的结构：

各块区域------

Title----报表名，只在第一页显示

pageHeader-----放页码，时间，创建人，每一页都会显示出来

columnHeader-----列名

detail----循环的数据，比如说我们直接从数据库中得到数据，只用将字段拖到此区域，那么就会将所有的这个字段的值进行循环了。

-----需要注意的是：table中因为放了数据，也会将这些数据接着循环。到头来，本来一个table已经将数据给循环完了，但是又由于detail的循环性质，将整个table又循环了。所以table是不能放在detail中的。这回循环table。

columnFooter-----与columnHeader相反，可以用来统计此列数据。

pageFooter-------每页底部都会显示的，如页码

lastPageFooter----最后一页的底部，如日期，签名.....

Summary--------可能需要对几页（你的报表可能有几个页组成）的统计值。比如50个销售记录共占用了3页，那么放置这些统计记录的统计值最好的地方就是summary。     Summary只在最后一页出现。