『7.5 NOIP模拟赛题解』

<更新提示>

<正文>

T1 Gift

Description

人生赢家老王在网上认识了一个妹纸,然后妹纸的生日到了，为了表示自己的心意，他决定送她礼物。可是她喜爱的东西特别多，然而他的钱数有限，因此他想知道当他花一定钱数后剩余钱数无法再购买任何一件剩余物品(每种物品他最多买一个)时有多少种方案，两种方案不同，当且仅当两种方案中至少有一件品不同，可是由于他忙着准备泡下一个妹纸(chi)，因此麻烦聪明的你帮帮忙。

Input Format

输入第一行 n 和 m， n 表示妹纸喜欢的礼物数目， m 表示现有的钱数，第二行 n 个数，表示 n 个物品的价格。

Output Format

输出一行一个数表示方案数目，答案对 1000000007 取模。

Sample Input

6 25

8 9 8 7 16 5

Sample Output

Hint

30%的数据: 0<=n<=100 0<=m<=500

100%的数据:0<=n<=1000 0<=m<=1000

注意：所有物品价格均小于 m

解析

如果存在一种合法的方案，就必然会有一个未购买并且价格最低的物品，并且这种方案的情况下，已经没有足够的钱来购买这个物品了。那么我们就以这个未购买的最小价格物品为基准点来统计答案，保证不重不漏。

我们先将所有物品按照价格从小到大排序，每次枚举一个物品\(i\)，令这个物品作为上述未购买且价格最低的物品，然后，我们强制取第\(1\)到\(i-1\)个物品(如果不取，就和\(i\)个物品最小矛盾)，并对第\(i+1\)到\(n\)个物品用\(0/1\)背包统计方案数，那么\(\sum_{j\in [m-a[i]+1,m]}f[j]\)即为本次的答案。

我们发现每一次\(dp\)都是对后面连续的若干个物品进行计算，于是我们就可以放弃背包中滚动数组的做法，从\(n\)开始倒序\(dp\)，并记录每一个阶段的\(dp\)值，然后在上述统计答案的过程中直接使用预处理的\(dp\)值即可。这样，时间复杂度就从\(O(n^3)\)优化到了\(O(n^2)\)。

\(Code:\)

#include <bits/stdc++.h>

using namespace std;

const int N = 1020 , M = 1020;

const long long Mod = 1000000007;

int n,m,a[N];

long long f[N][M],ans,sum[N];

inline void input(void)

{

	scanf("%d%d",&n,&m);

	for (int i=1;i<=n;i++)

		scanf("%d",&a[i]);

}

inline void dp(void)

{

	memset( f , 0 , sizeof f );

	f[n+1][0] = 1;

	for (int i=n;i>=1;i--)

		for (int j=0;j<=m;j++)

			if ( j >= a[i] ) f[i][j] = ( f[i+1][j] + f[i+1][j-a[i]] ) % Mod;

			else f[i][j] = f[i+1][j];

	for (int k=1;k<=n;k++)

	{

		for (int i=m;i>=sum[k-1];i--)

			f[k+1][i] = f[k+1][i-sum[k-1]];

		for (int i=0;i<min(sum[k-1],1LL*m+1);i++)

			f[k+1][i] = 0;

		for (int i=m;i>=m-a[k]+1;i--)

			ans = ( ans + f[k+1][i] ) % Mod;

	}

}

int main(void)

{

	input();

	sort( a+1 , a+n+1 );

	for (int i=1;i<=n;i++)

		sum[i] = sum[i-1] + a[i];

	dp();

	if ( sum[n] > m ) printf("%lld\n",ans%Mod);

	else puts("1");

	return 0;

}

T2 Fseq

Description

一个长度为 N+M 的数列，里面有 N 个+1,M 个-1 如果一个这样的数列被称作 F 序列(Fadeness) ，当且仅当它的任意前缀和均非负。

for example :

1,-1,1,1,-1 is a Fadeness

1,-1,-1,1,1 is not because S(3) <0

求一个数列是 Fadensee 的概率。

Input Format

第一行， Test , 表示测试数据的组数。每个数据有两个数 N,M

Output Format

对于每组数据,输出一个实数（保留到小数点后 6 位）

Sample Input

Sample Output

Hint

30%的数据： (Test<=10)，(0<=N,M<=1000).

100%的数据： ( Test<=9008 )， ( 0<=N,M<=20000 ).

解析

和选举定理相似，我们直接转换成图形问题，然后应用反射原理即可。

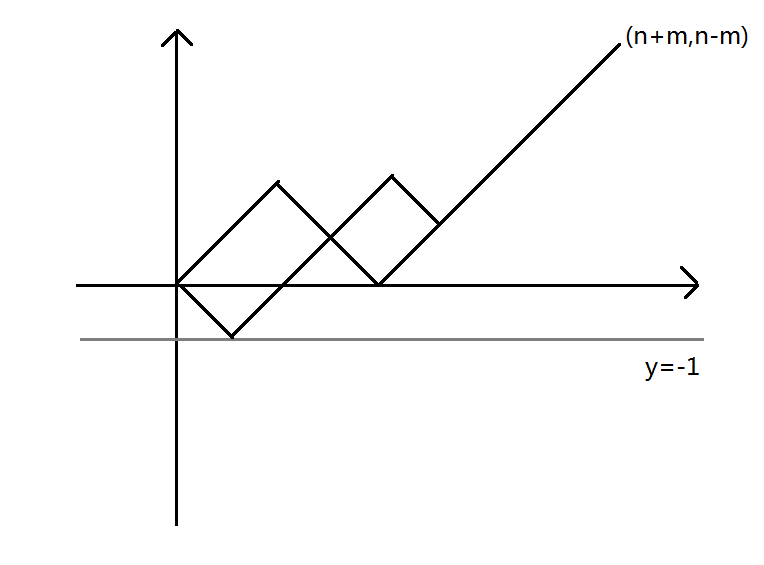
我们将数列取数形象地转化为坐标系中的移动问题，一开始在原点，每取一个\(1\)就向右上方走一步，横纵坐标各加\(1\)，取一个\(-1\)就向右下方走一步，横坐标加\(1\)，纵坐标减\(1\)，那么最终折线会走到点\((n+m,n-m)\)。

那么一旦折线接触到了直线\(y=-1\)，这个序列就是不合法的。容易得出折线共有\(C_{n+m}^m\)种，那么问题在于求出不合法的折线数。

应用反射原理，由点\((0,-2)\)为起点，向右上走\(n+1\)次，向右下走\(m-1\)次，最终到点\((n+m,n-m)\)的所有折线就是不合法的折线数，我们同样可以得出这样的折线有\(C_{n+m}^{m-1}\)种。

那么答案就是\(\frac{C_{n+m}^m-C_{n+m}^{m-1}}{C_{n+m}^m}\)，化简一下就是\(1-\frac{m}{n+1}\)。

\(Code:\)

#include<bits/stdc++.h>

using namespace std;

const int T = 10020 , N = 20020;

int t,n,m;

int main(void)

{

	scanf("%d",&t);

	while ( t-- )

	{

		scanf("%d%d",&n,&m);

		if ( m > n ) puts("0.000000");

		else printf("%.6lf\n", 1.0 - 1.0 * m / (n+1) );

	}

	return 0;

}

<后记>