2015ACM/ICPC亚洲区长春站 B hdu 5528 Count a * b

Count a * b

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 211    Accepted Submission(s): 116

Problem Description

Marry likes to count the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0.

Let's denote f(m) as the number of ways to choose two non-negative integers a and b less than m to make a×b mod m≠0.

She has calculated a lot of f(m) for different m, and now she is interested in another function g(n)=∑m|nf(m). For example, g(6)=f(1)+f(2)+f(3)+f(6)=0+1+4+21=26. She needs you to double check the answer.

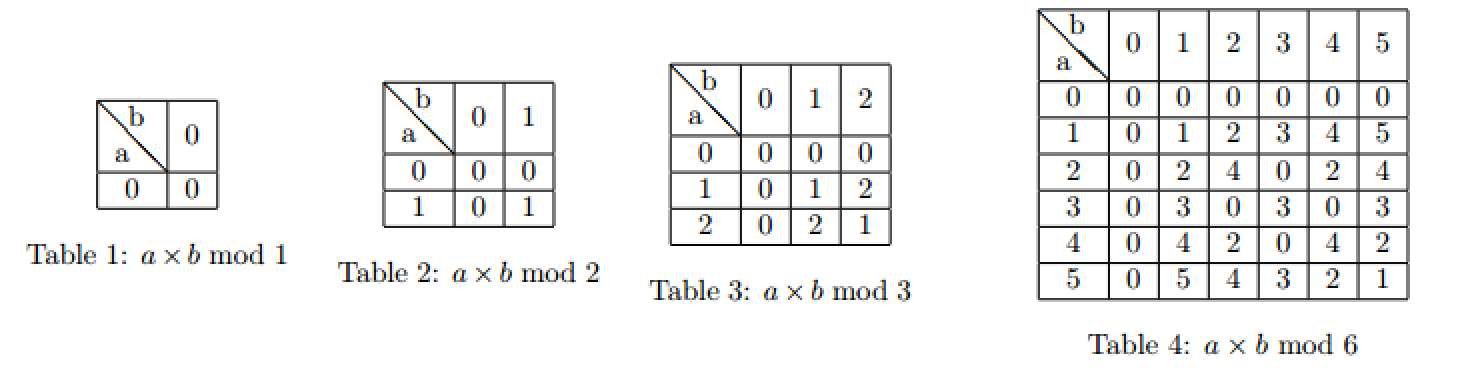
Give you n. Your task is to find g(n) modulo 264.

 

Input

The first line contains an integer T indicating the total number of test cases. Each test case is a line with a positive integer n.

1≤T≤20000
1≤n≤109

 

Output

For each test case, print one integer s, representing g(n) modulo 264.

 

Sample Input

2
6
514

 

Sample Output

26
328194

 

Source

2015ACM/ICPC亚洲区长春站-重现赛（感谢东北师大）

 

题意：略

分析：http://blog.csdn.net/firstlucker/article/details/49336427

这篇题解不错。

下面说明:x的约数的欧拉函数的和 = x

即sigma(d|x, phi(d)) = x

因为对于所有1-x的数，与x的gcd必定为x的约数，设为d，那这样的数有多少？phi(x / d)个

又发现x/d也是x的约数，所以。。。

sigma(d|x, phi(d)) = sigma(d|x, phi(x/d)) = x

这篇题解最后一步用了约数和定理。

 

其代码中防溢出运算更是简单、机智的令人发指

 

 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <cmath>
 #include <ctime>
 #include <iostream>
 #include <map>
 #include <set>
 #include <algorithm>
 #include <vector>
 #include <deque>
 #include <queue>
 #include <stack>
 using namespace std;
 typedef long long LL;
 typedef double DB;
 #define MIT (2147483647)
 #define MLL (1000000000000000001LL)
 #define INF (1000000001)
 #define For(i, s, t) for(int i = (s); i <= (t); i ++)
 #define Ford(i, s, t) for(int i = (s); i >= (t); i --)
 #define Rep(i, n) for(int i = (0); i < (n); i ++)
 #define Repn(i, n) for(int i = (n)-1; i >= (0); i --)
 #define mk make_pair
 #define ft first
 #define sd second
 #define puf push_front
 #define pub push_back
 #define pof pop_front
 #define pob pop_back
 #define sz(x) ((int) (x).size())
 #define clr(x, y) (memset(x, y, sizeof(x)))
 inline void SetIO(string Name)
 {
     string Input = Name + ".in";
     string Output = Name + ".out";
     freopen(Input.c_str(), "r", stdin);
     freopen(Output.c_str(), "w", stdout);
 }

 inline int Getint()
 {
     char ch = ' ';
     int Ret = ;
     bool Flag = ;
     while(!(ch >= '' && ch <= ''))
     {
         if(ch == '-') Flag ^= ;
         ch = getchar();
     }
     while(ch >= '' && ch <= '')
     {
         Ret = Ret *  + ch - '';
         ch = getchar();
     }
     return Ret;
 }

 const int N = ;
 int n;
 int Prime[N], Tot;
 bool Visit[N];

 inline void GetPrime()
 {
     For(i, , N-)
     {
         if(!Visit[i]) Prime[++Tot] = i;
         For(j, , Tot)
         {
             if(i * Prime[j] >= N) break;
             Visit[i * Prime[j]] = ;
             if(!(i % Prime[j])) break;
         }
     }
 }

 inline void Solve();

 inline void Input()
 {
     GetPrime();
     int TestNumber = Getint();
     while(TestNumber--)
     {
         n = Getint();
         Solve();
     }
 }

 inline void Solve()
 {
     if(n == )
     {
         puts("");
         return;
     }

     LL Total = , Except = n;
     For(i, , Tot)
     {
         if(Prime[i] * Prime[i] > n) break;
         if(!(n % Prime[i]))
         {
             int Fact = ;
             LL Cnt = ;
             while(!(n % Prime[i]))
             {
                 Cnt *= Prime[i];
                 Fact++;
                 n /= Prime[i];
             }
             Except *= Fact;
             Cnt *= Prime[i];
             LL a = (Cnt - ) / (Prime[i] - ), b = Cnt + , c = Prime[i] + ;
             Total *= ((a / c) * (b / c) * c + a % c * (b / c) + b % c * (a / c));
             //cout << Total << ' ' << Except << endl;
         }
     }

     if(n > ) Except <<= , Total *= ( + 1LL * n * n);
     cout << Total - Except << endl;
 }

 int main()
 {
     SetIO("");
     Input();
     //Solve();
     return ;
 }