伸展树(二)之 C++的实现
概要
上一章介绍了伸展树的基本概念，并通过C语言实现了伸展树。本章是伸展树的C++实现，后续再给出Java版本。还是那句老话，它们的原理都一样，择其一了解即可。
目录
1. 伸展树的介绍
2. 伸展树的C++实现(完整源码)
3. 伸展树的C++测试程序
转载请注明出处：http://www.cnblogs.com/skywang12345/p/3604258.html
更多内容: 数据结构与算法系列 目录
(01) 伸展树(一)之 图文解析 和 C语言的实现
(02) 伸展树(二)之 C++的实现
(03) 伸展树(三)之 Java的实现
伸展树的介绍
伸展树(Splay Tree)是特殊的二叉查找树。
它的特殊是指，它除了本身是棵二叉查找树之外，它还具备一个特点: 当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。
伸展树的C++实现
1. 基本定义
1.1 节点
template <class T>
class SplayTreeNode{
public:
T key; // 关键字(键值)
SplayTreeNode *left; // 左孩子
SplayTreeNode *right; // 右孩子 SplayTreeNode():left(NULL),right(NULL) {} SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r):
key(value), left(l),right(r) {}
};
SplayTreeNode是伸展树节点对应的类。它包括的几个组成元素:
(01) key -- 是关键字，是用来对伸展树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
1.2 伸展树
template <class T>
class SplayTree {
private:
SplayTreeNode<T> *mRoot; // 根结点 public:
SplayTree();
~SplayTree(); // 前序遍历"伸展树"
void preOrder();
// 中序遍历"伸展树"
void inOrder();
// 后序遍历"伸展树"
void postOrder(); // (递归实现)查找"伸展树"中键值为key的节点
SplayTreeNode<T>* search(T key);
// (非递归实现)查找"伸展树"中键值为key的节点
SplayTreeNode<T>* iterativeSearch(T key); // 查找最小结点：返回最小结点的键值。
T minimum();
// 查找最大结点：返回最大结点的键值。
T maximum(); // 旋转key对应的节点为根节点，并返回值为根节点。
void splay(T key); // 将结点(key为节点键值)插入到伸展树中
void insert(T key); // 删除结点(key为节点键值)
void remove(T key); // 销毁伸展树
void destroy(); // 打印伸展树
void print();
private: // 前序遍历"伸展树"
void preOrder(SplayTreeNode<T>* tree) const;
// 中序遍历"伸展树"
void inOrder(SplayTreeNode<T>* tree) const;
// 后序遍历"伸展树"
void postOrder(SplayTreeNode<T>* tree) const; // (递归实现)查找"伸展树x"中键值为key的节点
SplayTreeNode<T>* search(SplayTreeNode<T>* x, T key) const;
// (非递归实现)查找"伸展树x"中键值为key的节点
SplayTreeNode<T>* iterativeSearch(SplayTreeNode<T>* x, T key) const; // 查找最小结点：返回tree为根结点的伸展树的最小结点。
SplayTreeNode<T>* minimum(SplayTreeNode<T>* tree);
// 查找最大结点：返回tree为根结点的伸展树的最大结点。
SplayTreeNode<T>* maximum(SplayTreeNode<T>* tree); // 旋转key对应的节点为根节点，并返回值为根节点。
SplayTreeNode<T>* splay(SplayTreeNode<T>* tree, T key); // 将结点(z)插入到伸展树(tree)中
SplayTreeNode<T>* insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z); // 删除伸展树(tree)中的结点(键值为key)，并返回被删除的结点
SplayTreeNode<T>* remove(SplayTreeNode<T>* &tree, T key); // 销毁伸展树
void destroy(SplayTreeNode<T>* &tree); // 打印伸展树
void print(SplayTreeNode<T>* tree, T key, int direction);
};
SplayTree是伸展树对应的类。它包括根节点mRoot和伸展树的函数接口。
2. 旋转
旋转是伸展树中需要重点关注的，它的代码如下：
/*
* 旋转key对应的节点为根节点，并返回值为根节点。
*
* 注意：
* (a)：伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
* b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
* (c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
* c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::splay(SplayTreeNode<T>* tree, T key)
{
SplayTreeNode<T> N, *l, *r, *c; if (tree == NULL)
return tree; N.left = N.right = NULL;
l = r = &N; for (;;)
{
if (key < tree->key)
{
if (tree->left == NULL)
break;
if (key < tree->left->key)
{
c = tree->left; /* rotate right */
tree->left = c->right;
c->right = tree;
tree = c;
if (tree->left == NULL)
break;
}
r->left = tree; /* link right */
r = tree;
tree = tree->left;
}
else if (key > tree->key)
{
if (tree->right == NULL)
break;
if (key > tree->right->key)
{
c = tree->right; /* rotate left */
tree->right = c->left;
c->left = tree;
tree = c;
if (tree->right == NULL)
break;
}
l->right = tree; /* link left */
l = tree;
tree = tree->right;
}
else
{
break;
}
} l->right = tree->left; /* assemble */
r->left = tree->right;
tree->left = N.right;
tree->right = N.left; return tree;
} template <class T>
void SplayTree<T>::splay(T key)
{
mRoot = splay(mRoot, key);
}
上面的代码的作用：将"键值为key的节点"旋转为根节点，并返回根节点。它的处理情况共包括：
(a)：伸展树中存在"键值为key的节点"。
将"键值为key的节点"旋转为根节点。
(b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
b-1) "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
b-2) "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
(c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
c-1) "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
c-2) "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
下面列举个例子分别对a进行说明。
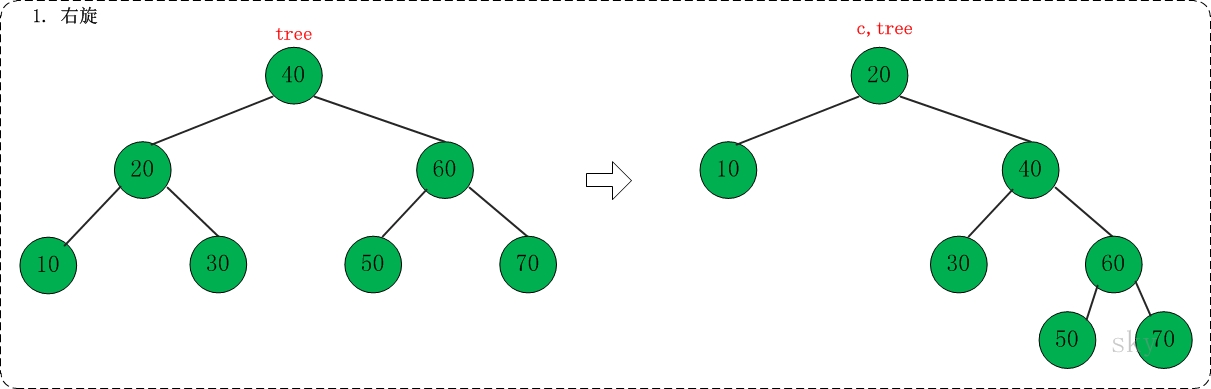
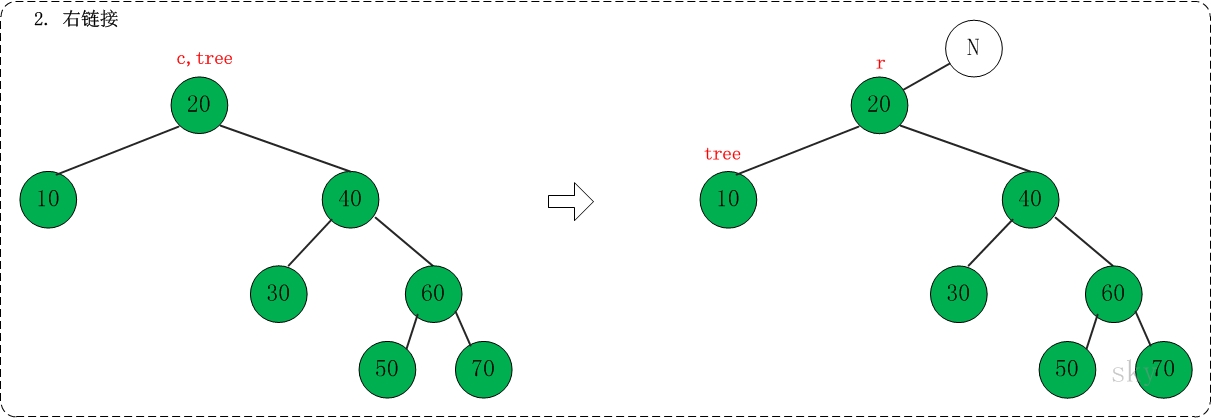
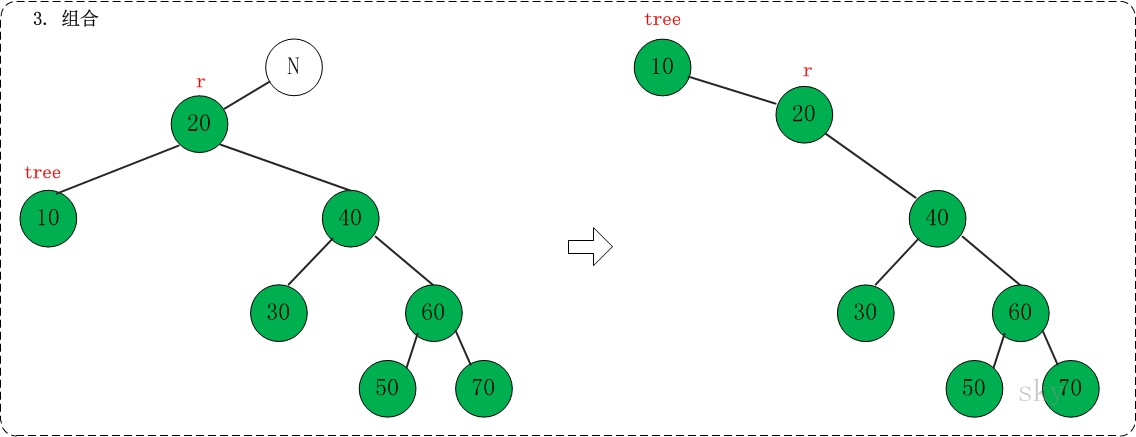
在下面的伸展树中查找10，共包括"右旋" --> "右链接" --> "组合"这3步。
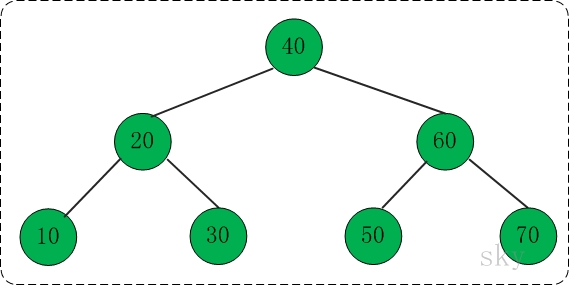
(01) 右旋
对应代码中的"rotate right"部分
(02) 右链接
对应代码中的"link right"部分
(03) 组合
对应代码中的"assemble"部分
提示：如果在上面的伸展树中查找"70"，则正好与"示例1"对称，而对应的操作则分别是"rotate left", "link left"和"assemble"。
其它的情况，例如"查找15是b-1的情况，查找5是b-2的情况"等等，这些都比较简单，大家可以自己分析。
3. 插入
插入代码
/*
* 将结点插入到伸展树中，并返回根节点
*
* 参数说明：
* tree 伸展树的根结点
* key 插入的结点的键值
* 返回值：
* 根节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z)
{
SplayTreeNode<T> *y = NULL;
SplayTreeNode<T> *x = tree; // 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key < x->key)
x = x->left;
else if (z->key > x->key)
x = x->right;
else
{
cout << "不允许插入相同节点(" << z->key << ")!" << endl;
delete z;
return tree;
}
} if (y==NULL)
tree = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z; return tree;
} template <class T>
void SplayTree<T>::insert(T key)
{
SplayTreeNode<T> *z=NULL; // 如果新建结点失败，则返回。
if ((z=new SplayTreeNode<T>(key,NULL,NULL)) == NULL)
return ; // 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
}
insert(key)是提供给外部的接口，它的作用是新建节点(节点的键值为key)，并将节点插入到伸展树中；然后，将该节点旋转为根节点。
insert(tree, z)是内部接口，它的作用是将节点z插入到tree中。insert(tree, z)在将z插入到tree中时，仅仅只将tree当作是一棵二叉查找树，而且不允许插入相同节点。
4. 删除
删除代码
/*
* 删除结点(节点的键值为key)，返回根节点
*
* 参数说明：
* tree 伸展树的根结点
* key 待删除结点的键值
* 返回值：
* 根节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::remove(SplayTreeNode<T>* &tree, T key)
{
SplayTreeNode<T> *x; if (tree == NULL)
return NULL; // 查找键值为key的节点，找不到的话直接返回。
if (search(tree, key) == NULL)
return tree; // 将key对应的节点旋转为根节点。
tree = splay(tree, key); if (tree->left != NULL)
{
// 将"tree的前驱节点"旋转为根节点
x = splay(tree->left, key);
// 移除tree节点
x->right = tree->right;
}
else
x = tree->right; delete tree; return x; } template <class T>
void SplayTree<T>::remove(T key)
{
mRoot = remove(mRoot, key);
}
remove(key)是外部接口，remove(tree, key)是内部接口。
remove(tree, key)的作用是：删除伸展树中键值为key的节点。
它会先在伸展树中查找键值为key的节点。若没有找到的话，则直接返回。若找到的话，则将该节点旋转为根节点，然后再删除该节点。
注意：关于伸展树的"前序遍历"、"中序遍历"、"后序遍历"、"最大值"、"最小值"、"查找"、"打印"、"销毁"等接口与"二叉查找树"基本一样，这些操作在"二叉查找树"中已经介绍过了，这里就不再单独介绍了。当然，后文给出的伸展树的完整源码中，有给出这些API的实现代码。这些接口很简单，Please RTFSC(Read The Fucking Source Code)！
伸展树的C++实现(完整源码)
伸展树的实现文件(SplayTree.h)
#ifndef _SPLAY_TREE_HPP_
#define _SPLAY_TREE_HPP_ #include <iomanip>
#include <iostream>
using namespace std; template <class T>
class SplayTreeNode{
public:
T key; // 关键字(键值)
SplayTreeNode *left; // 左孩子
SplayTreeNode *right; // 右孩子 SplayTreeNode():left(NULL),right(NULL) {} SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r):
key(value), left(l),right(r) {}
}; template <class T>
class SplayTree {
private:
SplayTreeNode<T> *mRoot; // 根结点 public:
SplayTree();
~SplayTree(); // 前序遍历"伸展树"
void preOrder();
// 中序遍历"伸展树"
void inOrder();
// 后序遍历"伸展树"
void postOrder(); // (递归实现)查找"伸展树"中键值为key的节点
SplayTreeNode<T>* search(T key);
// (非递归实现)查找"伸展树"中键值为key的节点
SplayTreeNode<T>* iterativeSearch(T key); // 查找最小结点：返回最小结点的键值。
T minimum();
// 查找最大结点：返回最大结点的键值。
T maximum(); // 旋转key对应的节点为根节点，并返回值为根节点。
void splay(T key); // 将结点(key为节点键值)插入到伸展树中
void insert(T key); // 删除结点(key为节点键值)
void remove(T key); // 销毁伸展树
void destroy(); // 打印伸展树
void print();
private: // 前序遍历"伸展树"
void preOrder(SplayTreeNode<T>* tree) const;
// 中序遍历"伸展树"
void inOrder(SplayTreeNode<T>* tree) const;
// 后序遍历"伸展树"
void postOrder(SplayTreeNode<T>* tree) const; // (递归实现)查找"伸展树x"中键值为key的节点
SplayTreeNode<T>* search(SplayTreeNode<T>* x, T key) const;
// (非递归实现)查找"伸展树x"中键值为key的节点
SplayTreeNode<T>* iterativeSearch(SplayTreeNode<T>* x, T key) const; // 查找最小结点：返回tree为根结点的伸展树的最小结点。
SplayTreeNode<T>* minimum(SplayTreeNode<T>* tree);
// 查找最大结点：返回tree为根结点的伸展树的最大结点。
SplayTreeNode<T>* maximum(SplayTreeNode<T>* tree); // 旋转key对应的节点为根节点，并返回值为根节点。
SplayTreeNode<T>* splay(SplayTreeNode<T>* tree, T key); // 将结点(z)插入到伸展树(tree)中
SplayTreeNode<T>* insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z); // 删除伸展树(tree)中的结点(键值为key)，并返回被删除的结点
SplayTreeNode<T>* remove(SplayTreeNode<T>* &tree, T key); // 销毁伸展树
void destroy(SplayTreeNode<T>* &tree); // 打印伸展树
void print(SplayTreeNode<T>* tree, T key, int direction);
}; /*
* 构造函数
*/
template <class T>
SplayTree<T>::SplayTree():mRoot(NULL)
{
} /*
* 析构函数
*/
template <class T>
SplayTree<T>::~SplayTree()
{
destroy(mRoot);
} /*
* 前序遍历"伸展树"
*/
template <class T>
void SplayTree<T>::preOrder(SplayTreeNode<T>* tree) const
{
if(tree != NULL)
{
cout<< tree->key << " " ;
preOrder(tree->left);
preOrder(tree->right);
}
} template <class T>
void SplayTree<T>::preOrder()
{
preOrder(mRoot);
} /*
* 中序遍历"伸展树"
*/
template <class T>
void SplayTree<T>::inOrder(SplayTreeNode<T>* tree) const
{
if(tree != NULL)
{
inOrder(tree->left);
cout<< tree->key << " " ;
inOrder(tree->right);
}
} template <class T>
void SplayTree<T>::inOrder()
{
inOrder(mRoot);
} /*
* 后序遍历"伸展树"
*/
template <class T>
void SplayTree<T>::postOrder(SplayTreeNode<T>* tree) const
{
if(tree != NULL)
{
postOrder(tree->left);
postOrder(tree->right);
cout<< tree->key << " " ;
}
} template <class T>
void SplayTree<T>::postOrder()
{
postOrder(mRoot);
} /*
* (递归实现)查找"伸展树x"中键值为key的节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::search(SplayTreeNode<T>* x, T key) const
{
if (x==NULL || x->key==key)
return x; if (key < x->key)
return search(x->left, key);
else
return search(x->right, key);
} template <class T>
SplayTreeNode<T>* SplayTree<T>::search(T key)
{
return search(mRoot, key);
} /*
* (非递归实现)查找"伸展树x"中键值为key的节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::iterativeSearch(SplayTreeNode<T>* x, T key) const
{
while ((x!=NULL) && (x->key!=key))
{
if (key < x->key)
x = x->left;
else
x = x->right;
} return x;
} template <class T>
SplayTreeNode<T>* SplayTree<T>::iterativeSearch(T key)
{
return iterativeSearch(mRoot, key);
} /*
* 查找最小结点：返回tree为根结点的伸展树的最小结点。
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::minimum(SplayTreeNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->left != NULL)
tree = tree->left;
return tree;
} template <class T>
T SplayTree<T>::minimum()
{
SplayTreeNode<T> *p = minimum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
} /*
* 查找最大结点：返回tree为根结点的伸展树的最大结点。
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::maximum(SplayTreeNode<T>* tree)
{
if (tree == NULL)
return NULL; while(tree->right != NULL)
tree = tree->right;
return tree;
} template <class T>
T SplayTree<T>::maximum()
{
SplayTreeNode<T> *p = maximum(mRoot);
if (p != NULL)
return p->key; return (T)NULL;
} /*
* 旋转key对应的节点为根节点，并返回值为根节点。
*
* 注意：
* (a)：伸展树中存在"键值为key的节点"。
* 将"键值为key的节点"旋转为根节点。
* (b)：伸展树中不存在"键值为key的节点"，并且key < tree->key。
* b-1 "键值为key的节点"的前驱节点存在的话，将"键值为key的节点"的前驱节点旋转为根节点。
* b-2 "键值为key的节点"的前驱节点存在的话，则意味着，key比树中任何键值都小，那么此时，将最小节点旋转为根节点。
* (c)：伸展树中不存在"键值为key的节点"，并且key > tree->key。
* c-1 "键值为key的节点"的后继节点存在的话，将"键值为key的节点"的后继节点旋转为根节点。
* c-2 "键值为key的节点"的后继节点不存在的话，则意味着，key比树中任何键值都大，那么此时，将最大节点旋转为根节点。
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::splay(SplayTreeNode<T>* tree, T key)
{
SplayTreeNode<T> N, *l, *r, *c; if (tree == NULL)
return tree; N.left = N.right = NULL;
l = r = &N; for (;;)
{
if (key < tree->key)
{
if (tree->left == NULL)
break;
if (key < tree->left->key)
{
c = tree->left; /* rotate right */
tree->left = c->right;
c->right = tree;
tree = c;
if (tree->left == NULL)
break;
}
r->left = tree; /* link right */
r = tree;
tree = tree->left;
}
else if (key > tree->key)
{
if (tree->right == NULL)
break;
if (key > tree->right->key)
{
c = tree->right; /* rotate left */
tree->right = c->left;
c->left = tree;
tree = c;
if (tree->right == NULL)
break;
}
l->right = tree; /* link left */
l = tree;
tree = tree->right;
}
else
{
break;
}
} l->right = tree->left; /* assemble */
r->left = tree->right;
tree->left = N.right;
tree->right = N.left; return tree;
} template <class T>
void SplayTree<T>::splay(T key)
{
mRoot = splay(mRoot, key);
} /*
* 将结点插入到伸展树中，并返回根节点
*
* 参数说明：
* tree 伸展树的根结点
* key 插入的结点的键值
* 返回值：
* 根节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::insert(SplayTreeNode<T>* &tree, SplayTreeNode<T>* z)
{
SplayTreeNode<T> *y = NULL;
SplayTreeNode<T> *x = tree; // 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key < x->key)
x = x->left;
else if (z->key > x->key)
x = x->right;
else
{
cout << "不允许插入相同节点(" << z->key << ")!" << endl;
delete z;
return tree;
}
} if (y==NULL)
tree = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z; return tree;
} template <class T>
void SplayTree<T>::insert(T key)
{
SplayTreeNode<T> *z=NULL; // 如果新建结点失败，则返回。
if ((z=new SplayTreeNode<T>(key,NULL,NULL)) == NULL)
return ; // 插入节点
mRoot = insert(mRoot, z);
// 将节点(key)旋转为根节点
mRoot = splay(mRoot, key);
} /*
* 删除结点(节点的键值为key)，返回根节点
*
* 参数说明：
* tree 伸展树的根结点
* key 待删除结点的键值
* 返回值：
* 根节点
*/
template <class T>
SplayTreeNode<T>* SplayTree<T>::remove(SplayTreeNode<T>* &tree, T key)
{
SplayTreeNode<T> *x; if (tree == NULL)
return NULL; // 查找键值为key的节点，找不到的话直接返回。
if (search(tree, key) == NULL)
return tree; // 将key对应的节点旋转为根节点。
tree = splay(tree, key); if (tree->left != NULL)
{
// 将"tree的前驱节点"旋转为根节点
x = splay(tree->left, key);
// 移除tree节点
x->right = tree->right;
}
else
x = tree->right; delete tree; return x; } template <class T>
void SplayTree<T>::remove(T key)
{
mRoot = remove(mRoot, key);
} /*
* 销毁伸展树
*/
template <class T>
void SplayTree<T>::destroy(SplayTreeNode<T>* &tree)
{
if (tree==NULL)
return ; if (tree->left != NULL)
destroy(tree->left);
if (tree->right != NULL)
destroy(tree->right); delete tree;
} template <class T>
void SplayTree<T>::destroy()
{
destroy(mRoot);
} /*
* 打印"伸展树"
*
* key -- 节点的键值
* direction -- 0，表示该节点是根节点;
* -1，表示该节点是它的父结点的左孩子;
* 1，表示该节点是它的父结点的右孩子。
*/
template <class T>
void SplayTree<T>::print(SplayTreeNode<T>* tree, T key, int direction)
{
if(tree != NULL)
{
if(direction==) // tree是根节点
cout << setw() << tree->key << " is root" << endl;
else // tree是分支节点
cout << setw() << tree->key << " is " << setw() << key << "'s " << setw() << (direction==?"right child" : "left child") << endl; print(tree->left, tree->key, -);
print(tree->right,tree->key, );
}
} template <class T>
void SplayTree<T>::print()
{
if (mRoot != NULL)
print(mRoot, mRoot->key, );
}
#endif
伸展树的测试程序(SplayTreeTest.cpp)
/**
* C++ 语言: 伸展树
*
* @author skywang
* @date 2014/02/03
*/ #include <iostream>
#include "SplayTree.h"
using namespace std; static int arr[]= {,,,,,};
#define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) ) int main()
{
int i,ilen;
SplayTree<int>* tree=new SplayTree<int>(); cout << "== 依次添加: ";
ilen = TBL_SIZE(arr);
for(i=; i<ilen; i++)
{
cout << arr[i] <<" ";
tree->insert(arr[i]);
} cout << "\n== 前序遍历: ";
tree->preOrder(); cout << "\n== 中序遍历: ";
tree->inOrder(); cout << "\n== 后序遍历: ";
tree->postOrder();
cout << endl; cout << "== 最小值: " << tree->minimum() << endl;
cout << "== 最大值: " << tree->maximum() << endl;
cout << "== 树的详细信息: " << endl;
tree->print(); i = ;
cout << "\n== 旋转节点(" << i << ")为根节点";
tree->splay(i);
cout << "\n== 树的详细信息: " << endl;
tree->print(); // 销毁二叉树
tree->destroy(); return ;
}
关于"队列的声明和实现都在头文件中"的原因，是因为队列的实现利用了C++模板，而"C++编译器不能支持对模板的分离式编译"！
伸展树的C++测试程序
伸展树的测试程序运行结果如下：
== 依次添加:
== 前序遍历:
== 中序遍历:
== 后序遍历:
== 最小值:
== 最大值:
== 树的详细信息:
is root
is 's left child
is 's left child
is 's left child
is 's right child
is 's left child == 旋转节点()为根节点
== 树的详细信息:
is root
is 's left child
is 's left child
is 's right child
is 's left child
is 's left child
测试程序的主要流程是：新建伸展树，然后向伸展树中依次插入10,50,40,30,20,60。插入完毕这些数据之后，伸展树的节点是60；此时，再旋转节点，使得30成为根节点。
依次插入10,50,40,30,20,60示意图如下：
将30旋转为根节点的示意图如下：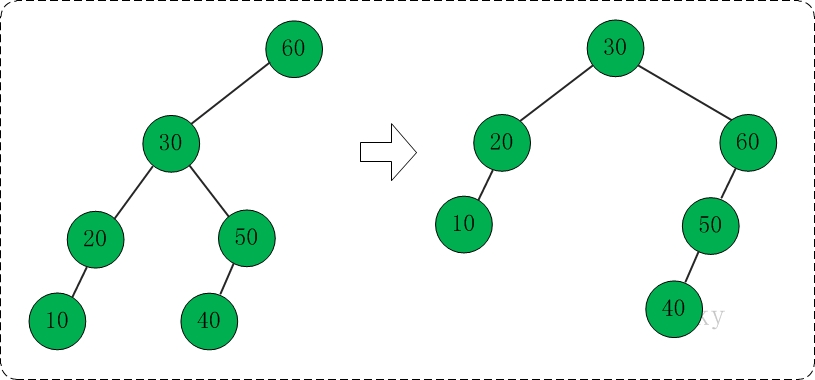
伸展树(二)之 C++的实现的更多相关文章
- 伸展树(一)之 图文解析 和 C语言的实现
概要 本章介绍伸展树.它和"二叉查找树"和"AVL树"一样,都是特殊的二叉树.在了解了"二叉查找树"和"AVL树"之后, ...
- 伸展树(三)之 Java的实现
概要 前面分别通过C和C++实现了伸展树,本章给出伸展树的Java版本.基本算法和原理都与前两章一样.1. 伸展树的介绍2. 伸展树的Java实现(完整源码)3. 伸展树的Java测试程序 转载请注明 ...
- 数据结构（二） --- 伸展树（Splay Tree）
文章图片和代码来自邓俊辉老师课件 概述 伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在O(log n)内完成插入.查找和删除操作.它由丹尼尔·斯立特Daniel Sleator ...
- Splay伸展树学习笔记
Splay伸展树 有篇Splay入门必看文章 —— CSDN链接 经典引文 空间效率:O(n) 时间效率:O(log n)插入.查找.删除 创造者:Daniel Sleator 和 Robert Ta ...
- 纸上谈兵：伸展树（splay tree）
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明.谢谢! 我们讨论过,树的搜索效率与树的深度有关.二叉搜索树的深度可能为n,这种情况下,每次 ...
- [转] Splay Tree(伸展树)
好久没写过了,比赛的时候就调了一个小时,差点悲剧,重新复习一下,觉得这个写的很不错.转自:here Splay Tree(伸展树) 二叉查找树(Binary Search Tree)能够支持多种动态集 ...
- PHP算法 《树形结构》 之 伸展树(1) - 基本概念
伸展树的介绍 1.出处:http://dongxicheng.org/structure/splay-tree/ A. 概述 二叉查找树(Binary Search Tree,也叫二叉排序树,即Bin ...
- 【BBST 之伸展树 (Splay Tree)】
最近“hiho一下”出了平衡树专题,这周的Splay一直出现RE,应该删除操作指针没处理好,还没找出原因. 不过其他操作运行正常,尝试用它写了一道之前用set做的平衡树的题http://codefor ...
- [SinGuLaRiTy] SplayTree 伸展树
[SinGuLaRiTy-1010]Copyrights (c) SinGuLaRiTy 2017. All Rights Reserved. Some Method Are Reprinted Fr ...
随机推荐
- Android：改变Activity切换方式（转载）
overridePendingTransition(enterAnim, exitAnim); Intent intent =new Intent(this,item2.class); startAc ...
- 如何在安装程序中判断操作系统是否是64位 inno
[Setup]; 开启64位模式ArchitecturesInstallIn64BitMode=x64 [Run] ;根据是否是64位进行不同的操作Filename: "..."; ...
- 【转】Xcode 6制作动态及静态Framework
http://years.im/Home/Article/detail/id/52.html 创建iOS动态库 新建工程并选择默认Target为Cocoa Touch Framework, 如图: 做 ...
- mysql触发器_begin end 执行多次语句
//多SQL中导出的触发器语句: DROP TRIGGER IF EXISTS `t_trig`; DELIMITER // CREATE TRIGGER `t_trig` BEFORE INSERT ...
- IE11企业模式介绍及可用性评估
什么是企业模式? 企业模式是可以在 Windows 8.1 和 Windows7 设备上的 Internet Explorer 11 上运行的一种兼容性模式,该模式允许网站使用已修改的浏览器配置来呈现 ...
- IOS越狱开发之——进程通讯
Mac OS下的IPC方式种类很多,大约有下面几种. 1. Mach API 2. CFMessagePort 3. Distributed Objects (DO) 4. Apple events ...
- 通过Typings为Visual Studio Code增强智能提示功能
缘起 最近在学习Node.js及ThinkJS这个框架,用vscode作为开发环境.默认情况下vscode对ThinkJS的代码提示并不好,所以研究了一下,原来可以同通过Typings来让vscode ...
- WPF 设置程序开机自动运行(+注册表项)
#region 设置程序开机自动运行(+注册表项) RegistryKey rgkRun = Registry.LocalMachine.OpenSubKey("SOFTWARE\\Micr ...
- git删除远程文件夹或文件的方法
由于本地修改了文件夹大全名大小写的原因,同步到git上并不区分大小写,造成了一些文件同步不了,所以要先把git远程库上文件夹删除掉,然后再重新同步 如下,我把src里的全部移除,但是本地文件还保留. ...
- java&postgresql时区总结
介绍这篇文章之前,首先回答一个问题,以前都没有时区的概念,程序也写的好好的,为什么要计算时区哪?举个例子,比如有一个订单的时间是:2015-07-04 11:28:19,那么咋一看没什么问题,可是如果 ...