最长回文子串（Manacher算法）

回文字符串，想必大家不会不熟悉吧？

回文串会求的吧？暴力一遍O（n^2)很简单，但当字符长度很长时便会TLE，简单，hash+二分搞定，其复杂度约为O（nlogn), 而Manacher算法能够在线性的时间内处理出最长回文子串。

让我们来看道题：http://acm.hdu.edu.cn/showproblem.php?pid=3068

这个算法的巧妙之处，便是把奇数的回文串和偶数的回文串统一起来考虑了。这一点一直是在做回文串问题中时比较烦的地方。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性，避免了大量不必要的重复匹配。那怎么去实现呢？

我们要求字符串s中最长的回文子串

Manacher重新构造了一个新数组，在每两个字符中间插入一个'#',如下图：

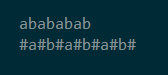
我们很容易发现，如果出现这种情况（如下图）在处理第三个字符（'#'）市，会发现扫到左侧时候可能会出现越界

为了避免索引数超出数组边界值做字符比较，可以在处理过的字符串的第一个位置(索引为0的位置)加入一个区分字符，笔者喜欢用'@'。

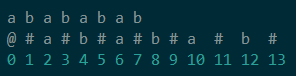
上图便是处理过的样子。（编号表示数组位数，3表示是s[3]的字符）

我们现在用p[i]数组表示以字符s[i]为中心的回文半径（如p[3] = 1)。

我们很容易发现最长子序列的长度刚好是（p[i] - 1)。

那么我们怎么来求p[i]数组呢？

步骤如下：

当处理到[i]的时候，我们去找0-i中是否存在一个数（设为id)使得p[id] + id > i，设mx = p[id] + id。

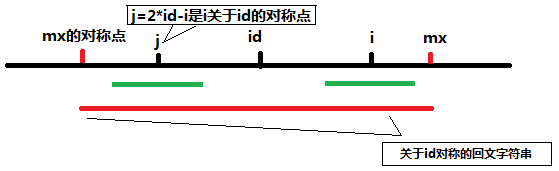
如上图，由于红的字符串是回文字符串，所以关于j对称的回文子串和关于i对称的回文子串是完全一样的(图中两段绿色的线条)，而满足mx-i>P[j]时说明此时j的回文子串半径小于j到mx关于j对称的左端点的差，此时可以初始化P[i]=P[j]。但如果绿色部分超出id的回文串呢？

如下图：

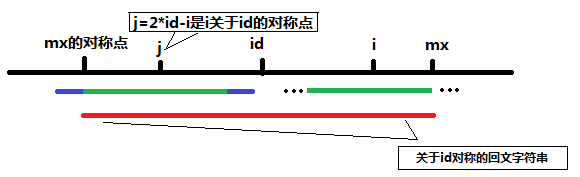
紫色表示以j为中心的回文串超出以id为中心的回文半径的部分（即图中红色部分）由于红的字符串是回文字符串，所以关于j对称的回文子串和关于i对称的在mx和mx的对称点之间的回文子串是完全一样的(图中两段绿色的线条)，而满足mx-i<=P[j]时说明此时j的回文子串半径大于或等于j到mx关于j对称的左端点的差，此时可以初始化P[i]=mx-i，超出部分只能一个个判断。再对P[i]的回文子串半径进行进一步的增大。(以上两图均取自参考论文）

综上所述初始化p[i] = min(p[j], mx - i);

对于超出回文字符串部分（即红色部分，我们只能一个一个的去判断）

即while(s[i + p[i]] == s[i - p[i]])p[i] += 1;

当mx <= i 的时候我们只能将p[i] 初始化为1(对于它都是未知的，只能通过一位一位去比较）。

附上总代码：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 const int N =  + ;

 char s[N];

 int p[N];

 int n, id, mx;

 void work(){
     id = mx = ;
     int ans = ;
     n = strlen(s);
     for(int i = n; i >= ; i --){
         s[ * i + ] = s[i];
         s[ * i + ] = '#';
     }
     s[] = '@';
     p[] = ;
     for(int i = ; i <  * n + ; i ++){
         if(mx > i)p[i] = min(p[ * id - i], mx - i);
         else p[i] = ;
         while(s[i + p[i]] == s[i - p[i]]) p[i] += ;
         if(mx < p[i] + i){
             id = i;
             mx = p[i] + i;
         }
         ans = max(ans, p[i] - );
     }
     printf("%d\n", ans);
 }

 int main(){
     while(scanf("%s", s) == )work();
     return ;
 }

参考资料：http://blog.csdn.net/pi9nc/article/details/9251455