浅谈压缩感知（二十八）：压缩感知重构算法之广义正交匹配追踪(gOMP)

主要内容：

1. gOMP的算法流程
2. gOMP的MATLAB实现
3. 一维信号的实验与结果
4. 稀疏度K与重构成功概率关系的实验与结果

一、gOMP的算法流程

广义正交匹配追踪(Generalized OMP, gOMP)算法可以看作为OMP算法的一种推广。OMP每次只选择与残差相关最大的一个，而gOMP则是简单地选择最大的S个。之所以这里表述为"简单地选择"是相比于ROMP之类算法的，不进行任何其它处理，只是选择最大的S个而已。

gOMP的算法流程：

二、gOMP的MATLAB实现(CS_gOMP.m)

function [ theta ] = CS_gOMP( y,A,K,S )
%   CS_gOMP
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%    y = Phi*Psi * theta
%   令 A = Phi*Psi, 则y=A*theta
%   现在已知y和A，求theta
%   Reference: Jian Wang, Seokbeop Kwon, Byonghyo Shim.  Generalized
%   orthogonal matching pursuit, IEEE Transactions on Signal Processing,
%   vol. , no. , pp. -, Dec. .
%   Available at: http://islab.snu.ac.kr/paper/tsp_gOMP.pdf
    if nargin <
        S = round(max(K/, ));
    end
    [y_rows,y_columns] = size(y);
    if y_rows<y_columns
        y = y';%y should be a column vector
    end
    [M,N] = size(A);%传感矩阵A为M*N矩阵
    theta = zeros(N,);%用来存储恢复的theta(列向量)
    Pos_theta = [];%用来迭代过程中存储A被选择的列序号
    r_n = y;%初始化残差(residual)为y
    for ii=:K%迭代K次，K为稀疏度
        product = A'*r_n;%传感矩阵A各列与残差的内积
        [val,pos]=sort(abs(product),'descend');%降序排列
        Sk = union(Pos_theta,pos(:S));%选出最大的S个
        if length(Sk)==length(Pos_theta)
            if ii ==
                theta_ls = ;
            end
            break;
        end
        if length(Sk)>M
            if ii ==
                theta_ls = ;
            end
            break;
        end
        At = A(:,Sk);%将A的这几列组成矩阵At
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
        %At*theta_ls是y在At)列空间上的正交投影
        r_n = y - At*theta_ls;%更新残差
        Pos_theta = Sk;
        if norm(r_n)<1e-
            break;%quit the iteration
        end
    end
    theta(Pos_theta)=theta_ls;%恢复出的theta
end

三、一维信号的实验与结果

%压缩感知重构算法测试
clear all;close all;clc;
M = ;%观测值个数
N = ;%信号x的长度
K = ;%信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,);
x(Index_K(:K)) = *randn(K,);%x为K稀疏的，且位置是随机的
Psi = eye(N);%x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N)/sqrt(M);%测量矩阵为高斯矩阵
A = Phi * Psi;%传感矩阵
y = Phi * x;%得到观测向量y

%% 恢复重构信号x
tic
theta = CS_gOMP( y,A,K);
x_r = Psi * theta;% x=Psi * theta
toc

%% 绘图
figure;
plot(x_r,'k.-');%绘出x的恢复信号
hold on;
plot(x,'r');%绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x)%恢复残差

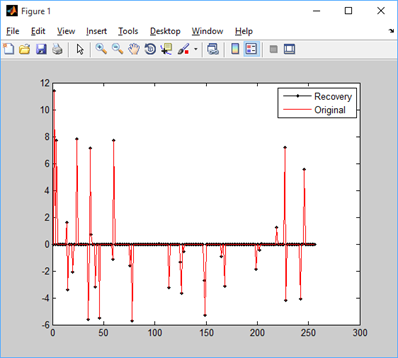
四、稀疏数K与重构成功概率关系的实验与结果

%   压缩感知重构算法测试CS_Reconstuction_KtoPercentagegOMP.m
%   Reference: Jian Wang, Seokbeop Kwon, Byonghyo Shim.  Generalized
%   orthogonal matching pursuit, IEEE Transactions on Signal Processing,
%   vol. , no. , pp. -, Dec. .
%   Available at: http://islab.snu.ac.kr/paper/tsp_gOMP.pdf

clear all;close all;clc;
addpath(genpath('../../OMP/'))

%% 参数配置初始化
CNT = ; %对于每组(K,M,N)，重复迭代次数
N = ; %信号x的长度
Psi = eye(N); %x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
M_set = []; %测量值集合
KIND = ['OMP      ';'ROMP     ';'StOMP    ';'SP       ';'CoSaMP   ';...
    'gOMP(s=3)';'gOMP(s=6)';'gOMP(s=9)'];
Percentage = zeros(N,length(M_set),size(KIND,)); %存储恢复成功概率

%% 主循环，遍历每组(K,M,N)
tic
for mm = :length(M_set)
    M = M_set(mm); %本次测量值个数
    K_set = ::; %信号x的稀疏度K没必要全部遍历，每隔5测试一个就可以了
    %存储此测量值M下不同K的恢复成功概率
    PercentageM = zeros(size(KIND,),length(K_set));
    for kk = :length(K_set)
       K = K_set(kk); %本次信号x的稀疏度K
       P = zeros(,size(KIND,));
       fprintf('M=%d,K=%d\n',M,K);
       for cnt = :CNT  %每个观测值个数均运行CNT次
            Index_K = randperm(N);
            x = zeros(N,);
            x(Index_K(:K)) = *randn(K,); %x为K稀疏的，且位置是随机的
            Phi = randn(M,N)/sqrt(M); %测量矩阵为高斯矩阵
            A = Phi * Psi; %传感矩阵
            y = Phi * x; %得到观测向量y
            %()OMP
            theta = CS_OMP(y,A,K); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()ROMP
            theta = CS_ROMP(y,A,K); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()StOMP
            theta = CS_StOMP(y,A); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()SP
            theta = CS_SP(y,A,K); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()CoSaMP
            theta = CS_CoSaMP(y,A,K); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()gOMP,S=
            theta = CS_gOMP(y,A,K,); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()gOMP,S=
            theta = CS_gOMP(y,A,K,); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
            %()gOMP,S=
            theta = CS_gOMP(y,A,K,); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P() = P() + ;
            end
       end
       for iii = :size(KIND,)
           PercentageM(iii,kk) = P(iii)/CNT*; %计算恢复概率
       end
    end
    for jjj = :size(KIND,)
        Percentage(:length(K_set),mm,jjj) = PercentageM(jjj,:);
    end
end
toc
save KtoPercentage1000gOMP %运行一次不容易，把变量全部存储下来

%% 绘图
S = ['-ks';'-ko';'-yd';'-gv';'-b*';'-r.';'-rx';'-r+'];
figure;
for mm = :length(M_set)
    M = M_set(mm);
    K_set = ::;
    L_Kset = length(K_set);
    for ii = :size(KIND,)
        plot(K_set,Percentage(:L_Kset,mm,ii),S(ii,:)); %绘出x的恢复信号
        hold on;
    end
end
hold off;
xlim([ ]);
legend('OMP','ROMP','StOMP','SP','CoSaMP',...
    'gOMP(s=3)','gOMP(s=6)','gOMP(s=9)');
xlabel('Sparsity level K');
ylabel('The Probability of Exact Reconstruction');
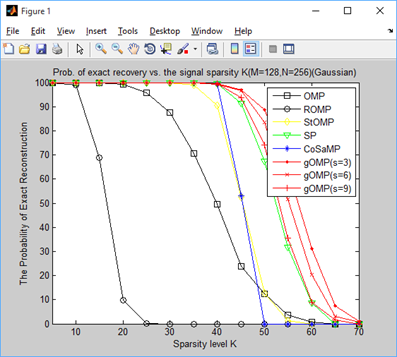
title('Prob. of exact recovery vs. the signal sparsity K(M=128,N=256)(Gaussian)');

结论：gOMP只是在OMP基础上修改了一下原子选择的个数，效果就好很多。

六、参考文章

http://blog.csdn.net/jbb0523/article/details/45693027