KL散度
摘自:
https://www.jianshu.com/p/43318a3dc715?from=timeline&isappinstalled=0
一、解决的问题
量化两种概率分布P和Q可以使用KL散度来度量。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息。
二、公式以及推导
1、信息熵的公式
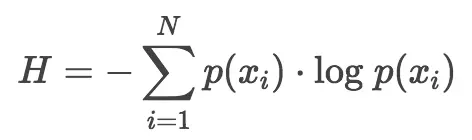
2、KL散度公式
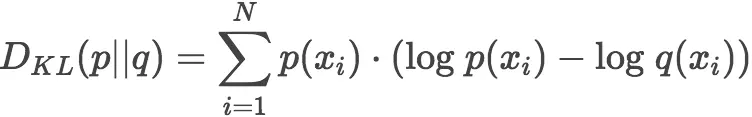
根据上面公式可得,KL散度是近似分布和原始分布对数差的期望值
另一种表示方式:

3、KL散度并非对称
Dkl (Observed || Binomial) != Dkl (Binomial || Observed)
KL散度的更多相关文章
- 【原】浅谈KL散度(相对熵)在用户画像中的应用
最近做用户画像,用到了KL散度,发现效果还是不错的,现跟大家分享一下,为了文章的易读性,不具体讲公式的计算,主要讲应用,不过公式也不复杂,具体可以看链接. 首先先介绍一下KL散度是啥.KL散度全称Ku ...
- PRML读书会第十章 Approximate Inference(近似推断,变分推断,KL散度,平均场, Mean Field )
主讲人 戴玮 (新浪微博: @戴玮_CASIA) Wilbur_中博(1954123) 20:02:04 我们在前面看到,概率推断的核心任务就是计算某分布下的某个函数的期望.或者计算边缘概率分布.条件 ...
- paper 23 :Kullback–Leibler divergence KL散度(2)
Kullback–Leibler divergence KL散度 In probability theory and information theory, the Kullback–Leibler ...
- 浅谈KL散度
一.第一种理解 相对熵(relative entropy)又称为KL散度(Kullback–Leibler divergence,简称KLD),信息散度(information divergence) ...
- 非负矩阵分解(1):准则函数及KL散度
作者:桂. 时间:2017-04-06 12:29:26 链接:http://www.cnblogs.com/xingshansi/p/6672908.html 声明:欢迎被转载,不过记得注明出处哦 ...
- 【机器学习基础】熵、KL散度、交叉熵
熵(entropy).KL 散度(Kullback-Leibler (KL) divergence)和交叉熵(cross-entropy)在机器学习的很多地方会用到.比如在决策树模型使用信息增益来选择 ...
- KL散度、JS散度、Wasserstein距离
1. KL散度 KL散度又称为相对熵,信息散度,信息增益.KL散度是是两个概率分布 $P$ 和 $Q$ 之间差别的非对称性的度量. KL散度是用来 度量使用基于 $Q$ 的编码来编码来自 $P$ 的 ...
- 深度学习中交叉熵和KL散度和最大似然估计之间的关系
机器学习的面试题中经常会被问到交叉熵(cross entropy)和最大似然估计(MLE)或者KL散度有什么关系,查了一些资料发现优化这3个东西其实是等价的. 熵和交叉熵 提到交叉熵就需要了解下信息论 ...
- 机器学习:Kullback-Leibler Divergence (KL 散度)
今天,我们介绍机器学习里非常常用的一个概念,KL 散度,这是一个用来衡量两个概率分布的相似性的一个度量指标.我们知道,现实世界里的任何观察都可以看成表示成信息和数据,一般来说,我们无法获取数据的总体, ...
随机推荐
- centos7 搭建ntp时钟服务器
服务器 : 192.168.137.3 客户机: 192.168.137.6 1. 服务器端 centos7下首先确认服务器的防火墙.selinux关闭状态 # cat /etc/redhat-re ...
- kernel笔记——内核编译与进程管理
内核与操作系统 由于一些商业操作系统设计上的缺陷以及日益庞杂,“操作系统”的概念对很多人而言变得含糊不清.在进一步讨论Linux内核的话题前,我们先区分“内核”与“操作系统”这两个概念. 操作系统:指 ...
- 数据库的设计:深入理解 Realm 的多线程处理机制
你已经阅读过 Realm 关于线程的基础知识.你已经知道了在处理多线程的时候你不需要关心太多东西了,因为强大的 Realm 会帮你处理好这些,但是你还是很想知道更多细节…… 你想知道在 Realm 的 ...
- 【转】从源码分析Handler的postDelayed为什么可以延时?
版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.net/aliankg/article/details/70842494Thread/Hander/Loope ...
- C# PDF转Image图片
概述 PDF是常用的文件格式之一,通常情况下,我们可以使用itextsharp生产PDF文件:可是如何将PDF文件转换成图片那?目前常用的: 思路1.根据PDF绘画轨迹重新绘制图片: 思路2.是将PD ...
- nginx 编译参数详解(运维必看--转)
nginx参数: –prefix= 指向安装目录 –sbin-path 指向(执行)程序文件(nginx) –conf-path= 指向配置文件(nginx.conf) –error-log-path ...
- 近期学习docker遇到的一些问题
最近看某谷的springboot视频,看到了docker部分,在实践过程中遇到了一些问题 默认国外镜像,下载软件很慢 linux内核版本过低,与docker运行不匹配 这里记录一下解决方案 第一个问题 ...
- UIAutomator简介
简介 Android 4.3发布的时候包含了一种新的测试工具–uiautomator,uiautomator是用来做UI测试的.也就是普通的手工测试,点击每个控件元素 看看输出的结果是否符合预期.比如 ...
- 洛谷P1188PASTE题解
题目 这个题主要是一个考分类讨论的模拟题,做这个提的时候首先要脑子清醒,才可以清楚地写出怎么模拟来. \(Code\) #include <iostream> #include <a ...
- zookeeper在windows及linux(含多节点)环境下安装及其命令使用
zookeeper下载 下载url:http://www.apache.org/dyn/closer.cgi/zookeeper/ windows下安装zookeeper 解压到D盘 创建logs目录 ...
