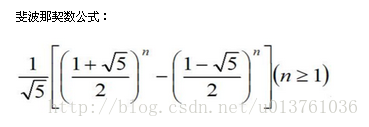hdu1568斐波那契前4位
题意:
就是求斐波那契数,但是只要求输出前四位,(n<=100000000)。
思路:
这个要用到斐波那契的公式和一些log的规律,直接打看着很乱,直接在网上偷张图片吧:
然后就是一些log的性质
log10(a^b) = b * log10(a),log10(a*b) = log10(a) + log10(b)
我们可以根据这个把大数的前几位拿出来,这样:
log10(1234567890)
= log10(1.234567890 * 10^9)
= log10(1.234567890) + 9
这样我们就得到了一个"小数部分"bit = log10(1.234567890)
然后pow(10.0 ,bit) = 1.234567890
这样我们就得到了一个大数的科学技术法的前边部分,想要四位,直接*1000取整就行了。
#include<stdio.h>
#include<math.h>
int num[25];
void ini()
{
num[0] = 0 ,num[1] = 1;
for(int i = 2 ;i <= 20 ;i ++)
num[i] = num[i-1] + num[i-2]; } int main ()
{
ini();
int n;
while(~scanf("%d" ,&n))
{
if(n <= 20)
{
printf("%d\n" ,num[n]);
continue;
}
double now = -0.5 * log10 (5.0) + n * 1.0 * log10((1+sqrt(5.0))/2.0);
double bit = now - (int)now;
double a = pow(10.0,bit);
a *= 1000;
printf("%d\n" ,int(a));
}
return 0;
}
hdu1568斐波那契前4位的更多相关文章
- hdu3117 斐波那契前后4位
题意: 求斐波那契的前后4位,n <= 10^8. 思路: 至于前四位,和hdu1568的求法一样: http://blog.csdn.net/u013761 ...
- AcWing 1303. 斐波那契前 n 项和
输出斐波那契数列前 n 项和 对m取摸的结果 #include<bits/stdc++.h> #define LL long long #define N 3 using namespac ...
- HDU 1568 快速求斐波那契前四位
思路: 把斐波那契通项公式转化成log的形式,高中数学... //By SiriusRen #include <bits/stdc++.h> using namespace std; ], ...
- HDU1568斐波那契推理
Fibonacci Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total S ...
- The sum - SGU 122(斐波那契前N项和)
直接上代码....... ======================================================================================= ...
- HDU 1568 Fibonacci【求斐波那契数的前4位/递推式】
Fibonacci Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Proble ...
- hdu1568&&hdu3117 求斐波那契数前四位和后四位
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1568 题意:如标题所示,求斐波那契数前四位,不足四位直接输出答案 斐波那契数列通式: 当n<=2 ...
- Python基础(二):斐波那契数列、模拟cp操作、生成8位随机密码
一.斐波那契数列 目标: 编写fib.py脚本,主要要求如下: 输出具有10个数字的斐波那契数列 使用for循环和range函数完成 改进程序,要求用户输入一个数字,可以生成用户需要长度的斐波那契数列 ...
- hdu 2160 母猪的故事(睡前随机水一发)(斐波那契数列)
解题思路: 一只母猪生下第二头后立马被杀掉,可以这样想即,生下第二头便被杀掉,可以看成母猪数量没变 第一天 1 第二天 2 第三天 3 :第一头生第二头后杀掉还是1头,第二头再加上第二头生下的,一共三 ...
随机推荐
- Kafka SASL ACL配置踩坑总结
源起:工程现阶段中间件采用的是kafka.满足了大数据的高吞吐,项目间的解耦合,也增强了工程的容错率与扩展性.但是在安全这一块还有漏洞,kafka集群中,只要网站内的任何人知道kafka集群的ip与t ...
- 漏洞复现-ActiveMq任意文件写入漏洞(CVE-2016-3088)
0x00 实验环境 攻击机:Win 10 靶机也可作为攻击机:Ubuntu18 (docker搭建的vulhub靶场) 0x01 影响版本 未禁用PUT.MOVE等高危方法的ActiveM ...
- redis过期key监听事件
目录 redis安装 docker拉取 启动 redis 配置 命令监听 问题 程序监听 具体监听类 效果 总结 redis常用语缓存操作,但是redis功能不仅仅于此.今天我们来看看redis的ke ...
- freebsd root 登录 KDE SDDM
sddm.conf 文件现在默认不会自动生成了.需要自己创建:ee /usr/local/etc/sddm.conf写入MinimumUid=0MaximumUid=00就是root用户.然后更改/u ...
- apktool 回编译报错:No resource identifier found for attribute 'xxxxxx' in package 'android' W:
C:\xxxx\app-release\res\layout-v26\xxxx.xml:5: error: No resource identifier found for attribute 'xx ...
- java中的String,StringBuffer与StringBuilder
String类是不可变类,即一旦一个String对象被创建以后,包含在这个对象中的字符序列是不可改变的,直至这个对象被销毁. StringBuffer对象则代表一个字符序列可变的字符串,当一个Stri ...
- 11、Spring教程之声明式事务
1.回顾事务 事务在项目开发过程非常重要,涉及到数据的一致性的问题,不容马虎! 事务管理是企业级应用程序开发中必备技术,用来确保数据的完整性和一致性. 事务就是把一系列的动作当成一个独立的工作单元,这 ...
- Java 并发工具类 CountDownLatch、CyclicBarrier、Semaphore、Exchanger
本文部分摘自<Java 并发编程的艺术> CountDownLatch CountDownLatch 允许一个或多个线程等待其他线程完成操作.假设现有一个需求:我们需要解析一个 Excel ...
- Android Studio 如何运行单个activity
•写在前面 调试界面运行单个 Activity 可节省编译整个项目的时间提高效率: 本着提高效率的角度,特地上网百度相关知识: •解决方法 首先,在 AndroidManifest.xml 文件中,找 ...
- 17. vue-route详细介绍
前后端路由的来历 前端如何实现页面跳转但是不刷新? 了解hash和history两种方法 vue-router基本使用 安装vue-router 搭建vue-router框架的步骤 vue-route ...