算法：第一节课Master定理

1、ctex：要求用Tex编辑器进行作业的书写

2、与东大本科有差距，还需要多点努力才行。

3、

4、考试不考概念

5、

6、时间复杂度和空间复杂度

7、算法好坏的评价标准

8、基本运算

9、时间复杂度

10、第二章：重要的来了

11、

12、

13、

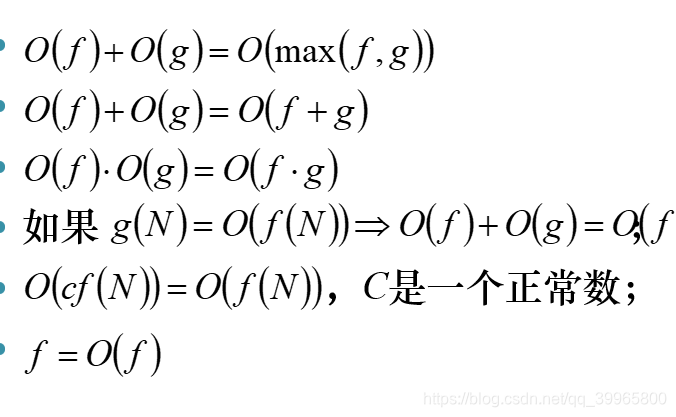
假设矩阵A为n*m，矩阵B为m*n ,则AxB计算时，A矩阵的第一行的第一个元素要进行n次乘法运算，（而不是m次），A矩阵共有 n×m个元素，故总的需要n*m*n次乘法运算。若取 m=n，则时间复杂度为 O(n^3)

14、递归算法的复杂性

15、合并算法讨论

Master定理的解释

是从一个高中生的博客‘借'来的，作为研究生不禁流下惭愧的泪水:(，不废话开始抄:)

正文

介绍master 定理前，首先要知道一个符号

1. T(n) 表示时间复杂度，可以这样表示：T(n)= 一个单项式，例如：

T(n)=2T(n/2)+f(n)

1. Θ 读音：theta，表示等于
2. O 读音：big oh，表示小于等于
3. o 读音：small oh，表示小于
4. Ω 读音：big omega，表示大于等于
5. ω 读音：small omega，表示大于

主定理是怎么表示的呢？

• 我们目前有一个规模为n 的问题
• 通过分治，我们将问题分成a个规模为n/b​，每次递归将带来f(n)f(n) 的额外计算
• 于是得到关系式：

T(n)=aT(b/n​)+f(n)