[刷题] 77 Combinations

要求

• 给出两个整数n和k，在n个数字中选出k个数字的所有组合

示例

• n=4 , k=2
• [ [ 1, 2 ] , [ 1, 3 ] , [ 1, 4 ] , [ 2, 3 ] , [ 2, 4 ] , [ 3, 4 ] ]

思路

实现

• combine()：求解C(n,k)
• generateCombinations()：递归求解
• res：二维向量，保存已经找到的组合
• start：整型，开始搜索的位置
• c：向量，已经找到的组合

 1 class Solution {
 2
 3 private:
 4     vector<vector<int>> res;
 5
 6     // 求解C(n,k)，当前已经找到的组合存在c中，从start开始搜索新元素
 7     void generateCombinations(int n , int k , int start, vector<int> &c){
 8
 9         if( c.size() == k ){
10             res.push_back(c);
11             return;
12         }
13
14         for( int i = start ; i <= n ; i ++ ){
15             c.push_back(i);
16             generateCombinations(n, k, i + 1, c);
17             // 回溯
18             c.pop_back();
19         }
20         return;
21     }
22 public:
23     vector<vector<int>> combine(int n, int k) {
24          res.clear();
25         if( n <= 0 || k <= 0 || k > n)
26             return res;
27         vector<int> c;
28         generateCombinations(n, k, 1, c);
29
30         return res;
31     }
32 };

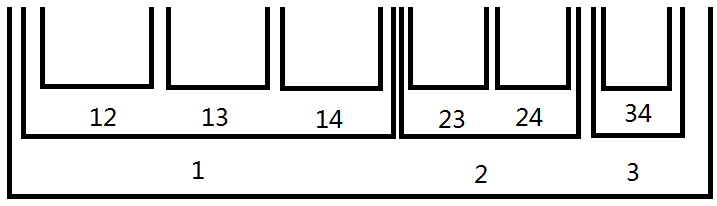
优化

• 剪枝：为递归树剪去不需要搜索的分支
• 如上图中取4的分支
• 当k（递归层数）较大时优化效果明显

 1 class Solution {
 2
 3 private:
 4     vector<vector<int>> res;
 5
 6     // 求解C(n,k)，当前已经找到的组合存在c中，从start开始搜索新元素
 7     void generateCombinations(int n , int k , int start, vector<int> &c){
 8
 9         if( c.size() == k ){
10             res.push_back(c);
11             return;
12         }
13
14         // 进入函数时还有k-c.size()个空位
15         // 所以[i...n]中至少要有k-c.size()个元素
16         // 故i最多为 n - (k-c.size()) + 1
17         for( int i = start ; i <= n - (k-c.size()) + 1 ; i ++ ){
18             c.push_back(i);
19             generateCombinations(n, k, i + 1, c);
20             // 回溯
21             c.pop_back();
22         }
23         return;
24     }
25 public:
26     vector<vector<int>> combine(int n, int k) {
27          res.clear();
28         if( n <= 0 || k <= 0 || k > n)
29             return res;
30         vector<int> c;
31         generateCombinations(n, k, 1, c);
32
33         return res;
34     }
35 };

相关

• 39 Combination Sum
• 40 Combination Sum II
• 216 Combination Sum III
• 78 Subsets
• 90 Subsets II
• 401 Binary Watch