Normalized Cuts and Image Segmentation

目录

• 概
• 主要内容
  • 求解
  • 相似度
  • 总的算法流程
  • skimage.future.graph.cut

Shi J. and Malik J. Normalized cuts and image segmentation. In IEEE Transactions on Pattern Analysis and Machine Intelligence.

概

在Digital Image Preprocessing的书上看到了这个算法, 对于其公式结果的推出不是很理解, 于是下载下来看了看. 本文主要讲的是一种利用图结构进行图像分割的算法.

主要内容

假设\(f(x, y), x=1,2,\cdots M, y=1,2,\cdots N\)为一张图片, 我们想要对其进行分割. 给定某一个距离函数, 可以用于衡量任意两点\(i, j\)的相似度:

\[w_{ij} = w(i, j).
\]

把图片的每一个pixel看成一个节点, pixel和pixel之间的边为一条无向边, 则整体构成了一个无向的图 \(G = (V, E)\), 每条边的权重如上所述是\(w_{ij}\), 故易知\(w_{ij} = w_{ji}\). 我们的目标是将图分成相斥的两块\(A, B\), 即满足:

\[A \bigcup B = V, A \bigcap B = \empty.
\]

以往的做法是, 找到一个分割, 使得下列指标最小:

\[cut(A, B) = \sum_{i \in A, j \in B} w_{ij},
\]

但是这种策略往往会导致不均匀的分割, 即最角落里的元素被单独分割出来:

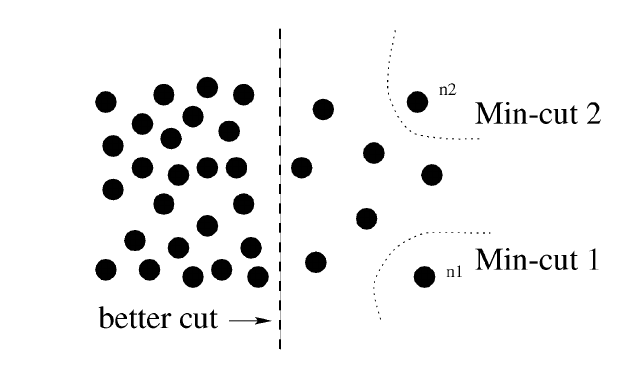
于是作者提出了一种新的指标:

\[Ncut(A, B) = \frac{cut(A, B)}{assoc(A, V)} + \frac{cut(A, B)}{assoc(B, V)},
\]

其中\(assoc(A, V) = \sum_{i \in A, j \in V} w_{ij}\).

注意到:

\[Ncut(A, B) = \frac{cut(A, B)}{cut(A, B) + assoc(A, A)} + \frac{cut(A, B)}{cut(A, B) + assoc(B, B)},
\]

所以只有到\(assoc(A, A), assoc(B, B)\)都足够大的时候Ncut才会足够小, 这说明该指标更关注了内部的一种紧密性.

求解

令

\[x_i = +1, \text{ if } i \in A, \quad x_i = -1 \text{ if } i \in B \\
d_i = \sum_{j}w_{ij}.
\]

则

\[Ncut(A, B) = \frac{\sum_{x_i > 0, x_j < 0} -w_{ij}x_i x_j}{\sum_{x_i > 0}d_i}
+\frac{\sum_{x_i < 0, x_i > 0} -w_{ij}x_i x_j}{\sum_{x_i < 0}d_i}.
\]

容易证明(但是不容易想到):

\[[\frac{1+x}{2}]_i = x_i = +1, \: \text{if } i \in A, \quad
[\frac{1+x}{2}]_i = 0, \: \text{if } i \in B.
\]

\[[\frac{1-x}{2}]_i = -x_i = +1, \: \text{if } i \in B, \quad
[\frac{1-x}{2}]_i = 0, \: \text{if } i \in A.
\]

令

\[[W]_{ij} = w_ij, \\
D_{ii} = d_i,
\]

且\(D_{ii}\)为对角矩阵.

所以我们能够证明以下事实:

\[4\cdot cut(A, B) = (1+x)^T W (1 - x) \\
4 \cdot assoc(A, V) = 2\cdot (1 + x)^T D 1 = (1 + x)^T D (1 + x) \\
4 \cdot assoc(B, V) = 2\cdot (1 - x)^T D 1 = (1 - x)^T D (1 - x) \\
assoc(V, V) = \sum_i d_i = 1^T D 1 \\
(1 + x)^T D (1 - x) = 0.
\]

又注意到:

\[\sum_{x_i > 0, x_j < 0} -w_{ij} x_i x_j = \sum_{x_i > 0} [d_i - \sum_{x_j >0} w_{ij}] = \frac{1}{4}(1 + x)^T (D - W) (1 + x),
\]

于是同理可证:

\[(1 + x)^TW(1 - x) = (1 + x)^T (D - W)(1 +x) = (1 - x)^T (D - W)(1 -x) .
\]

令

\[k = \frac{assoc(A, V)}{assoc(V, V)},
\]

则

\[1 - k = \frac{assoc(B, V)}{assoc(V, V)}.
\]

综上可得:

\[ Ncut(A, B) = \frac{cut(A, B)}{k1^T D1} + \frac{cut(A, B)}{(1-k)1^TD1} = \frac{cut(A, B)}{k(1-k)1^TD1}.
\]

又

\[\begin{array}{ll}
&[(1 + x) - b(1-x)]^T (D-W)[(1+x) - b(1-x)] \\
=& (1+x)^T(D-W)(1+x) + b^2 (1-x)^T(D-W) \\
&- 2b (1+x)^T(D-W)(1-x) \\
=&4(1+b^2)cut(A, B) - 2b (1 + x)^TD(1-x) + 2b(1 + x)^T W(1-x) \\
=&4(1+b^2)cut(A, B) - 0 + 8b cut(A, B) \\
=&4(1 + b)^2 cut(A, B).
\end{array}
\]

又

\[(1 + \frac{k}{1-k})^2 = \frac{1}{(1-k)^2},
\]

故

\[4\cdot Ncut(A,B) = \frac{4(1+b)^2}{b1^TD1} = \frac{[(1 + x) - b(1-x)]^T (D-W)[(1+x) - b(1-x)]}{b1^TD1}, \\
b = \frac{k}{1-k}.
\]

令\(y = (1 + x) - b(1 - x)\), 且

\[y^TDy = \sum_{x_i > 0}d_i + b^2 \sum_{x_i < 0}d_i = b( \sum_{x_i < 0}d_i + b \sum_{x_i < 0}d_i) = b1^TD1.
\]

\[4 \cdot Ncut(A, B) = \frac{y^T(D-W)y}{y^TDy}.
\]

故

\[\min_x Ncut(A, B) = \min_y \frac{1}{4} \frac{y^T(D-W)y}{y^TDy}, \\
\mathrm{s.t.} \quad y_i \in \{1, 1 - b\}.
\]

倘若我们能放松条件至实数域中, 此时只需要通过求解下列系统:

\[(D-W)y = \lambda Dy \Leftrightarrow D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}} z = \lambda z, z = D^{\frac{1}{2}}y.
\]

需要注意的是:

\[(D-W)1 = 0,
\]

此时\(z_0 = D^{\frac{1}{2}}1\),

故\(1\)实际上上述系统的一个解, 且对应最小的特征值, 但其不是我们所要的解. 因为\(y\)必须要还满足:

\[y^T D 1 = \sum_{x_i > 0}d_i - b \sum_{x_i < 0} d_i = 0,
\]

这意味着, 我们要的恰恰是

\[D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}} z = \lambda z, z = D^{\frac{1}{2}}y
\]

的倒数第二小的特征值对应的特征向量\(z_1\), 于是\(y_1 = D^{-\frac{1}{2}}z_1\).

相似度

文中采用如下的计算方式:

\[w_{ij} =
\left \{
\begin{array}{ll}
e^{-\|F_i - F_j\|^2 / \sigma^2_I} \cdot e^{-\|X_i - X_j\|^2 / \sigma^2_X} & \text{if } \|X_i - X_j\| < r \\
0 & \text{else}.
\end{array}
\right.
\]

其中\(F\)对应颜色之类的距离, 如直接取密度值, 而\(X\)对应空间距离, \(r\)限定了搜索范围, 同样会导致\(W\)变成系数矩阵, 对应特征求解加速有帮助.

总的算法流程

1. 计算权重矩阵\(W\)以及\(D\);
2. 通过
   \[D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}} z = \lambda z
   \]

   计算得到倒数第二小的特征值所对应的特征向量\(z_1\)并令\(y_1=z_1\);

3. 通过某种方法(如网格搜索)找到一个阈值\(t\):
   \[x_i = 1, \: \text{if }y_i > t, \: \text{else } -1.
   \]

   且\(x\)的划分下

   \[Ncut(A, B)
   \]

   较小.

4. 对于\(A, B\)可以重复上述分割过程, 直到满足区域数目或者其它某种条件(比如文中说的特征向量的分布过于均匀时停止).

skimage.future.graph.cut

skimage.future.graph.cut